Posted on by Evan Gough

7% of the Stars in the Milky Way’s Center Came From a Single Globular Cluster That Got Too Close and Was Broken Up

The heart of the Milky Way can be a mysterious place. A gigantic black hole resides there, and it’s surrounded by a retinue of stars that astronomers call a Nuclear Star Cluster (NSC). The NSC is one of the densest populations of stars in the Universe. There are about 20 million stars in the innermost 26 light years of the galaxy.

New research shows that about 7% of the stars in the NSC came from a single source: a globular cluster of stars that fell into the Milky Way between 3 and 5 billion years ago.

Humans have been looking up at the gigantic starry arch of the Milky Way since the dawn of our species. But it’s only in the last century or so that astronomers discovered the galactic center. And only in recent decades, aided by the development of adaptive optics and other technologies, has the region begun to surrender its secrets, including the presence of a supermassive black hole.

The center of the Milky Way is still a region of intense astronomical study. Astronomers know that galaxies like the Milky Way grow through mergers with other galaxies, and by enveloping smaller galaxies. The Milky Way is feeding on two of its satellites, the Large and Small Magellanic Clouds. Currently, it’s consuming the gaseous halo that surrounds both dwarf galaxies, but over time, it will eventually take in the dwarf galaxies’ stars, too.

The twin Keck telescopes shooting their laser guide stars into the heart of the Milky Way on a beautifully clear night on the summit on Mauna Kea. Credit: keckobservatory.org/Ethan Tweedie

So it shouldn’t be surprising to find a distinct population of stars in the galactic center that was at one time its own, separate cluster, before being taken in by the Milky Way.

Researchers at multiple institutions around the world are working hard to understand the Milky Way in more detail, including how it grows and evolves over long time periods. Recently, a group of astronomer associated with the European Southern Observatory (ESO) and the Max Planck Institute for Astronomy (MPIA) made some progress. They observed the galactic center with the Very Large Telescope (VLT) and that data has led to some new discoveries. Three teams of researchers have published new papers on different aspects of the galactic center and the newly-discovered population of stars that resides there.

The three studies are:

The galactic center is hard to observe because of the Zone of Avoidance (aka the Zone of Obscuration.) It’s a region so full of dust that it blocks visible light. It takes special instruments and telescopes that see in other wavelengths, especially infrared, to observe it. The VLT in Chile is able to peer into this region.

In “Asymmetric spatial distribution of subsolar metallicity stars in the Milky Way nuclear star cluster,” the team of researchers analyzed the speed, motion, and chemical composition of 700 stars in the galactic center.

Populations of stars aren’t only delineated by the way they move through space together. Their compositions also tell astronomers a lot about their shared origins. Specifically, their metallicity.

This is an image of M80, an ancient globular cluster of stars. Since these stars formed in the early universe, their metallicity content is very low. Image: By NASA, The Hubble Heritage Team, STScI, AURA - Great Images in NASA Description, Public Domain, https://commons.wikimedia.org/w/index.php?curid=6449278
This is an image of M80, an ancient globular cluster of stars. Since these stars formed in the early universe, their metallicity content is very low. Image: By NASA, The Hubble Heritage Team, STScI, AURA – Great Images in NASA Description, Public Domain, https://commons.wikimedia.org/w/index.php?curid=6449278

Stars are made of mostly hydrogen and a little helium. The tiny amounts of elements heavier than those two, which astronomers call metals, reveal a lot about the age and history of the star. It all stems from the early days of the Universe.

Astronomers divide stars into three groups: Population III, Population II, and Population I. Pop III stars are the oldest stars, the first to form in the Universe. At that time, the Universe was 75% hydrogen and about 25% helium, with a tiny fraction of heavier elements Lithium and Beryllium. So that stars that formed at that time have almost nothing heavier in them than helium. They’re called low-metallicity stars.

Pop II stars are not as old, and formed after the first generation of stars. Elements heavier than hygrogen and helium are formed in the hearts of stars, then spread into space when those stars die. Pop II contains some heavier elements than hydrogen and helium, since the previous Pop III stars fused together some heavier elements, or metals, and gave them to the Pop II stars.

An artist's illustration of the Universe's first stars, called Population 3 stars. Pop 3 stars would have been much more massive than most stars today, and would have burned hot and blue. Their lifetimes would've been much shorter than stars like our Sun. There metallicity is also much lower than younger stars. Image Credit: Public Domain, https://commons.wikimedia.org/w/index.php?curid=1582286
An artist’s illustration of the Universe’s first stars, called Population 3 stars. Pop 3 stars would have been much more massive than most stars today, and would have burned hot and blue. Their lifetimes would’ve been much shorter than stars like our Sun. There metallicity is also much lower than younger stars. Image Credit: Public Domain, https://commons.wikimedia.org/w/index.php?curid=1582286

Pop I stars are the younger stars. Our own Sun is one, and since it formed from material generated by the two previous generations of stars, the Sun and the rest of the Pop I stars have more of the heavier elements. They have a higher metallicity.

That’s a fairly rough overview of how it all works. But it shows that metallicity is extremely important to astronomers.

The key to all of this is that if you find a group of stars that are moving in a similar fashion, and if you find that they share the same metallicity, chances are they came from the same cluster and all formed from the same progenitor material. That’s what this research found in the center of the Milky Way.

The majority of stars in the Milky Way’s center share the same composition, or metallicity. They have a higher metallicity than our Sun. But in new research, astronomers identified a sub-group of stars with significantly lower metallicity.

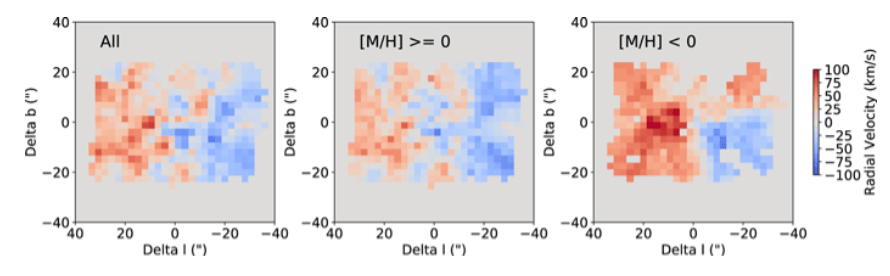
This figure is from one of the three new studies. On the left is the full sample of stars viewed with the KMOS spectrograph on the VLT. The middle shows the radial velocity of stars in the NSC with lower metallicity than the Sun. On the right is the radial velocity of stars with higher metallicity than out Sun. The stars above and below solar metallicity appear to show distinctively different kinematic features. Image Credit: Do et al, 2020.
This figure is from one of the three new studies. On the left is the full sample of stars viewed with the KMOS spectrograph on the VLT. The middle shows the radial velocity of stars in the NSC with lower metallicity than the Sun. On the right is the radial velocity of stars with higher metallicity than out Sun. The stars above and below solar metallicity appear to show distinctively different kinematic features. Image Credit: Do et al, 2020.

About 7% of the stars in the center of the galaxy have this lower metallicity, so they must share an origin. But the question becomes, how did they get there? How did they become part of the same nuclear star cluster (NSC)?

Accepted theory says that these NSCs could, at least partly, form through collisions of smaller clusters of stars over time. These smaller clusters can be grouped inside the larger galaxy, held together by mutual gravity and moving through the galaxy. All galaxies have these clusters.

But eventually, the force of gravity from all the other matter in the galaxy makes these clusters slow down, lose their orbits, and slowly migrate towards the galactic center. Multiple smaller clusters follow this path, and together, they can form the NSC. So this newly discovered sub-population of stars in the NSC could be one of these smaller groups.

That sounds nice and tidy, doesn’t it? But how can this insight be tested? This is where modelling and simulations come in. In a press release, researcher Manuel Arca Sedda said “Among other things, our goal was to find out how long ago such a stellar cluster could have entered the region around the Galactic Centre and where it originally came from.”

In “On the Origin of a Rotating Metal-poor Stellar Population in the Milky Way Nuclear Cluster” the team of researchers ran powerful computer simulations that included the NSC, the supermassive black hole at the center of the galaxy, and a massive star cluster with about one million solar masses. The simulation began with the massive star cluster about 160 light years from the galactic center.

So as a smaller cluster falls into the galactic center, its cohesiveness is gradually diminished over time as it interacts with its surroundings. Some of the stars will be ejected from the group. Once it reaches the center, that disintegration accelerates, and over a relatively short period of time (in astronomical terms) the cluster will become indistinguishable from the larger NSC that it becomes a part of.

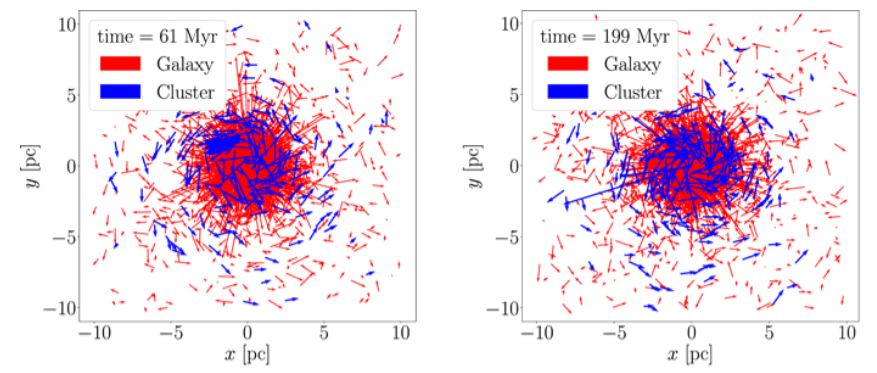
This figure from one of the three new studies shows the velocity vectors of 2% of the simulated stars, or about 21,000 stars, within a 5 parsec sphere centered on the galactic center. The left panel is the simulation at 61 million years, while the right panel is at 199 million years. The red lines represent the velocities and vectors of stars in the Nuclear Stellar Cluster, while blue lines represent those of the newly-identified Stellar Cluster. Before dissolution, the SC is clearly visible in the map in the form of a concentration in the top left region of the NC, and remains recognizable for at least 100 Myr after dissolution. Image Credit: Sedda et al, 2020.
This figure from one of the three new studies shows the velocity vectors of 2% of the simulated stars, or about 21,000 stars, within a 5 parsec sphere centered on the galactic center. The left panel is the simulation at 61 million years, while the right panel is at 199 million years. The red lines represent the velocities and vectors of stars in the Nuclear Stellar Cluster, while blue lines represent those of the newly-identified Stellar Cluster. Before dissolution, the SC is clearly visible in the map in the form of a concentration in the top left region of the NC, and remains recognizable for at least 100 Myr after dissolution. Image Credit: Sedda et al, 2020.

The fact that astronomers have found this group means that it must have fallen into the galactic center in the not-too-distant past. According to the simulations, it’s been in the center and a part of the NSC for between 3 billin and 5 billion years.

Next question? Where did it come from? According to the researchers, there are a couple main possibilities.

It either came from a more distant part of the Milky Way, or it came from outside the galaxy, as a part of a dwarf galaxy. The simulation examined both possibilities, but the results were against the dwarf galaxy as the source.

“Our results indicate that an infall of a rather nearby stellar cluster from the Milky Way itself is more likely,” explains Neumayer. It was probably originally formed about 10,000 to 16,000 light years away.

Fortunately, the researchers were able to test that hypothesis by comparing the group of stars to older globular clusters in the Milky Way and with those that entered the Milky Way in dwarf galaxies. The comparisons showed the newly-discovered cluster of stars had more in common with stars in globular clusters.

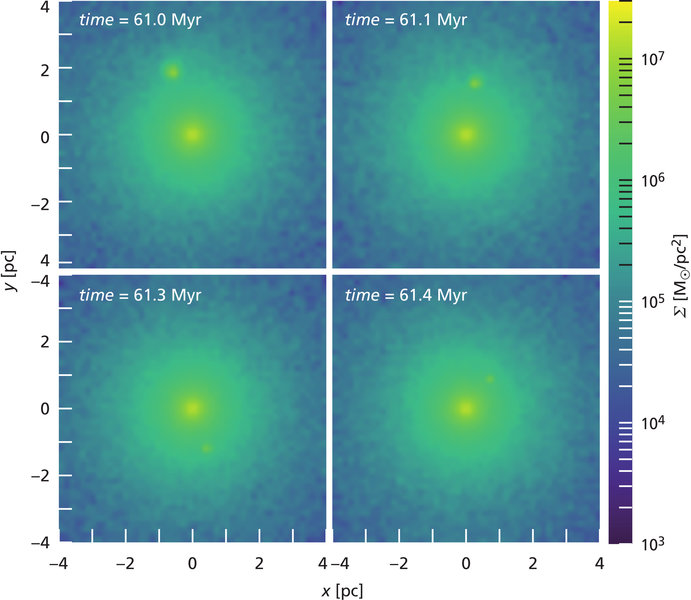
Visualisation of a simulation showing the infall of a globular star cluster into the nuclear star cluster of the Milky Way. The colour scale shows the distribution of star densities along the lines of sight within the Galactic Centre. The globular cluster can be recognised as an isolated point that increasingly merges with the nuclear star cluster over the course of 400 million years and dissolves in the process. Despite the resulting mixing of the two star populations, certain properties of the stars of the globular cluster remain. Image: Manuel Arca Sedda et al. (ARI/ZAH)/MPIA
Visualisation of a simulation showing the infall of a globular star cluster into the nuclear star cluster of the Milky Way. The colour scale shows the distribution of star densities along the lines of sight within the Galactic Centre. The globular cluster can be recognised as an isolated point that increasingly merges with the nuclear star cluster over the course of 400 million years and dissolves in the process. Despite the resulting mixing of the two star populations, certain properties of the stars of the globular cluster remain.
Image: Manuel Arca Sedda et al. (ARI/ZAH)/MPIA

“Although an extragalactic origin of the stars cannot be completely ruled out, it is rather unlikely,” Arca Sedda concluded. “This is an additional sign that the central nuclear star cluster in the galaxy is at least partly the result of the impact of smaller clusters.”

Research like this is revealing the true nature of our celestial home, the Milky Way. For a while, the accepted theory is that massive galaxies like ours grow over time through mergers and accretions. As time goes on and as science progresses, we’re able to point to individual groups of stars and see how and when they joined the family.

It’s like a stellar family tree.

More: