The merger of the Milky Way and Andromeda galaxy won’t happen for another 4 billion years, but the recent discovery of a massive halo of hot gas around Andromeda may mean our galaxies are already touching. University of Notre Dame astrophysicist Nicholas Lehner led a team of scientists using the Hubble Space Telescope to identify an enormous halo of hot, ionized gas at least 2 million light years in diameter surrounding the galaxy.
The Andromeda Galaxy is the largest member of a ragtag collection of some 54 galaxies, including the Milky Way, called the Local Group. With a trillion stars — twice as many as the Milky Way — it shines 25% brighter and can easily be seen with the naked eye from suburban and rural skies.

Think about this for a moment. If the halo extends at least a million light years in our direction, our two galaxies are MUCH closer to touching that previously thought. Granted, we’re only talking halo interactions at first, but the two may be mingling molecules even now if our galaxy is similarly cocooned.
Lehner describes halos as the “gaseous atmospheres of galaxies”. Despite its enormous size, Andromeda’s nimbus is virtually invisible. To find and study the halo, the team sought out quasars, distant star-like objects that radiate tremendous amounts of energy as matter funnels into the supermassive black holes in their cores. The brightest quasar, 3C273 in Virgo, can be seen in a 6-inch telescope! Their brilliant, pinpoint nature make them perfect probes.
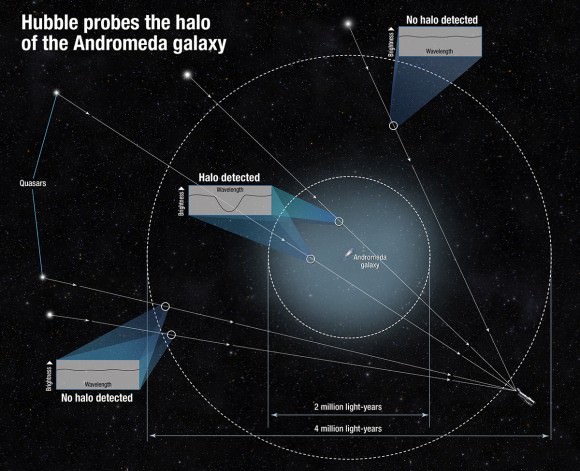
“As the light from the quasars travels toward Hubble, the halo’s gas will absorb some of that light and make the quasar appear a little darker in just a very small wavelength range,” said J. Christopher Howk , associate professor of physics at Notre Dame and co-investigator. “By measuring the dip in brightness, we can tell how much halo gas from M31 there is between us and that quasar.”
Astronomers have observed halos around 44 other galaxies but never one as massive as Andromeda where so many quasars are available to clearly define its extent. The previous 44 were all extremely distant galaxies, with only a single quasar or data point to determine halo size and structure.
Andromeda’s close and huge with lots of quasars peppering its periphery. The team drew from about five years’ worth of observations of archived Hubble data to find many of the 18 objects needed for a good sample.

The halo is estimated to contain half the mass of the stars in the Andromeda galaxy itself, in the form of a hot, diffuse gas. Simulations suggest that it formed at the same time as the rest of the galaxy. Although mostly composed of ionized hydrogen — naked protons and electrons — Andromeda’s aura is also rich in heavier elements, probably supplied by supernovae. They erupt within the visible galaxy and violently blow good stuff like iron, silicon, oxygen and other familiar elements far into space. Over Andromeda’s lifetime, nearly half of all the heavy elements made by its stars have been expelled far beyond the galaxy’s 200,000-light-year-diameter stellar disk.
You might wonder if galactic halos might account for some or much of the still-mysterious dark matter. Probably not. While dark matter still makes up the bulk of the solid material in the universe, astronomers have been trying to account for the lack of visible matter in galaxies as well. Halos now seem a likely contributor.
The next clear night you look up to spy Andromeda, know this: It’s closer than you think!
For more on the topic, here are links to Lehner’s paper in the Astrophysical Journal and the Hubble release.


until I looked at the draft of $7949 , I didnt believe that…my… neighbour was truley earning money part time on their laptop. . there uncle started doing this 4 less than twenty months and a short time ago cleared the mortgage on their villa and purchased a top of the range BMW . Get More Info……………………………http://2.gp/GbUf
Go join your neighbor and their Uncle while we discuss the subject in this article @dilgin.
“You might wonder if galactic halos might account for some or much of the still-mysterious dark matter. Probably not.”
Actually probably so. It’s not just the amount of matter, but also the distance from the center. Dark matter is based on rotational speed. If the objects are larger than we think they are, they’re going to spin faster than they look like they should. Plus we underestimated the size of our own galaxy by 60%. Another strike against dark matter since we use our own galaxy as a baseline to estimate other galaxies.
Alizarin,
I’m referring only to visible matter in galactic halos. This material is not sufficient to account for dark matter’s overwhelming presence.
I’ll agree that halos by themselves don’t account for enough matter to disallow for dark matter.
However, since dark matter was introduced as a possible explanation I’ve never accepted it. Just on the basis of the fact that you want me to believe that there’s an invisible substance so abundant in this universe that it should account for 90% of all matter, yet we can’t detect it, in any fashion except by supposed evidence of its gravity effect. Make a statement like that in any other field of science, and you’ll get the return answer that there’s obviously something wrong with your baseline assumptions that are being made.
altizar,
While it sounds fantastic, the best minds out there not only have shown that there is dark matter – and lots of it – but that it has to exist for galaxies to have formed and gathered into clusters in the first place.
Where from my location in Florida (27d 2′ 38″ N – 82d 14′ 10″ W) would I look in the night sky to see Andromeda?
usnmcb10,
The Andromeda Galaxy is about 20 degrees high in the northeastern sky below and to the right of the W of Cassiopeia just before the start of morning twilight, so around 3:45 a.m. or so. Not a convenient hour but still definitely visible from your location if you know where to look.
“Andromeda’s aura is also rich in heavier elements, probably supplied by supernovae.”
Supernova nucleosynthesis certainly contributes to the observed metal populations. Is this the only source? For example, might not nucleosynthesis via relativistic jets colliding with the inter-stellar medium around a galaxy also add to the observed metal populations in Andromeda’s aura?
TerryG,
I suppose in some galaxies they may contribute to nucleosynthesis, but I’m not aware of large relativistic jets in Andromeda similar to say, M87. I wonder too whether material cast off by red giants as they evolve into white dwarfs might not also make a contribution to heavy elements in the interstellar medium that might ultimately get blown into the halo.
Bob there are Many other great minds on this Earth that do Not Believe in Dark Matter I believe that all the (so called) Missing Mass is inside all the Massive Black holes in the centre of all the Galaxies and we are almost ready to Prove this once and for all…Amen 🙂
Adding hidden mass to the inside of a galaxy would exacerbate the Galaxy rotation curves issues that are solved by the prediction of Dark Matter residing in an outer galactic halo.
It’s fine to have a new theory, so long as it out-perform the current theory.
[img]http://upload.wikimedia.org/wikipedia/commons/thumb/e/ec/M33_rotation_curve_HI.gif/630px-M33_rotation_curve_HI.gif[/img]
Rotation curve of a typical spiral galaxy: predicted (A) and observed (B). Dark matter can explain the ‘flat’ appearance of the velocity curve out to a large radius.
TerryG , Think about this when a Super Super Super Black Hole eats away All its surrounding Galaxy there is only a Black Hole left therefore you cant see it and these hidden Black Holes distributed (Between known Galaxies) Stabalise the Known Cosmos so there is (NO NEED FOR DARK MATTER) but I may be the only one that knows or believes this 🙂 and until proven otherwise is as valid as the rest of the guesswork out there 🙂
UFOs,
I’m sure you’re correct that there are. I’m trying to present what for now is the best if imperfect explanation for all the extra mass we see. Even Fritz Zwicky considered “dark matter” a possibility as long ago as the 1930s. I agree that it’s unsatisfying, but that’s only because we’re at the cusp of understanding its nature.
I believe in “Dark Matter”. The numbers show us there is “something” out there creating the effects we see / observe. Ok, I also don’t like the fact not knowing WHAT creates these effects… not being able to “see them”, explore them but… for starters we gave it a name: “Dark Matter” and, even more weirder… “Dark Energy”. The child has a name despite the fact we know nothing about it but it’s presence / being out there…. somewhere… Hallo…. haaaaallooooooo???
Space has enough space for all matter- seen or unseen. Much has been learned and proven true. You may note that wha man has gleened is just scratching the surface of Universal knowledge.
Unseen matter is known to exist but remains unexplainable despite the effects it has on visible matter.
Space dust, like fog, reflects light to the point it distorts the source. Much of what is considered “Fact” may turn out to be what is unexpected.
Nevertheless, the more we learn, the better it gets.
I have a querie. If the BIG CHILL theory is corect, how come Andromeda and Milky Way are on a collision course ? They should run away one from each other. So this thing (the merge of the galaxyies) has to contradict the big chill theory.
Romeo,
Good question. The reason they don’t run away from each other is that within the Local Group (which is small scale stuff compared to the scale of superclusters) individual galaxies have their own motions. The Local Group is a subunit of the Virgo Supercluster and even larger Laniakea Supercluster that do participate in the overall expansion of the universe.
When they are close enough then gravitational forces are bigger then the dark energy expanding forces the objects still gets pulled towards each other.
There will be a certain distance from an object where the expanding force equals the gravitational force. Any further than that then the expanding forces are bigger than the gravitational forces.
Bob King always gives us Great things to think about and some of the Best Photos I have seen of the Cosmos taken from the ground around his House and around the USA, We all know and appreciate the effort and for Bobs hard work and I know many of your readers thoroughly enjoy and look forward to your next topic. Thanks Again Bob your a true Star 🙂
UFOs,
You’re much too nice. Thank you!
Why can’t dark matter just be space dust. It is matter and dark and no one would say that doesn’t exist. I don’t believe in some new exotic substance that we can’t detect. Also, when Andromeda does fling by maybe we can have a new world that we can hop on before our sun does us in.
Mich48,
I used to wonder the same, but astronomers have accounted for that plus black holes, white dwarfs, brown dwarfs and all kinds of other things made of normal matter. They still don’t add up to anywhere near the amount of mass to account for the rotation curves of galaxies. The current theory of galaxy cluster formation is also based on dark matter serving as “seeding sites” for their formation, too. It seems we can’t escape it … at least for now.