It’s official: on February 11, 10:30 EST, there will be a big press conference about gravitational waves by the people running the gravitational wave detector LIGO. It’s a fair bet that they will announce the first direct detection of gravitational waves, predicted by Albert Einstein 100 years ago. If all goes as the scientists hope, this will be the kick-off for an era of gravitational wave astronomy: for learning about some of the most extreme and violent events in the cosmos by measuring the tiny ripples of space distortions that emanate from them.
Time to brush up on your gravitational wave knowledge, if you haven’t already done so! Here’s a visualization to help you – and we’ll go step by step to see what it means: 
Einstein’s distorted spacetime
In the words of the eminent relativist John Wheeler, Einstein’s theory of general relativity can be summarized in two statements: Matter tells space and time how to curve. And (curved) space and time tell matter how to move. (Here is a slightly longer version on Einstein Online.)
Einstein published the final form of his theory in November 1915. By spring 1916, he had realized another consequence of distorting space and time: general relativity allows for gravitational waves, rhythmic distortions which propagate through space at the speed of light.
For quite some time, physicists weren’t sure whether these gravitational waves were real or a mathematical artifact within Einstein’s theory. (For more about this controversy, see Daniel Kennefick’s book “Traveling at the Speed of Thought and this article.) But since the 1980s, there has been indirect evidence for these waves (which earned its discoverers a Nobel prize, no less, in 1993).
Gravitational waves are emitted by orbiting bodies and certain other accelerated masses. Right now, major international efforts are underway to detect gravitational waves directly. Once detection is possible, the scientists hope to use gravitational waves to “listen” to some of the most violent processes in the universe: merging black holes and/or neutron stars, or the core region of supernova explosions.
Just as regular astronomy uses light and other forms of electromagnetic radiation to learn about distant objects, gravitational wave astronomy will decipher the information contained within gravitational waves. And if you go by recent rumors, gravitational wave astronomy might already have kicked off in mid-September 2015.
What do gravitational waves do?
But what do gravitational waves do? For that, let us look at a simplified, entirely hypothetical situation. (The following are variations on images and animations originally published here on Einstein Online.) Consider particles drifting in space, far from any sources of gravity. Imagine that the particles (red) are arranged in a circle around a center (marked in black): 
If a simple gravitational wave were to pass through this image, coming directly at the reader, distances between these particles would change rhythmically as follows: 
Note the distinctive pattern: When the circle is stretched in the vertical direction, it is compressed in the horizontal direction, and vice versa. That’s typical for gravitational waves (“quadrupole distortion”).
It’s important to keep in mind that this animation, and the ones that will follow, exaggerate the gravitational wave’s effect quite considerably. The gravitational waves detectors such as aLIGO hope to measure are much, much weaker. If our hypothetical circle of particles were as large as the Earth’s orbit around the Sun, a realistic gravitational wave would distort it by less than the diameter of a hydrogen atom.
Gravitational waves moving through space
The animation above shows what could be called a “gravitational oscillation.” To see the whole wave, we need to consider the third dimension.
We talk about a wave when oscillations propagate through space. Consider a water wave: At each point of the surface, we have an oscillation, with the surface rising and falling rhythmically. But it’s only the fact that this oscillation propagates, and that we can see a crest moving over the surface, that makes this into a wave.
It’s the same with gravitational waves. To see that, we will look not at a single circle of freely floating particles, but at many such circles, stacked one behind the other, forming the surface of a cylinder: 
In this image, it’s hard to see which points are in front and which in the back. Let us join each particle to its nearest neighbors with a blue line, and let us also fill out the area between those lines. That way, the geometry is much more obvious: 
Just remember that neither the lines nor the whitish surface is physical. On the contrary, if we want the particles to be maximally susceptible to the effect of the gravitational wave, we should make sure they are truly floating freely, and certainly they shouldn’t be linked in any way!
Now, let us see what the same gravitational wave we saw before does to this assembly of particles. From this perspective, the wave is passing from the right-hand side in the back towards the left-hand side on the front:  As you can see, the wave is propagating through space. For instance, the point where the vertical distances within the circle of particles is maximal is moving towards the observer. The wave nature can be seen even more clearly if we look at this cylinder directly from the side:
As you can see, the wave is propagating through space. For instance, the point where the vertical distances within the circle of particles is maximal is moving towards the observer. The wave nature can be seen even more clearly if we look at this cylinder directly from the side: 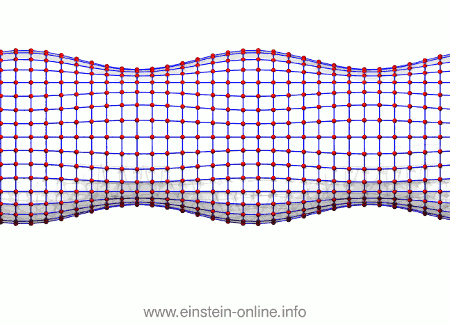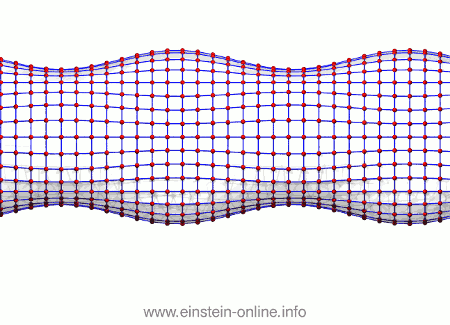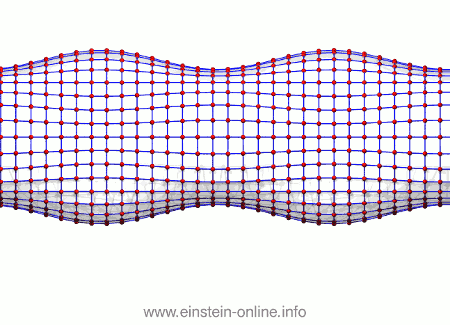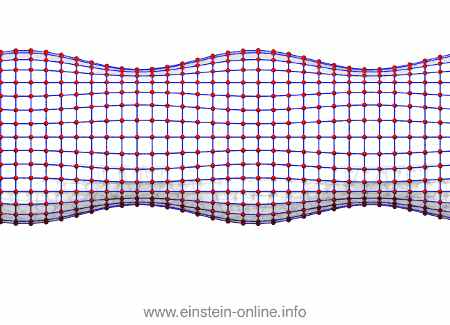
What the animations show is just one kind of simple gravitational wave (“linearly polarized”). Here is another kind (“circularly polarized”): 
This, then, is what the gravitational wave hunters are looking for. Except that they do not have particles floating in free space. Instead, their detectors contain test masses (notably large mirrors) elaborately suspended here on Earth, with laser light to detect the minute distance changes caused by gravitational waves.
More realistic gravitational wave signals, which contain information about merging black holes or the bulk motion of matter inside a supernova explosion, are more complicated still. They combine many simple waves of different frequencies, and the strength of such waves (their amplitude) will change over time in a characteristic fashion.
In these animations, gravitational waves look a bit like wriggling space worms. But these space worms could become the astronomers’ best friends, carrying information about the cosmos that is hard or even impossible to obtain in any other way.
[Don’t miss the sequel: Gravitational wave detectors: how they work]
Update: Gravitational Waves Detected


Very nice explanation. Thank you very much!
You’re welcome! These are exciting times!
General theory of, not theory of general. It is the theory that is general, not the relativity. Shame on you, Universetoday!
Actually, the relativity *is* general. Many more entities are relative/observer dependent in gr than in special relativity!
The Wheeler-DeWitt Equation shows that Time is not real but is a metric, denoting changes in positions in space as charged particles interact — inducing motion. The miniscule mass of the photon, Defined as Zero to simplify atomic mass calculations, is what causes the sun to bend light in the eclipse observations. The recent animations, showing the wave motion of the sun and planets as they rotate around the center of the galaxy, show that the wave motion is a result of gravity.
Sorry, that doesn’t make any sense to me. WdW is quantum gravity, nothing to do with charged particles. Solar light deflection in general relativity is independent of photon mass. And so on.
Electromagnetic waves propagate in a like fashion, with magnetic fields inducing electric fields that in turn induce a new magnetic field, etc., with alternating polarities. I know that gravitational fields don’t have polarities, but is there something mathematically similar at work in gravity wave propagation to the way magnetic fields induce electric fields etc?
There is a way of separating Einstein’s description of gravity into “electric” and “magnetic” parts of gravity, and yes, the mathematics is very similar!
Electromagnetic waves propagate with magnetic fields inducing electric fields that in turn induce a new magnetic field, etc., with alternating polarities. I know that gravitational fields lack polarities, but could there something mathematically similar at work in gravity wave propagation to the way magnetic fields induce electric fields etc?
Try Frame-dragging (and other links in the article): https://en.wikipedia.org/wiki/Frame-dragging
Sorry for the double post. It looks like the submit comment button submitted my comment and them tells me that I have submitted an identical comment. I didn’t see the comment posted, so I edged it and hit the button again with the same result (I should have refreshed the page first!) Anyway, I like the 2nd one better.
This annoying bug happens to me too, every time 🙁
One cool fact about gravitational wave detection: because the observed variable is amplitude (in contrast to nearly every other astronomical observation which detects intensity = amplitude squared), the detection is proportional to 1/distance instead of 1/distance squared. Distant events appear ‘brighter’!
…but whether or not that makes a practical difference depends on how difficult it is to increase the detection limit for amplitudes. 🙂
Geeze, I hope we’re not setting ourselves up for a low sigma? I can see it now… “LISA data may represent the detection of gravity waves but since the detected waves aren’t anything like predicted models we estimate a 25% probability of confirmation. Confirmation will require multiple detections in an extended observation campaign with secondary and tertiary observation platforms now awaiting bugetary approval.”
We’ll know by tomorrow. Personally, I would think that the LIGO (not LISA, btw) people will make very sure their detection meets the usual standards, in terms of sigma or otherwise. 5 sigma minimum is my guess.
Here’s a heads up? I keep getting Word Press ERROR messages… beyond the statement, “Duplicate comment detected; it looks as though you’ve already said that!”
I received the same error message. But the post was successful.
You can learn more about The Big Drag, by contacting me through Facebook. I post about it there, where my friends and esteemed colleagues discuss it. https://www.facebook.com/paul.adamson.965
btw, is there a comment edit feature? I’m committed to the process of revision, and that often applies to my comments, as well as my model. 😀
whoops – that was supposed to go under this comment: http://www.universetoday.com/127255/gravitational-waves-101/#comment-152056
revision needed 😀
The Big Drag Model of the multiverse predicted this elliptical wobble. There are two kinds of gravity, in my model, and the one the produces the wobble, operates from the most fundamental particle’s heart, the “string orbit.” Along with defining gravity in a new way, the model shows that mass is the partial reflection of gravity, and is induced by a reactive process that parallels that of electromagnetic reactance. The mass is acceleration set against acceleration, in the form of eccentricity, in the internal orbit that captures the quantum of phase charge, making it particulate.
http://www.universetoday.com/127255/gravitational-waves-101/#comment-152058
Here’s a link to some information about The Big Drag.
https://www.facebook.com/paul.adamson.965/posts/1243043585722715
Excellent article! How does this impact what we know about Dark Matter? Thanks.