gravitational wave Archives

September 1, 2024September 1, 2024 by Scott Alan Johnston

Gravitational Wave Observatories Could Detect Primordial Black Holes Speeding Through the Solar System

Artist illustration of primordial black holes. NASA's Goddard Space Flight Center

Cosmologists have long hypothesized that the conditions of the early universe could have caused the formation of black holes not long after the Big Bang. These ‘primordial black holes’ have a much wider mass range than those that formed in the later universe from the death of stars, with some even condensed to the width of a single atom.

May 18, 2024May 18, 2024 by Mark Thompson

More Evidence for the Gravitational Wave Background of the Universe

Pulsar timing array. Credit: David Champion/Max Planck

The gravitational wave background was first detected in 2016. It was announced following the release of the first data set from the European Pulsar Timing Array. A second set of data has just been released and, joined by the Indian Pulsar Timing Array, both studies confirm the existence of the background. The latest theory seems to suggest that we’re seeing the combined signal of supermassive black hole mergers.

May 13, 2024May 13, 2024 by Andy Tomaswick

Some Clever Ways to Search for Primordial Black Holes

Primordial Black Holes (PBHs) have recently received much attention in the physics community. One of the primary reasons is the potential link to dark matter. In effect, if PBHs can be proven to exist, there’s a very good chance that they are what dark matter, the invisible thing that makes up 85% of the universe’s mass, is made of. If proven, that would surely be a Nobel-level discovery in astrophysics.

November 25, 2023November 25, 2023 by Brian Koberlein

Dark Matter Could Help Solve the Final Parsec Problem of Black Holes

A simulation of two merging black holes. Credit: Simulating eXtreme Spacetimes (SXS) Project

When galaxies collide, their supermassive black holes enter into a gravitational dance, gradually orbiting each other ever closer until eventually…merging. We know they merge because we see the gravitational beasts that result, and we have detected the gravitational waves they emit as they inspiral. But the details of their final consummation remain a mystery. Now a new paper suggests part of that mystery can be solved with a bit of dark matter.

September 14, 2023September 14, 2023 by Brian Koberlein

If Neutron Stars Have Mountains, They Should Generate Gravitational Waves

Artist's depiction of a highly magnetize neutron star known as a magnetar. Credit: NASA's Goddard Space Flight Center/S. Wiessinger

A neutron star is 2 solar masses compressed into a ball only 12 kilometers wide. Its surface gravity is so immense it compresses atoms and molecules into raw nuclei and squeezes electrons into protons transforming them into neutrons. Given such immense pressures and densities, you might assume neutron stars have an almost perfectly smooth surface. But you’d be wrong because we know that neutron stars can have mountains.

June 18, 2017 by Fraser Cain

Gravitational Astronomy? How Detecting Gravitational Waves Changes Everything

Just a couple of weeks ago, astronomers from Caltech announced their third detection of gravitational waves from the Laser Interferometer Gravitational-Wave Observatory or LIGO.

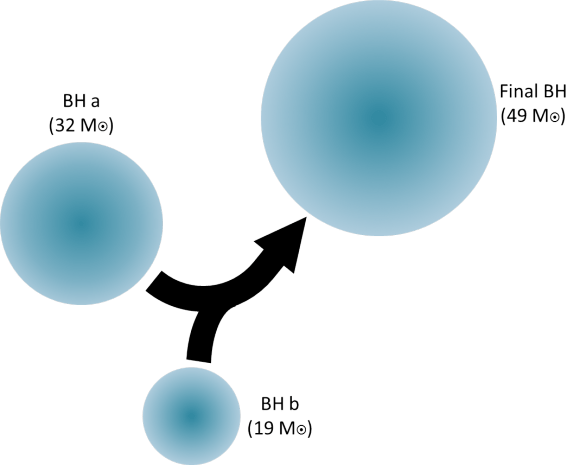
As with the previous two detections, astronomers have determined that the waves were generated when two intermediate-mass black holes slammed into each other, sending out ripples of distorted spacetime.

One black hole had 31.2 times the mass of the Sun, while the other had 19.4 solar masses. The two spiraled inward towards each other, until they merged into a single black hole with 48.7 solar masses. And if you do the math, twice the mass of the Sun was converted into gravitational waves as the black holes merged.

On January 4th, 2017, LIGO detected two black holes merging into one. Courtesy Caltech/MIT/LIGO Laboratory

These gravitational waves traveled outward from the colossal collision at the speed of light, stretching and compressing spacetime like a tsunami wave crossing the ocean until they reached Earth, located about 2.9 billion light-years away.

The waves swept past each of the two LIGO facilities, located in different parts of the United States, stretching the length of carefully calibrated laser measurements. And from this, researchers were able to detect the direction, distance and strength of the original merger.

Seriously, if this isn’t one of the coolest things you’ve ever heard, I’m clearly easily impressed.

Now that the third detection has been made, I think it’s safe to say we’re entering a brand new field of gravitational astronomy. In the coming decades, astronomers will use gravitational waves to peer into regions they could never see before.

Being able to perceive gravitational waves is like getting a whole new sense. It’s like having eyes and then suddenly getting the ability to perceive sound.

This whole new science will take decades to unlock, and we’re just getting started.

As Einstein predicted, any mass moving through space generates ripples in spacetime. When you’re just walking along, you’re actually generating tiny ripples. If you can detect these ripples, you can work backwards to figure out what size of mass made the ripples, what direction it was moving, etc.

Even in places that you couldn’t see in any other way. Let me give you a couple of examples.

Black holes, obviously, are the low hanging fruit. When they’re not actively feeding, they’re completely invisible, only detectable by how they gravitational attract objects or bend light from objects passing behind them.

But seen in gravitational waves, they’re like ships moving across the ocean, leaving ripples of distorted spacetime behind them.

With our current capabilities through LIGO, astronomers can only detect the most massive objects moving at a significant portion of the speed of light. A regular black hole merger doesn’t do the trick – there’s not enough mass. Even a supermassive black hole merger isn’t detectable yet because these mergers seem to happen too slowly.

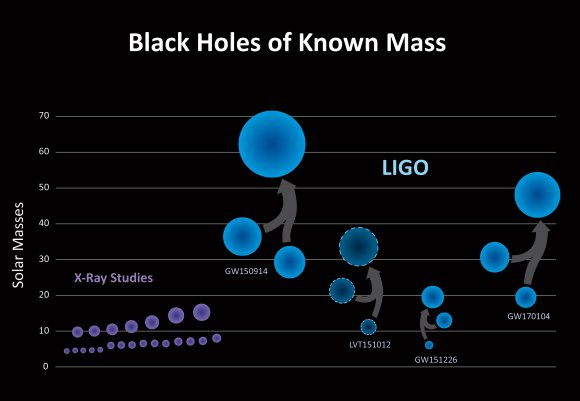
LIGO has already significantly increased the number of black holes with known masses. The observatory has definitively detected two sets of black hole mergers (bright blue). For each event, LIGO determined the individual masses of the black holes before they merged, as well as the mass of the black hole produced by the merger. The black holes shown with a dotted border represent a LIGO candidate event that was too weak to be conclusively claimed as a detection. Credit: LIGO/Caltech/Sonoma State (Aurore Simonnet)

This is why all the detections so far have been intermediate-mass black holes with dozens of times the mass of our Sun. And we can only detect them at the moment that they’re merging together, when they’re generating the most intense gravitational waves.

If we can boost the sensitivity of our gravitational wave detectors, we should be able to spot mergers of less and more massive black holes.

But merging isn’t the only thing they do. Black holes are born when stars with many more times the mass of our Sun collapse in on themselves and explode as supernovae. Some stars, we’ve now learned just implode as black holes, never generating the supernovae, so this process happens entirely hidden from us.

Is there a singularity at the center of a black hole event horizon, or is there something there, some kind of object smaller than a neutron star, but bigger than an infinitely small point? As black holes merge together, we could see beyond the event horizon with gravitational waves, mapping out the invisible region within to get a sense of what’s going on down there.

This illustration shows the merger of two black holes and the gravitational waves that ripple outward as the black holes spiral toward each other. In reality, the area near the black holes would appear highly warped, and the gravitational waves would be difficult to see directly. Credit: LIGO/T. Pyle

We want to know about even less massive objects like neutron stars, which can also form from a supernova explosion. These neutron stars can orbit one another and merge generating some of the most powerful explosions in the Universe: gamma ray bursts. But do neutron stars have surface features? Different densities? Could we detect a wobble in the gravitational waves in the last moments before a merger?

And not everything needs to merge. Sensitive gravitational wave detectors could sense binary objects with a large imbalance, like a black hole or neutron star orbiting around a main sequence star. We could detect future mergers by their gravitational waves.

Are gravitational waves a momentary distortion of spacetime, or do they leave some kind of permanent dent on the Universe that we could trace back? Will we see echoes of gravity from gravitational waves reflecting and refracting through the fabric of the cosmos?

Perhaps the greatest challenge will be using gravitational waves to see beyond the Cosmic Microwave Background Radiation. This region shows us the Universe 380,000 years after the Big Bang, when everything was cool enough for light to move freely through the Universe.

But there was mass there, before that moment. Moving, merging mass that would have generated gravitational waves. As we explained in a previous article, astronomers are working to find the imprint of these gravitational waves on the Cosmic Microwave Background, like an echo, or a shadow. Perhaps there’s a deeper Cosmic Gravitational Background Radiation out there, one which will let us see right to the beginning of time, just moments after the Big Bang.

And as always, there will be the surprises. The discoveries in this new field that nobody ever saw coming. The “that’s funny” moments that take researchers down into whole new fields of discovery, and new insights into how the Universe works.

The Laser Interferometer Gravitational-Wave Observatory (LIGO)facility in Livingston, Louisiana. The other facility is located in Hanford, Washington. Image: LIGO — The Laser Interferometer Gravitational-Wave Observatory (LIGO) facility in Livingston, Louisiana. The other facility is located in Hanford, Washington. Image: LIGO

The LIGO project was begun back in 1994, and the first iteration operated from 2002 to 2012 without a single gravitational wave detection. It was clear that the facility wasn’t sensitive enough, so researchers went back and made massive improvements.

In 2008, they started improving the facility, and in 2015, Advanced LIGO came online with much more sensitivity. With the increased capabilities, Advanced LIGO made its first discovery in 2016, and now two more discoveries have been added.

LIGO can currently only detect the general hemisphere of the sky where a gravitational wave was emitted. And so, LIGO’s next improvement will be to add another facility in India, called INDIGO. In addition to improving the sensitivity of LIGO, this will give astronomers three observations of each event, to precisely detect the origin of the gravitational waves. Then visual astronomers could do follow up observations, to map the event to anything in other wavelengths.

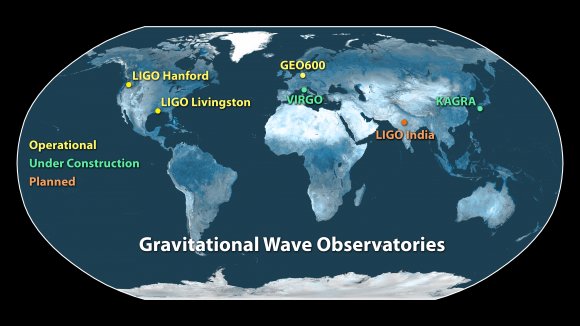
Current operating facilities in the global network include the twin LIGO detectors—in Hanford, Washington, and Livingston, Louisiana—and GEO600 in Germany. The Virgo detector in Italy and the Kamioka Gravitational Wave Detector (KAGRA) in Japan are undergoing upgrades and are expected to begin operations in 2016 and 2018, respectively. A sixth observatory is being planned in India. Having more gravitational-wave observatories around the globe helps scientists pin down the locations and sources of gravitational waves coming from space. Image made in February 2016. Credit: Caltech/MIT/LIGO Lab

A European experiment known as Virgo has been operating for a few years as well, agreeing to collaborate with the LIGO team if any detections are made. So far, the Virgo experiment hasn’t found anything, but it’s being upgraded with 10 times the sensitivity, which should be fully operational by 2018.

A Japanese experiment called the Kamioka Gravitational Wave Detector, or KAGRA, will come online in 2018 as well, and be able to contribute to the observations. It should be capable of detecting binary neutron star mergers out to nearly a billion light-years away.

Just with visual astronomy, there are a set of next generation supergravitational wave telescopes in the works, which should come online in the next few decades.

The Europeans are building the Einstein Telescope, which will have detection arms 10 km long, compared to 4 km for LIGO. That’s like, 6 more km.

There’s the European Space Agency’s space-based Laser Interferometer Space Antenna, or LISA, which could launch in 2030. This will consist of a fleet of 3 spacecraft which will maintain a precise distance of 2.5 million km from each other. Compare that to the Earth-based detection distances, and you can see why the future of observations will come from space.

The Laser Interferometer Space Antenna (LISA) consists of three spacecraft orbiting the sun in a triangular configuration. Credit: NASA

And that last idea, looking right back to the beginning of time could be a possibility with the Big Bang Observer mission, which will have a fleet of 12 spacecraft flying in formation. This is still all in the proposal stage, so no concrete date for if or when they’ll actually fly.

Gravitational wave astronomy is one of the most exciting fields of astronomy. This entirely new sense is pushing out our understanding of the cosmos in entirely new directions, allowing us to see regions we could never even imagine exploring before. I can’t wait to see what happens next.

May 30, 2017 by Fraser Cain

What Was Cosmic Inflation? The Quest to Understand the Earliest Universe

The Big Bang. The discovery that the Universe has been expanding for billions of years is one of the biggest revelations in the history of science. In a single moment, the entire Universe popped into existence, and has been expanding ever since.

We know this because of multiple lines of evidence: the cosmic microwave background radiation, the ratio of elements in the Universe, etc. But the most compelling one is just the simple fact that everything is expanding away from everything else. Which means, that if you run the clock backwards, the Universe was once an extremely hot dense region

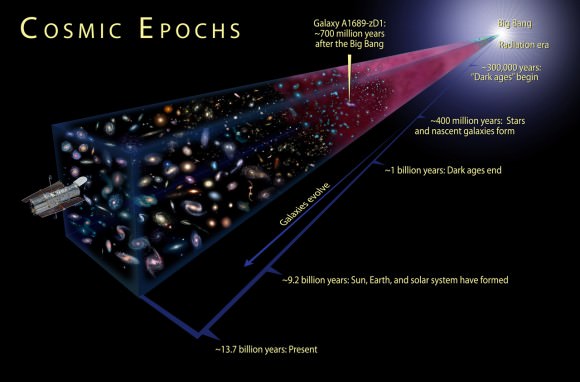
A billion years after the big bang, hydrogen atoms were mysteriously torn apart into a soup of ions. Credit: NASA/ESA/A. Felid (STScI)).

Let’s go backwards in time, billions of years. The closer you get to the Big Bang, the closer everything was, and the hotter it was. When you reach about 380,000 years after the Big Bang, the entire Universe was so hot that all matter was ionized, with atomic nuclei and electrons buzzing around each other.

Keep going backwards, and the entire Universe was the temperature and density of a star, which fused together the primordial helium and other elements that we see to this day.

Continue to the beginning of time, and there was a point where everything was so hot that atoms themselves couldn’t hold together, breaking into their constituent protons and neutrons. Further back still and even atoms break apart into quarks. And before that, it’s just a big question mark. An infinitely dense Universe cosmologists called the singularity.

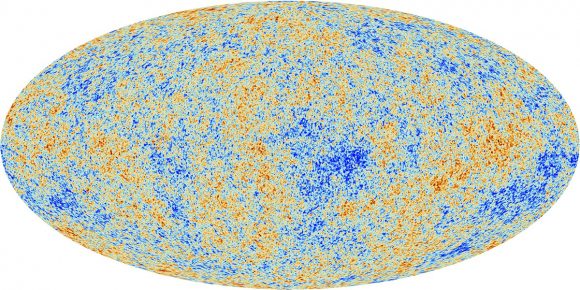
When you look out into the Universe in all directions, you see the cosmic microwave background radiation. That’s that point when the Universe cooled down so that light could travel freely through space.

And the temperature of this radiation is almost exactly the same in all directions that you look. There are tiny tiny variations, detectable only by the most sensitive instruments.

Cosmic microwave background seen by Planck. Credit: ESA

When two things are the same temperature, like a spoon in your coffee, it means that those two things have had an opportunity to interact. The coffee transferred heat to the spoon, and now their temperatures have equalized.

When we see this in opposite sides of the Universe, that means that at some point, in the ancient past, those two regions were touching. That spot where the light left 13.8 billion years ago on your left, was once directly touching that spot on your right that also emitted its light 13.8 billion years ago.

This is a great theory, but there’s a problem: The Universe never had time for those opposite regions to touch. For the Universe to have the uniform temperature we see today, it would have needed to spend enough time mixing together. But it didn’t have enough time, in fact, the Universe didn’t have any time to exchange temperature.

Imagine you dipped that spoon into the coffee and then pulled it out moments later before the heat could transfer, and yet the coffee and spoon are exactly the same temperature. What’s going on?

Alan H. Guth. Credit: Betsy Devine (CC BY-SA 3.0)

To address this problem, the cosmologist Alan Guth proposed the idea of cosmic inflation in 1980. That moments after the Big Bang, the entire Universe expanded dramatically.

And by “moments”, I mean that the inflationary period started when the Universe was only 10^-36 seconds old, and ended when the Universe was 10^-32 seconds old.

And by “expanded dramatically”, I mean that it got 10^26 times larger. That’s a 1 followed by 26 zeroes.

Before inflation, the observable Universe was smaller than an atom. After inflation, it was about 0.88 millimeters. Today, those regions have been stretched 93 billion light-years apart.

This concept of inflation was further developed by cosmologists Andrei Linde, Paul Steinhardt, Andy Albrecht and others.

Inflation resolved some of the shortcomings of the Big Bang Theory.

The first is known as the flatness problem. The most sensitive satellites we have today measure the Universe as flat. Not like a piece-of-paper-flat, but flat in the sense that parallel lines will remain parallel forever as they travel through the Universe. Under the original Big Bang cosmology, you would expect the curvature of the Universe to grow with time.

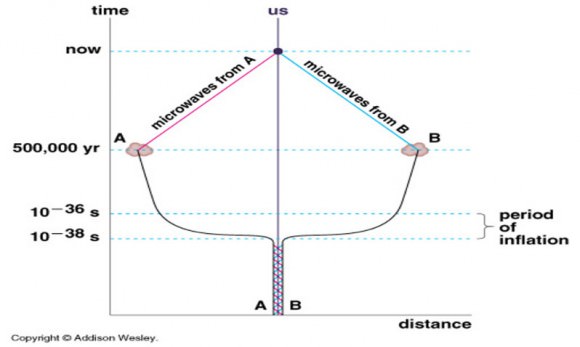
The horizon problem in Big Bang cosmology. How is it that distant parts of the universe possess such similar physical properties? Credit: Addison Wesley.

The second is the horizon problem. And this is the problem I mentioned above, that two regions of the Universe shouldn’t have been able to see each other and interact long enough to be the same temperature.

The third is the monopole problem. According to the original Big Bang theory, there should be a vast number of heavy, stable “monopoles”, or a magnetic particle with only a single pole. Inflation diluted the number of monopoles in the Universe so don’t detect them today.

Although the cosmic microwave background radiation appears mostly even across the sky, there could still be evidence of that inflationary period baked into it.

The Big Bang and primordial gravitational waves. Credit: bicepkeck.org

In order to do this, astronomers have been focusing on searching for primordial gravitational waves. These are different from the gravitational waves generated through the collision of massive objects. Primordial gravitational waves are the echoes from that inflationary period which should be theoretically detectable through the polarization, or orientation, of light in the cosmic microwave background radiation.

A collaboration of scientists used an instrument known as the Background Imaging of Cosmic Extragalactic Polarization (or BICEP2) to search for this polarization, and in 2014, they announced that maybe, just maybe, they had detected it, proving the theory of cosmic inflation was correct.

Unfortunately, another team working with the space-based Planck telescope posted evidence that the fluctuations they saw could be fully explained by intervening dust in the Milky Way.

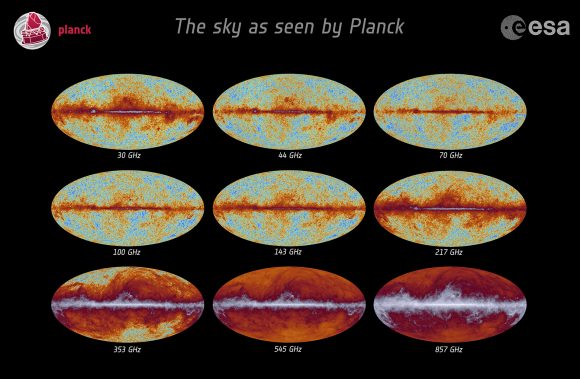
Planck’s view of its nine frequencies. Credit: ESA and the Planck Collaboration

The problem is that BICEP2 and Planck are designed to search for different frequencies. In order to really get to the bottom of this question, more searches need to be done, scanning a series of overlapping frequencies. And that’s in the works now.

BICEP2 and Planck and the newly developed South Pole Telescope as well as some observatories in Chile are all scanning the skies at different frequencies at the same time. Distortion from various types of foreground objects, like dust or radiation should be brighter or dimmer in the different frequencies, while the light from the cosmic microwave background radiation should remain constant throughout.

There are more telescopes, searching more wavelengths of light, searching more of the sky. We could know the answer to this question with more certainty shortly.

One of the most interesting implications of cosmic inflation, if proven, is that our Universe is actually just one in a vast multiverse. While the Universe was undergoing that dramatic expansion, it could have created bubbles of spacetime that spawned other universes, with different laws of physics.

Multiverse Theory — Artist concept of the multiverse. Credit: Florida State University

In fact, the father of inflation, Alan Guth, said, “It’s hard to build models of inflation that don’t lead to a multiverse.”

And so, if inflation does eventually get confirmed, then we’ll have a whole multiverse to search for in the cosmic microwave background radiation.

The Big Bang was one of the greatest theories in the history of science. Although it did have a few problems, cosmic inflation was developed to address them. Although there have been a few false starts, astronomers are now performing a sensitive enough search that they might find evidence of this amazing inflationary period. And then it’ll be Nobel Prizes all around.

February 10, 2016February 11, 2016 by Markus Pössel

Gravitational Wave Detectors: How They Work

It’s official: this Thursday, February 11, at 10:30 EST, there will be parallel press conferences at the National Press Club in Washington, D.C., in Hannover, Germany, and near Pisa in Italy. Not officially confirmed, but highly probable, is that people running the LIGO gravitational wave detectors will announce the first direct detection of a gravitational wave. The first direct detection of minute distortions of spacetime, travelling at the speed of light, first postulated by Albert Einstein almost exactly 100 years ago. Nobel prize time.

Time to brush up on your gravitational wave basics, if you haven’t done so! In Gravitational waves and how they distort space, I had a look at what gravitational waves do. Now, on to the next step: How can we measure what they do? How do gravitational wave detectors such as LIGO work?

Recall that this is how a gravitational wave will change the distances between particles, floating freely in a circular formation in empty space: The wave is moving at right angles to the screen, towards you. I’ve greatly exaggerated the distance changes. For a realistic wave, even the giant distance between the Earth and the Sun would only change by a fraction of the diameter of a hydrogen atom. Tiny changes indeed.

How to detect something like this?

The first unsuccessful attempts to detect gravitational waves in the 1960s tried to measure how they make aluminum cylinders ring like a very soft bell. (Tragic story; Joe Weber [1919-2000], the pioneering physicist behind this, was sure he had detected gravitational waves in this way; after thorough analysis and replication attempts, community consensus emerged that he hadn’t.)

Afterwards, physicists came up with alternative scheme. Imagine that you are replacing the black point in the center of the previous animation with a detector, and the rightmost red particle with a laser light source. Now you send light pulses (represented here by fast red dots) from the light source to the detector; let’s first look at this with the gravitational wave switched off:

Every time a light pulse reaches the detector, an indicator light flashes yellow. The pulses are sent out regularly, they all travel at the same speed, hence they also reach the detector in regular intervals.

If a gravitational wave passes through this system, again from the back and coming towards you, distances will change. Let us keep our camera trained on the detector, so the detector remains where it is. The changing distance to the light source, and also the changing distances between the light pulses, and some of the changes in distance between light pulses and detector or source, are due to the gravitational wave. Here is what that would look like (again, hugely exaggerated):

Keep your eye on the blinking light, and you will see that its blinking is not so regular any more. Sometimes, the light blinks faster, sometimes slower. This is an effect of the gravitational wave. An effect by which we can hope to detect the gravitational wave.

“We” in this case are the radio astronomers working on what are known as Pulsar Timing Arrays. The sender of regular pulses are pulsars, rotating neutron stars sweeping a radio beam across our antennas like a cosmic lighthouse. The detectors are radio telescopes here on Earth. Detection is anything but easy. With a single pulsar, you’d need to track pulse arrival times with an accuracy of a few billionths of a second over half a year, and make sure you are not being fooled by various other sources of timing variations. So far, no gravitational waves have been detected in this way, although the radio astronomers are keeping at it.

To see how gravitational wave detectors like LIGO work, we need to make things a little more complex.

Interferometric gravitational wave detectors: the set-up

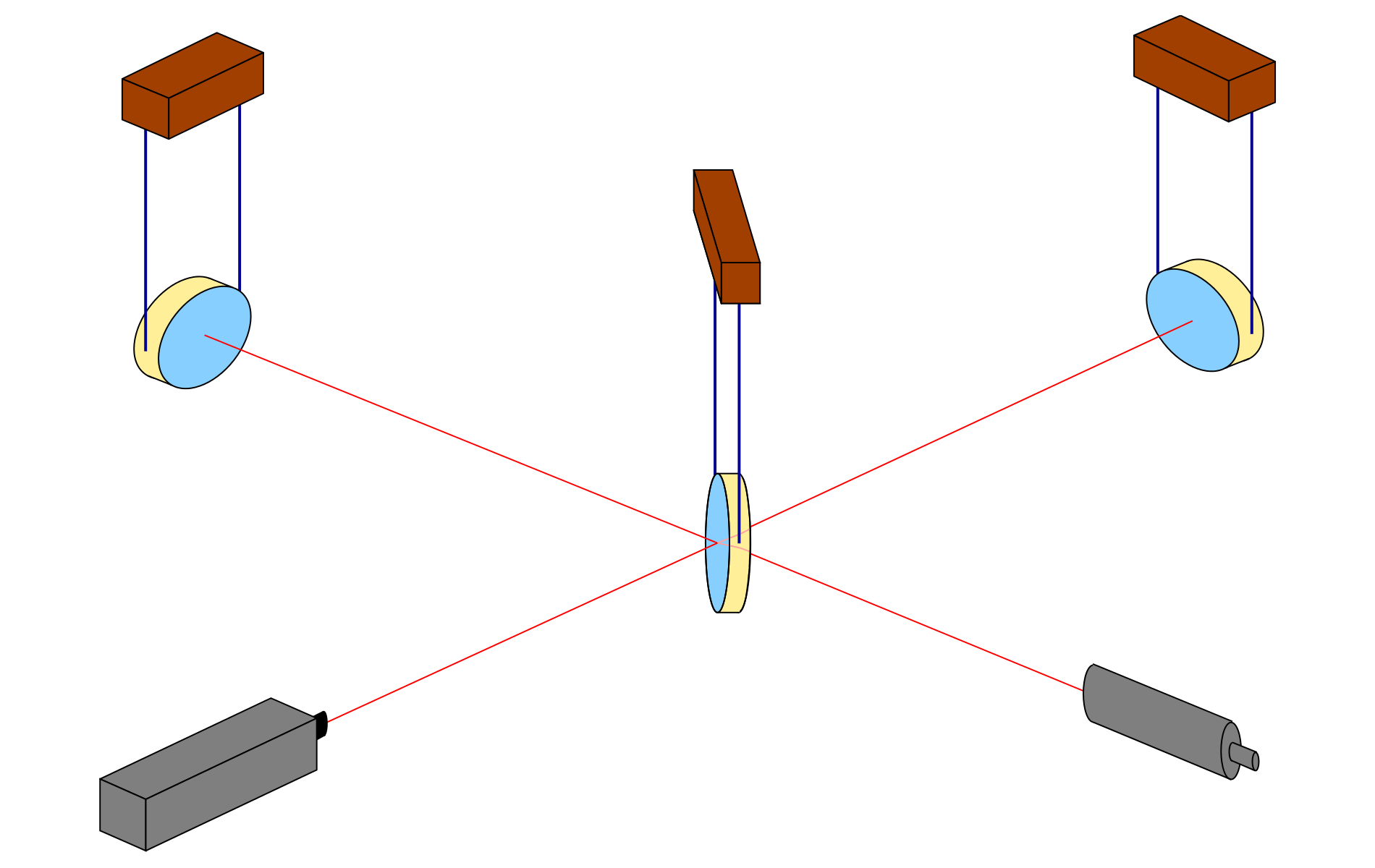
Here is the basic set-up: Two mirrors, a receiver (or “light detector”), a light source and what is known as a beamsplitter: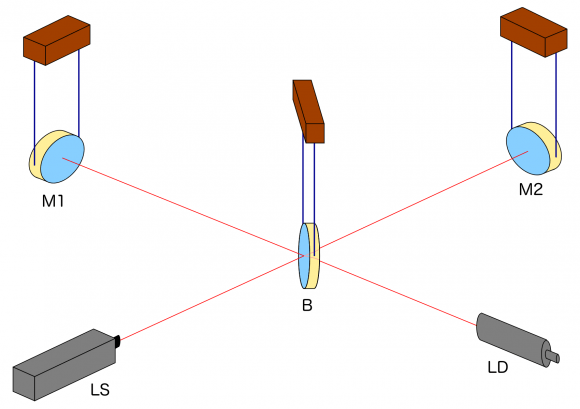

Light is sent into the detector from the (laser) light source LS to the beamsplitter B which, true to its name, sends half of the light on to the mirror M1 and lets the other half through to the mirror M2. At M1 and M2, respectively, the light is reflected back to the beam splitter. There, the light arriving from M1 (or M2) is split again, with half going towards the light detector LD, the other half back in the direction of the light source LS. We will ignore the latter half and pretend, for the sake of our simplified explanation, that all the light reaching B from M1 or M2 goes on to the light detector LD.

(To avoid confusion, I will always refer to LD as the “light detector” and take the unqualified word “detector” to mean the whole setup.)

This setup, by the way, is called a Michelson Interferometer. We’ll see below why it is a good setup for gravitational wave detectors.

In what follows, we will assume that the mirrors and the beam splitter, shown as being suspended, react to the gravitational wave in the same way freely floating particles would react. The key effects are between the mirrors and the beam splitter in what are called the two arms of the detector. Arm length is huge in today’s detectors, running to a few kilometers. In comparison, light source and light detector are very close to the beamsplitter; changes of the distances between these three do not signify.

Light pulses in a gravitational wave detector

Next, let us see how light pulses run through this detector. Here is the same setup, seen from above: 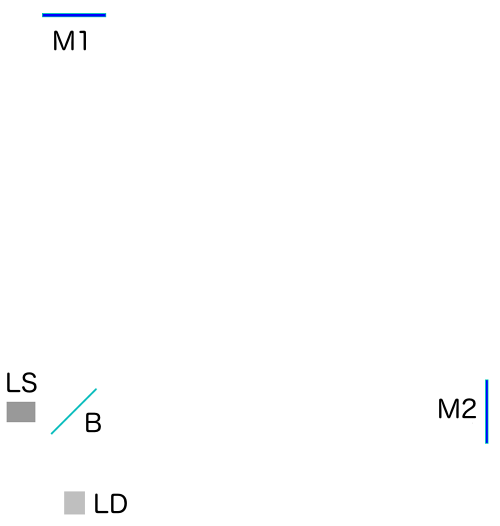Light source LS, the two mirrors M1 and M2, the beamsplitter B and the light detector LD: all present and accounted for.

Next, we let the light source emit light pulses. For greater clarity, I will make two artificial and unrealistic changes. I will send red and green pulses into the detector, representing the light that goes into the horizontal and the vertical arm, respectively. In reality, there is no distinction, just light apportioned at the beamsplitter. Light running towards M1 will be offset a little to the left, light coming back from M1 to the right, for better clarity. Same goes for M2. This, too, is different in a real detector. That said, here come the light pulses: 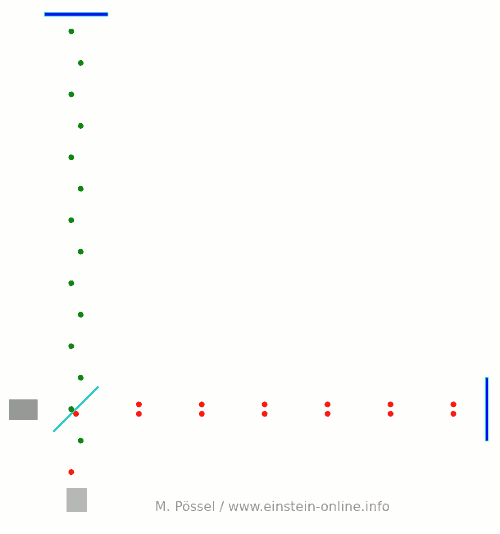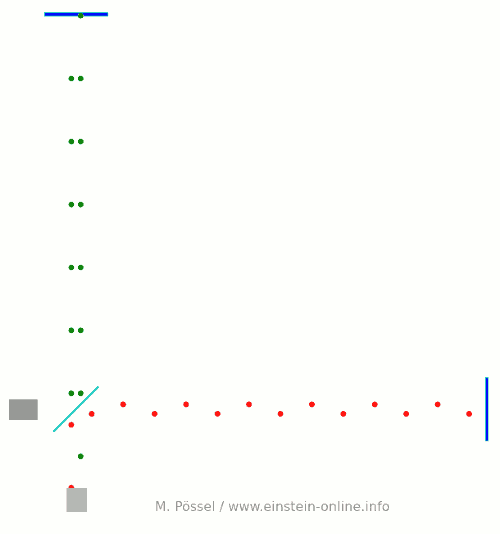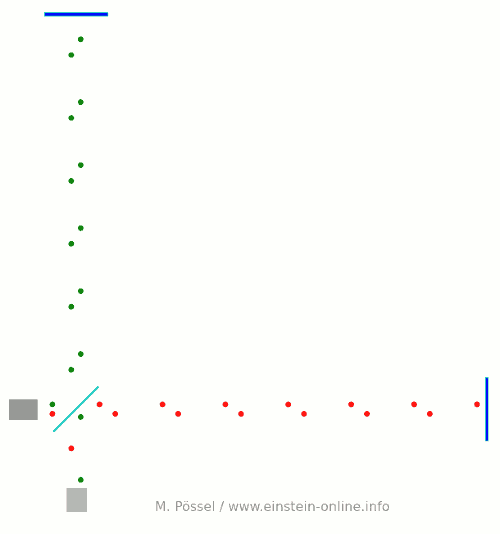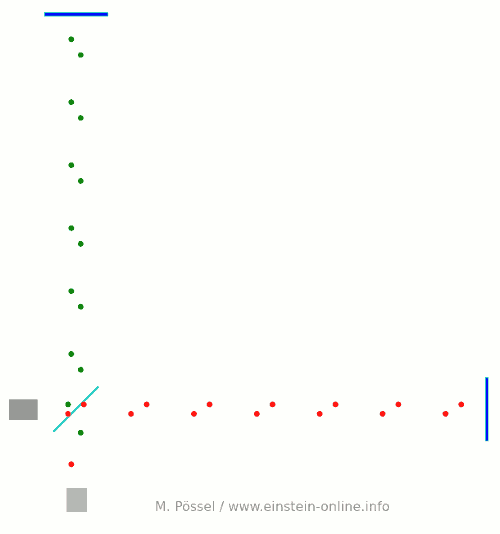Light starts at the light source to the left. Light that has left the source together, travels together (so green and red pulses are side by side) until the beam splitter. The beam splitter then sends the green pulses on their upward journey and lets the red pulses pass on their way towards the mirror on the right. All the particles that arrive back at the beamsplitter after reflection at M1 or M2. At the beamsplitter, they are directed towards the light detector at the bottom.

In this setup, the horizontal arm is slightly longer than the vertical arm. Red particles have to cover some extra distance. That is why they arrive at the detector a bit later, and we get an alternating rhythm: green, red, green, red, with equal distances in between. This will become important later on.

Here is a diagram, a kind of registration strip, which shows the arrival times for red and green pulses at the light detector (time is measured in “animation frames”): The pattern is clear: red and green pulses arrive evenly spaced, one after the other.

Bring on the gravitational wave!

Next, let’s switch on our standard gravitational wave (exaggerated, passing through the screen towards you, and so on). Here is the result: 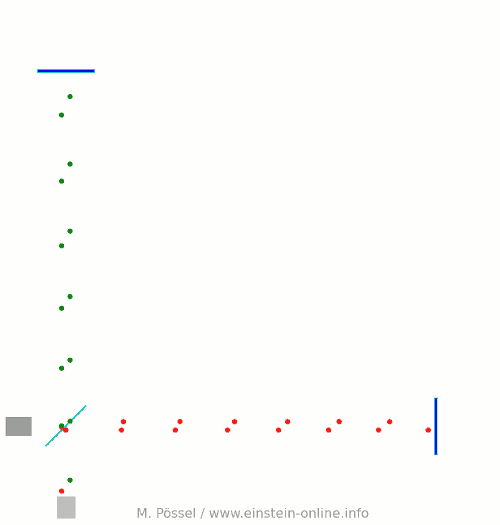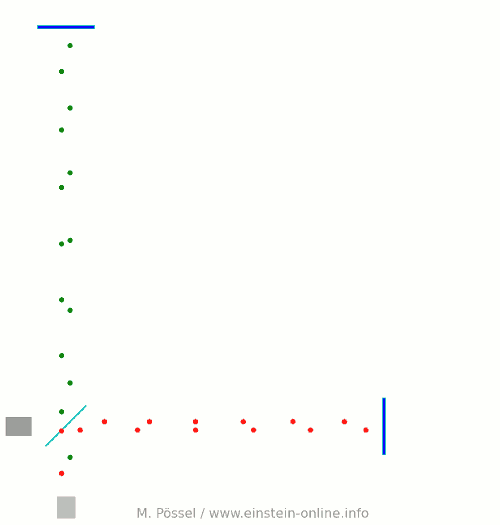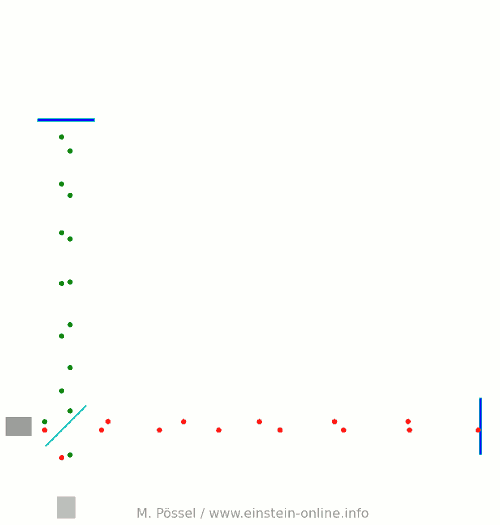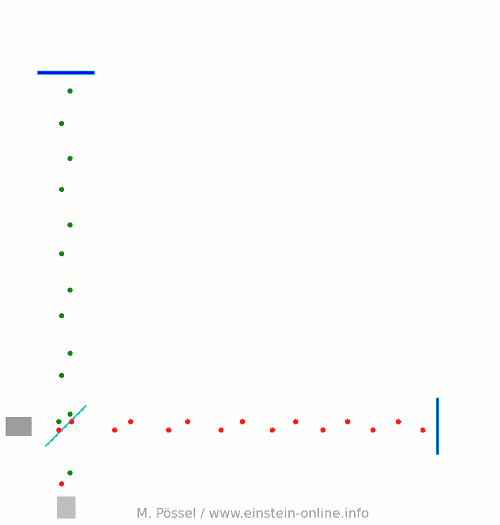We have trained our camera on the beamsplitter (so in our image, the beamsplitter doesn’t move). We ignore any slight changes in distance between beamsplitter and light source/light detector. Instead, we focus on the mirrors M1 and M2, which change their distance from the beamsplitter just as we would expect from the earlier animations.

Look at the way the pulses arrive at our light detector: sometimes red and green are almost evenly spaced, sometimes they close together. That is caused by the gravitational wave. Without the wave, we had strict regularity.

Here is the corresponding “registration strip” diagram. You can see that at some times, the light pulses of each color are closer together, at others, farther apart:

At the time I have marked with a hand-drawn arrow, red and green pulses arrive almost in unison!

The pattern is markedly different from the scenario without a gravitational wave. Detect this change in the pattern, and you have detected the gravitational wave.

Running interference

If you’ve wondered why detectors like LIGO are called interferometric gravitational wave detectors, we will need to think about waves a bit more. If not, let me just state that detectors like LIGO use the wave properties of light to measure the changes in pulse arrival rate you have seen in the last animation. To skip the details, feel free to jump ahead to the last section, “…and now for something a thousand times more complicated.”

Light is a wave, with crests and troughs corresponding to maxima and minima of the electric and of the magnetic field. While the animations I have shown you track the propagation of light pulses, they can also be used to understand what happens to a light wave in the interferometer. Just assume that each of the moving red and green dots in the detector marks the position of a wave crest.

Particles just add up. Take 2 particle and add 2 particles, and you will end up with 4 particles. But if you add up (combine, superimpose) waves, it depends. Sometimes, one wave plus another wave is indeed a bigger wave. Sometimes, it’s a smaller wave, or no wave at all. And sometimes it’s complicated.

When two waves are in perfect sync, the crests of the one aligning with the crests of the other, and the troughs aligning, too, you indeed get a bigger wave. The following diagram shows at which times the different parts of two light waves arrive at the light detector, and how they add up. (I’ve placed a dot on top of each crest; that is what the dots where meant to signify, after all.) 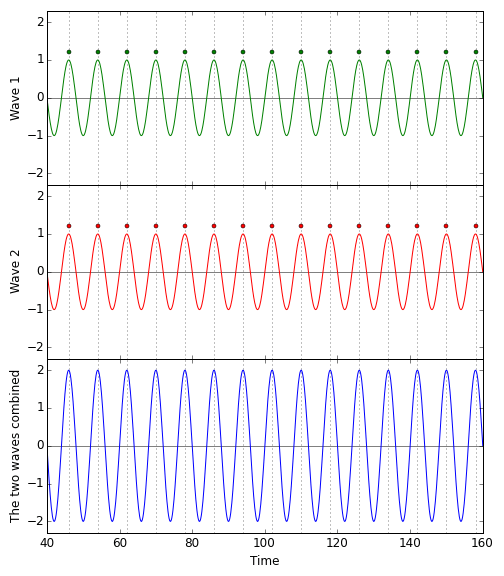On top, the green wave, perfectly aligned with the red wave (which, for clarity, is shown directly below the green wave). Add the two waves up, and you will get the (markedly stronger) blue wave in the bottom panel.

Not so if the two waves are maximally misaligned, the crests of each aligned with the troughs of the other. A crest and a trough cancel each other out. The sum of a wave and a maximally misaligned wave of equal strength is: no wave at all. Here is the corresponding diagram: 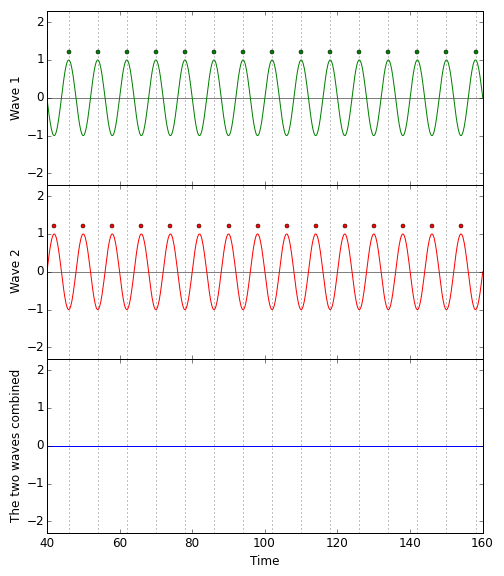Recall that this was exactly the setup for our gravitational wave detector in the absence of gravitational waves: Red and green pulses with equal spacing; troughs of the one wave perfectly aligned with the crests of the other. The result: No light at the light detector. (For realistic gravitational wave detectors, that is almost true.)

When a gravitational wave passes through the detector, the situation changes. Here is the corresponding pattern of pulse/wave crest arrival times for the animation above: 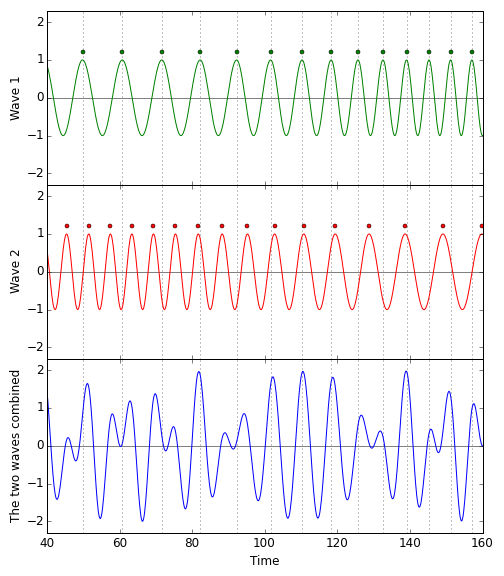The blue pattern, which is the sum of the red and the green, is complex. But it is not a flat line. There is light at the light detector where there was no light before, and the cause of the change is the gravitational wave passing through.

All in all, this makes a (highly simplified) version of how gravitational wave detectors such as LIGO work. Whatever the scientists will report this Thursday, it is based on light signals at the exit of such an interferometric detector.

And now for something a thousand times more complicated

Real gravitational wave detectors are, of course, much more complicated than that. I haven’t even started talking about the many disturbances scientists need to take into account – and to suppress as far as possible. How do you suspend the mirrors so that (at least for certain gravitational waves) they will indeed be influenced as if they were freely floating particles? How do you prevent seismic noise, cars or trains in the wider neighborhood and so on from moving your mirrors a tiny little bit (either by vibrations or by their own gravity)? What about fluctuations of the laser light?

Gravitational wave hunting is largely a hunt for noise, and for ways of suppressing that noise. The LIGO gravitational wave detectors and their kin are highly complex machines, with hundreds of control circuits, highly elaborate mirror suspensions, the most stable lasers known to physics (and some of the most high-powered). The technology has been contributed by numerous group from all over the world.

But all this is taking us too far, and I refer you to the pages of the detectors and collaborations for additional information:

LIGO pages at Caltech

Pages of the LIGO Scientific Collaboration

GEO 600 pages

VIRGO / EGO pages

You can find some further information about gravitational waves on the Einstein Online website:

Einstein Online: Spotlights on gravitational waves

Update: Gravitational Waves Discovered

February 8, 2016February 11, 2016 by Markus Pössel

Gravitational Waves and How They Distort Space

Gravitational waves distort space in a rhythmic fashion. These simple animations show how. — That's not a space worm. It's what a gravitational wave does to space according to Einstein's theory of general relativity.

It’s official: on February 11, 10:30 EST, there will be a big press conference about gravitational waves by the people running the gravitational wave detector LIGO. It’s a fair bet that they will announce the first direct detection of gravitational waves, predicted by Albert Einstein 100 years ago. If all goes as the scientists hope, this will be the kick-off for an era of gravitational wave astronomy: for learning about some of the most extreme and violent events in the cosmos by measuring the tiny ripples of space distortions that emanate from them.

Time to brush up on your gravitational wave knowledge, if you haven’t already done so! Here’s a visualization to help you – and we’ll go step by step to see what it means:

Einstein’s distorted spacetime

In the words of the eminent relativist John Wheeler, Einstein’s theory of general relativity can be summarized in two statements: Matter tells space and time how to curve. And (curved) space and time tell matter how to move. (Here is a slightly longer version on Einstein Online.)

Einstein published the final form of his theory in November 1915. By spring 1916, he had realized another consequence of distorting space and time: general relativity allows for gravitational waves, rhythmic distortions which propagate through space at the speed of light.

For quite some time, physicists weren’t sure whether these gravitational waves were real or a mathematical artifact within Einstein’s theory. (For more about this controversy, see Daniel Kennefick’s book “Traveling at the Speed of Thought and this article.) But since the 1980s, there has been indirect evidence for these waves (which earned its discoverers a Nobel prize, no less, in 1993).

Gravitational waves are emitted by orbiting bodies and certain other accelerated masses. Right now, major international efforts are underway to detect gravitational waves directly. Once detection is possible, the scientists hope to use gravitational waves to “listen” to some of the most violent processes in the universe: merging black holes and/or neutron stars, or the core region of supernova explosions.

Just as regular astronomy uses light and other forms of electromagnetic radiation to learn about distant objects, gravitational wave astronomy will decipher the information contained within gravitational waves. And if you go by recent rumors, gravitational wave astronomy might already have kicked off in mid-September 2015.

What do gravitational waves do?

But what do gravitational waves do? For that, let us look at a simplified, entirely hypothetical situation. (The following are variations on images and animations originally published here on Einstein Online.) Consider particles drifting in space, far from any sources of gravity. Imagine that the particles (red) are arranged in a circle around a center (marked in black):

If a simple gravitational wave were to pass through this image, coming directly at the reader, distances between these particles would change rhythmically as follows:

Note the distinctive pattern: When the circle is stretched in the vertical direction, it is compressed in the horizontal direction, and vice versa. That’s typical for gravitational waves (“quadrupole distortion”).

It’s important to keep in mind that this animation, and the ones that will follow, exaggerate the gravitational wave’s effect quite considerably. The gravitational waves detectors such as aLIGO hope to measure are much, much weaker. If our hypothetical circle of particles were as large as the Earth’s orbit around the Sun, a realistic gravitational wave would distort it by less than the diameter of a hydrogen atom.

Gravitational waves moving through space

The animation above shows what could be called a “gravitational oscillation.” To see the whole wave, we need to consider the third dimension.

We talk about a wave when oscillations propagate through space. Consider a water wave: At each point of the surface, we have an oscillation, with the surface rising and falling rhythmically. But it’s only the fact that this oscillation propagates, and that we can see a crest moving over the surface, that makes this into a wave.

It’s the same with gravitational waves. To see that, we will look not at a single circle of freely floating particles, but at many such circles, stacked one behind the other, forming the surface of a cylinder:

In this image, it’s hard to see which points are in front and which in the back. Let us join each particle to its nearest neighbors with a blue line, and let us also fill out the area between those lines. That way, the geometry is much more obvious:

Just remember that neither the lines nor the whitish surface is physical. On the contrary, if we want the particles to be maximally susceptible to the effect of the gravitational wave, we should make sure they are truly floating freely, and certainly they shouldn’t be linked in any way!

Now, let us see what the same gravitational wave we saw before does to this assembly of particles. From this perspective, the wave is passing from the right-hand side in the back towards the left-hand side on the front: As you can see, the wave is propagating through space. For instance, the point where the vertical distances within the circle of particles is maximal is moving towards the observer. The wave nature can be seen even more clearly if we look at this cylinder directly from the side: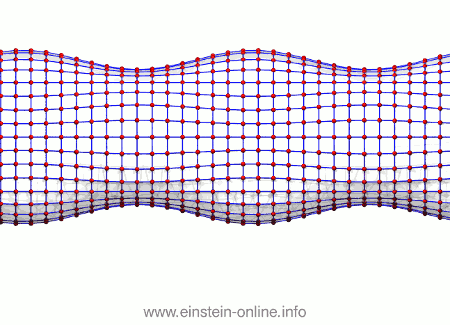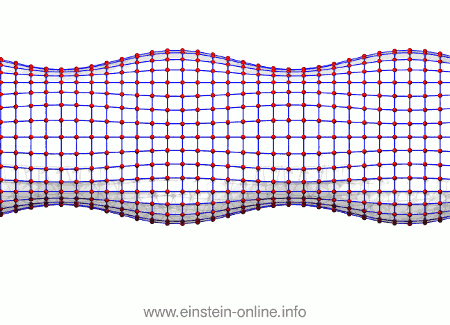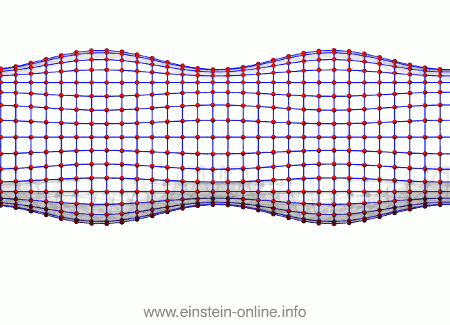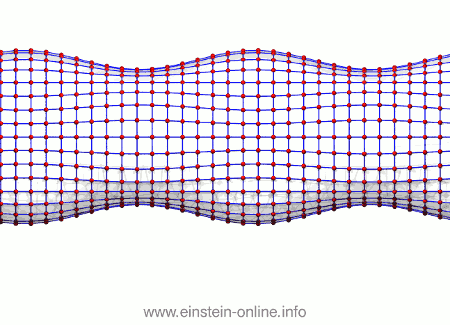

What the animations show is just one kind of simple gravitational wave (“linearly polarized”). Here is another kind (“circularly polarized”):

This, then, is what the gravitational wave hunters are looking for. Except that they do not have particles floating in free space. Instead, their detectors contain test masses (notably large mirrors) elaborately suspended here on Earth, with laser light to detect the minute distance changes caused by gravitational waves.

More realistic gravitational wave signals, which contain information about merging black holes or the bulk motion of matter inside a supernova explosion, are more complicated still. They combine many simple waves of different frequencies, and the strength of such waves (their amplitude) will change over time in a characteristic fashion.

In these animations, gravitational waves look a bit like wriggling space worms. But these space worms could become the astronomers’ best friends, carrying information about the cosmos that is hard or even impossible to obtain in any other way.

[Don’t miss the sequel: Gravitational wave detectors: how they work]

Update: Gravitational Waves Detected

August 29, 2012December 23, 2015 by Jason Major

Effects of Einstein’s Elusive Gravitational Waves Observed

Chandra data (above, graph) on J0806 show that its X-rays vary with a period of 321.5 seconds, or slightly more than five minutes. This implies that the X-ray source is a binary star system where two white dwarf stars are orbiting each other (above, illustration) only 50,000 miles apart, making it one of the smallest known binary orbits in the Galaxy. According to Einstein's General Theory of Relativity, such a system should produce gravitational waves - ripples in space-time - that carry energy away from the system and cause the stars to move closer together. X-ray and optical observations indicate that the orbital period of this system is decreasing by 1.2 milliseconds every year, which means that the stars are moving closer at a rate of 2 feet per year. — Potential stellar collision. Credit: Chandra

Two white dwarfs similar to those in the system SDSS J065133.338+284423.37 spiral together in this illustration from NASA. Credit: D. Berry/NASA GSFC

Locked in a spiraling orbital embrace, the super-dense remains of two dead stars are giving astronomers the evidence needed to confirm one of Einstein’s predictions about the Universe.

A binary system located about 3,000 light-years away, SDSS J065133.338+284423.37 (J0651 for short) contains two white dwarfs orbiting each other rapidly — once every 12.75 minutes. The system was discovered in April 2011, and since then astronomers have had their eyes — and four separate telescopes in locations around the world — on it to see if gravitational effects first predicted by Einstein could be seen.

According to Einstein, space-time is a structure in itself, in which all cosmic objects — planets, stars, galaxies — reside. Every object with mass puts a “dent” in this structure in all dimensions; the more massive an object, the “deeper” the dent. Light energy travels in a straight line, but when it encounters these dents it can dip in and veer off-course, an effect we see from Earth as gravitational lensing.

Einstein also predicted that exceptionally massive, rapidly rotating objects — such as a white dwarf binary pair — would create outwardly-expanding ripples in space-time that would ultimately “steal” kinetic energy from the objects themselves. These gravitational waves would be very subtle, yet in theory, observable.

Read: Astronomy Without a Telescope: Gravitational Waves

What researchers led by a team at The University of Texas at Austin have found is optical evidence of gravitational waves slowing down the stars in J0651. Originally observed in 2011 eclipsing each other (as seen from Earth) once every six minutes, the stars now eclipse six seconds sooner. This equates to a predicted orbital period reduction of about 0.25 milliseconds each year.*

“These compact stars are orbiting each other so closely that we have been able to observe the usually negligible influence of gravitational waves using a relatively simple camera on a 75-year-old telescope in just 13 months,” said study lead author J.J. Hermes, a graduate student at The University of Texas at Austin.

Based on these measurements, by April 2013 the stars will be eclipsing each other 20 seconds sooner than first observed. Eventually they will merge together entirely.

Although this isn’t “direct” observation of gravitational waves, it is evidence inferred by their predicted effects… akin to watching a floating lantern in a dark pond at night moving up and down and deducing that there are waves present.

“It’s exciting to confirm predictions Einstein made nearly a century ago by watching two stars bobbing in the wake caused by their sheer mass,” said Hermes.

As of early last year NASA and ESA had a proposed mission called LISA (Laser Interferometer Space Antenna) that would have put a series of 3 detectors into space 5 million km apart, connected by lasers. This arrangement of precision-positioned spacecraft could have detected any passing gravitational waves in the local space-time neighborhood, making direct observation possible. Sadly this mission was canceled due to FY2012 budget cuts for NASA, but ESA is moving ahead with developments for its own gravitational wave mission, called eLISA/NGO — the first “pathfinder” portion of which is slated to launch in 2014.

The study was submitted to Astrophysical Journal Letters on August 24. Read more on the McDonald Observatory news release here.

Inset image: simulation of binary black holes causing gravitational waves – C. Reisswig, L. Rezzolla (AEI); Scientific visualization – M. Koppitz (AEI & Zuse Institute Berlin)

*The difference in the eclipse time is noted as six seconds even though the orbital period decay of the two stars is only .25 milliseconds/year because of a pile-up effect of all the eclipses observed since April 2011. The measurements made by the research team takes into consideration the phase change in the J0651 system, which experiences a piling effect — similar to an out-of-sync watch — that increases relative to time^2 and is therefore a larger and easier number to detect and work with. Once that was measured, the actual orbital period decay could be figured out.