[/caption]
In an article earlier this month, I discussed the potential for discovering moons orbiting extrasolar planets. I’d used an image of an exoplant system with rings, prompting one reader to ask if those would be possible to detect. Apparently he wasn’t the only person wondering. A new paper looks more at exomoons and explores exoring systems.
The idea of detecting rings around distant planets dates back to at least 2004. Then, Barnes & Fortney suggested that rings would be potentially detectable from the eclipse they would cause if the photometric precision were as one part in ten-thousand. This is a big challenge, but one that’s more than met by telescopes like Kepler today. But for this to be possible, the rings needed to block the most light possible, meaning that they would have to be viewed face on, instead of edge on.
Fortunately, a study this year by Schlichting & Chang demonstrated that, even if the planet’s spin is aligned with the plane of orbit, it’s quite possible that the rings will be significantly warped due to gravitational interactions with the star.
So it should be possible, but what do astronomers need to look for?
The new paper attempts to answer this question by simulating light curves for a hypothetical ringed exoplanet. The first result is that the extra area of the star’s surface covered by the rings reduces the light detected. However, this is difficult to disentangle from the effects of simply having a larger planet that blocks the light.
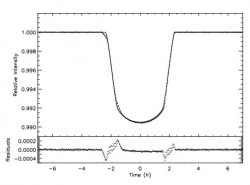
A second effect is based on the shape of the light curve (a graph of the brightness as a function of time) as the planet begins and ends the transit. In short, the semi-transparent nature of the rings makes the drop in brightness softer, rounding off the edges of the light curve. When modeled against a planet that lacked rings, this would be readily detectable for an instrument like Kepler.
With such precision, the team suggests that Kepler should be more than capable of detecting a ring system similar in size and nature to those of Saturn. However, other transit finding telescopes, such as CoRoT, would mistake the rings for a slightly larger planet.
In the future, the team plans to take their model and reexamine data from Kepler and CoRoT to search for both rings and moons.


Since we usually see exoplanets which cross in front of their stars, it is likely that the rings will be in the same plane and therefore unlikely to be spotted. I think the closest we will get is some vague “possibilities”.
Why is it likely? It doesn’t make sense to me.
If anything we WILL solve it.
– The paper discuss (at least) close giants, where the rings would be rocky (denser, thicker) but also warped by gravity quadrupole effects. The author’s are excited:
“Most interestingly, we find that many of the rings could have nontrivial Laplacian planes due to the increased effects of the orbital quadrupole caused by the exoplanets’ proximity to their host star, allowing a constraint on the J2 of extrasolar planets from ring observations. This is particular exciting, since a planet’s J2 reveals information about its interior structure. Furthermore, measurements of an exoplanet’s oblateness and of its J2, from warped rings, would together place limits on its spin period.”
– We see Saturn’s “paper-thin” (to scale) rings because the planet has a ~ 5 degree inclination.
Most planets are not oriented with their angular momentum axis perpendicular to the orbital plane. The Earth for instance is oriented 23-deg with respect to its orbital plane. So a ring similarly oriented will block light. For the angle ? between the angular momentum axis and the plane of the orbit any ring perpendicular to the angular momentum axis will present a blocking area that varies as cos?. In the limit the ring is on the plane of the orbit that blocking area is zero. There is then the question of how much light this blocking area attenuates. This will also vary as cos?, where light will have to pass through approximately a cos? varying amount of material in the ring, reaching a maximum at ? = ?/2, and a minimum at ? = 0. This works approximately for angles away from these limits So the amount of light blocked is the ratio of the two which is just a unit — cos?/cos? = 1. Now there is a funny problem when the cosines are zero. I think the physical situation goes to zero, but that will require more work.
Physically we can see that while the area of the ring decreases, light passing through it has to pass through more attenuating material. As a result a ring that is maybe 10 degrees from edge on can attenuate about as much light as a ring that is directed face on towards the observe, or a spacecraft telescope like Kepler. So this technique should be able to detect these rings.
LC
Iv always wondered, if we keep throwing enough junk up there round our planet, would it all coalesce one day as a ring of rubbish round our planet….?