Thanks to Space.com and the Tech Media Network for sharing this infographic showing how NASA’s OSIRIS-REx mission will reach out and grab a sample from asteroid RQ26 in 2020. Source SPACE.com:
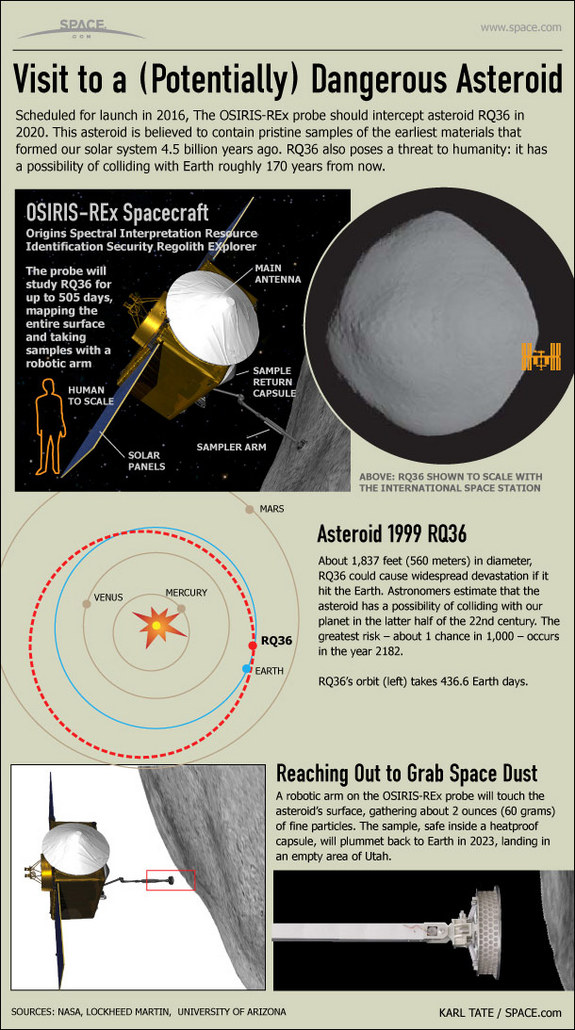
Source SPACE.com.
Thanks to Space.com and the Tech Media Network for sharing this infographic showing how NASA’s OSIRIS-REx mission will reach out and grab a sample from asteroid RQ26 in 2020. Source SPACE.com:

Source SPACE.com.
Comments are closed.
What is the advantage of the puff-and-sniff method over landing and scooping? Both seem to require low speeds. Hayabusa attempted the former but ended up doing something more like the latter, by accident.
This robot arm looks like it could be used as a pogo stick to launch the craft back to orbit. I suppose its purpose is to match the velocity of the asteroid without touching it, to avoid requiring such precision from the rockets. But wouldn’t it be easier just to use it as an anchor?
This is so similar to the Japanese mission. It would be cool if it pogoed down into a crater, found some specific interesting rocks from deep down, then pogoed back up and jumped back to orbit.
In the University of Arizona’s OSIRIS-REx pamphlet summary, they press the return of pristine regolith. Presumably they don’t want to dirty it with rocket exhaust if possible. (So maybe establish a slow drift before tagging the target.)
They also claim both NEAR and Hayabusa proximity operations know how, so it should have been influencing the chosen method.
You mentioned in the other article commentary that they seem to be trying hard to sample only the surface, which is the least pristine part.
What do you make of that?
Anyway… I’m not a spacecraft pilot, but NEAR and Hayabusa seem to have proven that crash-landing is acceptable. Rocket exhaust is unnecessary; just make that arm a literal, springy pogo stick.
Yeah, I wondered about that discrepancy myself. Didn’t I also say that perhaps the surface sample is more valuable, as they try to understand asteroid history? If not, that is a speculation I add now.
An interview with the principal investigator adds info:
“The next [principal instrument (my note)] is a visual near-infrared mapping spectrometer. It’s kind of like the cameras, but it’s basically designed to tell us about the mineralogy, and that includes organic material. It would be one of two instruments that help us understand where there’s variation at the surface. If the surface is patchy, we will go to an area where there’s a patch that’s rich in organics. …
The most technically challenging part will be dropping down to collect the sample. We’ll have to approach very slowly. It’s kind of like the duration of a kiss at my age. You approach the lady for a second or so, but you hang on for another four or five.
So you touch the surface, fire some very dry nitrogen gas to agitate the surface and collect the surface material in what looks like an old-fashioned car air filter.
And the arm that the sampling head is attached to is a little like a pogo stick: It can compress down to a stopping point and bounce back again, pushing away from the surface and then firing thrusters to pull away safely.
Most material is collected in the first second, but it takes another four seconds [for the sampling head (interview note)] to start to bounce back and push away from the surface.
Before collecting the sample, we’re going to practice the entire process of going to the surface, to make sure we get it right.
It’s very hard to land on a body with essentially no gravity, but it’s quite easy to sneak up on it and kiss it.”
So they are very deliberately going for the surface material. They also seem to claim the pogo stick is an easier method compared to earlier suggested methods (gravity landing, and IIRC anchor landing).
Perfect for a Space Station, with a complimentary earth mars transit orbit. Wonder how the orbital resonances work out. If its a differentiated body then it may well have useful minerals. This is going to be a cool mission. But I wish it was a geologist going to live on it for a year with some deep drilling gear and a lab instead of a little drone spacecraft.
Wikipedia (http://en.wikipedia.org/wiki/%28101955%29_1999_RQ36 ) gives an aphelion of 1.356 AU. Mars has a perihelion of 1.381, but an aphelion of 1.665.
I think we’d be better off trying to continually steer it back and forth than to hope for a natural resonance. (Frequent proximity to Earth or Mars would be destabilizing, I would think.) The Yarkovsky effect might be a good control mechanism.
Polished rocks have a higher albedo. Send a nuclear rock tumbler. Have some rovers expose and hide the shiny rocks to alter its rotation and velocity as desired.
Assuming it is a sphere with r = 280 m, the surface area is about 1 km^2. We should only have to “pave” half that if its rotation can be tuned. To finish in 10 years, we would want to cover 137 m^2 per day, which for reference is the floorspace of a modest American 3-bedroom house.
Well, the idea is to modify the Yarkovsky effect enough to steer it, not to pave the whole thing. Whether polishing it all to mirror finish is insufficient, or we’d only need 10%, I don’t know.
The time and energy required to polish/blast/knap/rework the rocks depends on their internal structure, which this probe apparently won’t elucidate, because it won’t collect any big ones :v( .
I think this would be a job for a robot, not an astronaut chain gang ;v) .
Interesting.
There may not be a really favorable resonance for earth to mars transits, however you could use the orbital momentum of the asteroid to slingshot spacecraft between the two planets. There may be some advantage to this if you wanted to set up a colony on mars and transport lots of materials from earth.
A tether slingshot system is also a means of steering by changing the asteroids center of mass. Additional induced spin by using the Yarkovsky – Yorp effect can also transfer that extra energy to a spacecraft. Mirrors lined on the equator of the body would create a kind of windmill effect. Although if its a rubble pile (likely) then too much spin will break it up.
Which could also be useful. 🙂
Incidentally you could also try the opposite and make the asteroid as dark as possible and use small mirrors spaced out over the body. But this effect is slow.
I still think that if you needed to push it quickly Mass drivers will be the way to go. (Ion Engine using pulverized regolith as reaction mass.) Which if done right could also burrow through the asteroid harvesting useful minerals and scientific data. How cool would it be to slice a hole right through it like a core sample. ?
Steering the rock would be a great project to undertake. Eliminate the threat to earth but at the same time develop a technological, economic and scientific paradigm.
Ion engines are optimized for small fuel reserves. For a rubble pile, you might as well fling rocks just a few times escape velocity (less than 1 cm/sec here, so 1 km/hr would do). This maximizes the momentum change per unit energy.
?|p| = m * (v_fling – v_escape)
E = m * (v_fling)^2 / 2
?|p| / E = 2 * (v_fling – v_escape) / (v_fling)^2
= 2 * (1/v_fling – v_escape / v_fling^2)
(d/dv_fling) ?|p|/E = 0
–v_fling^–2 = v_escape * –2 * v_fling^–3
v_fling = v_escape * 2
Ah, exactly twice the escape velocity is optimal.
I’m not sure if this would be more efficient than polishing the rocks. Over a sufficiently long timespan, I’m pretty sure polishing pays off :v) .
My physics sense tells me that the velocity of cast off is the escape velocity.
This minimization might work better with a ratio of the total energy change of the asteroid system plus ejected material to the energy of the ejected material. The rocket equation is of some help. The rocket equation is a conservation of momentum result with
d(mv)/dt = 0 — > (m – ?m)(v + ?v) – ?mV = 0
where V is the reaction mass velocity, ?v and ?m is the change in velocity and mass loss of the “rocket,” or in this case the asteroid, and m and v are the initial mass and velocity of the object. We set v = 0 and get
?v = V(?m/m)
and the velocity integrated up is v = V ln(m_i/m_f), for m_i the initial mass and m_f the final mass. If the change in mass is small we have
v ~= V(m_i/m_f – 1)
and the momentum of the asteroid at the end is p ~= V(m_i – m_f). We now let V = u – v_e, for v_e the escape velocity and u the velocity of the object cast off. This means V is the velocity of the cast off object “at infinity.”
Now suppose we want to minimize the kinetic energy of the asteroid K = (1/2)p^2/m_f for a given casting off kinetic energy E = (1/2)?mu^2. We construct a dimensionless ratio,
R = p^2/m_f /(?mu^2/= (p/u)^2/(?mm_f) = (?m/m_f) (1 – v_e/u)^2.
BTW, it is important to work with a dimensionless ratio. So we minimize this for a given ?m and compute the u. So we minimize
F(u) = (1 – v_e/u)^2, — > dF(u)/du = -2(1 – v_e/u)*v_e/u^2,
and this is zero at v_e = u. This seems a little strange given the rocket equation formula, but I will discuss that below.
We then take the second derivative to determine whether this is a max or min and we get
d^2F(u)/du^2 = 4(1 – v_e/u)*(v_e/u^2)^2 – 2(v_e/u^2)^2
which at u = v_e is -2 < 0 and so it is a min, what we want. It is also clear that u = v_e is the minimum kinetic energy we can impart on the mass.
It sounds odd that we have v ~= V(m_i/m_f – 1), which for V = u – v_e is zero at u = v_e. However, for u = v_e the asteroid is moving out until the cast off object reaches infinity. The purpose of doing this is to create a displacement of the asteroid, and as the cast off object reaches “infinity” the asteroid will reach some displacement distance away.
LC
We’re describing completely different things. If the applied velocity is exactly equal to escape velocity, then clearly there is no change in asteroid momentum as the reaction mass never left at all.
Displacement of the center of mass is also zero. If you push enough rocks away at escape velocity in the same direction, they will coalesce to another asteroid in the same place that you started. (The first part is a consequence of conservation of momentum for any system, but the second part is the unusual result of the objects slowing down enough to recombine.)
The distance to the reaction mass will only reach infinity as time approaches infinity.
I should read up on the rocket equation, but you lost me at “d(mv)/dt = 0 … m and v are the initial mass and velocity of the object.” That’s taking the derivative of the product of two constants (where one constant is zero).
If you kept firing away little mass elements ?m at any velocity the center of mass will remain. If you do this at the escape velocity then as t — > ? you will end up with the two sets of masses arbitrarily far away from the center of mass. I just wrote this up because if you are interested in minimizing energy use in the nudging of an asteroid you don’t need to have v = 2v_esc, which has 4 times the energy as v = v_esc.
LC
Depending on how it needs to be nudged, the energy can be anything — v_esc may too be excessive.
If I toss a rock in proximity to a larger body, and it only escapes the local sphere of influence, then it has effectively escaped.
Maybe you could even toss the rock up, modify the particular gravity field you pass through, then catch it again and regain more energy than you spent?
Anyway, as I noted… my sense is that the kind of delta-v required for repeated round trips requires much higher velocities than v_esc, since a fairly small amount of constant power will tear the asteroid apart in a matter of days or years.
If the intention is to nudge the asteroid with the smallest amount of energy, then it makes not much difference.
LC
Many-body systems being chaotic, the smallest nudge eventually makes the same difference as any…
In the “faster down than up” vein, I wonder if tidal force could be harvested to power the asteroid on to the next encounter, while also making closer flybys possible.
Also there seems to be a force acting on the column width here!
Help I’m trapped in this tiny little box!
I write in a larger column above. LC
If the intention is to nudge the asteroid with the smallest amount of energy, then it makes not much difference.
LC
Gravity is a weak force, and for a small object like an asteroid the gravitational potential is very small. Also as a conservative force it is hard to extract energy from the gravity field. The most obvious way is through heat involved with a collision, or for large tidal forces there can be heating of infalling material.
LC
You lost me in:
a) trying to minimize R = asteroid energy for energy of thrown mass (i.e. efficiency) instead of maximizing it,
b) having a negative 2nd derivative, which indicates a local maximum, as indicating a minimum.
Maybe these two points can be reconciled?
Sorry, that was a “brain fart.” I made a – sign error, but it is now fixed. That is what happens when you write these too quickly.
LC
Sorry, that was a “brain fart.” I made a – sign error, but it is now fixed. That is what happens when you write these too quickly.
LC
I would like to donate my snowblower for the job. It could probably fling rocks too.
I feel sorry for the people who will be alive when that time comes. They’ll probably be freaking out. Although, by then they’ll probably be able to avoid such objects with some super space asteroid deflection technology, lol.
why not drill a core and return that, much more useful data i would think?
i vaccum the dust off my carpet but that doesn’t really tell me much about what the carpet is made of!
This probe uses a “puff” of Nitrogen gas to lift particulates off the surface of the asteroid and into a collection container. I am assuming the gas will not freeze into a liquid or ice particles? Would that matter other than in species differentiation or sorting? We HAVE found temperatures on the moon where liquid N2 could exist….