It now seems clear that dark matter interacts more than just gravitationally. Earlier studies have hinted at this, and a new study supports the idea even further. What’s interesting about this latest work is that it studies dark matter interactions through entropy.
Entropy is a subtle and powerful concept in physics. It was first introduced as a property in thermodynamics, but it plays a role in everything from black holes to the flow of time. It’s also rather difficult to define without relying on mathematics.

Entropy is often described as a measure of the disorder of a system. Ice, for example, with its water molecules arranged into symmetrical crystals has lower entropy than water, with its chaotic dance of water molecules. Since warmer things tend to be more disordered, entropy is also related to the temperature of an object. Hence, the second law of thermodynamics states that the entropy of a system can’t decrease, which also means that heat flows from warm objects to cold ones.
For this latest work, entropy is better described in terms of how likely an object is to be in a particular state. Imagine lighting a scented candle in the corner of a room. While it is statistically for the scent of the candle to hover around the candle, the motion of the air in the room will most likely spread the scent throughout the room. An evenly spread scent is the most likely outcome because it is the state with the maximum entropy. It’s a state also known as thermodynamic equilibrium.

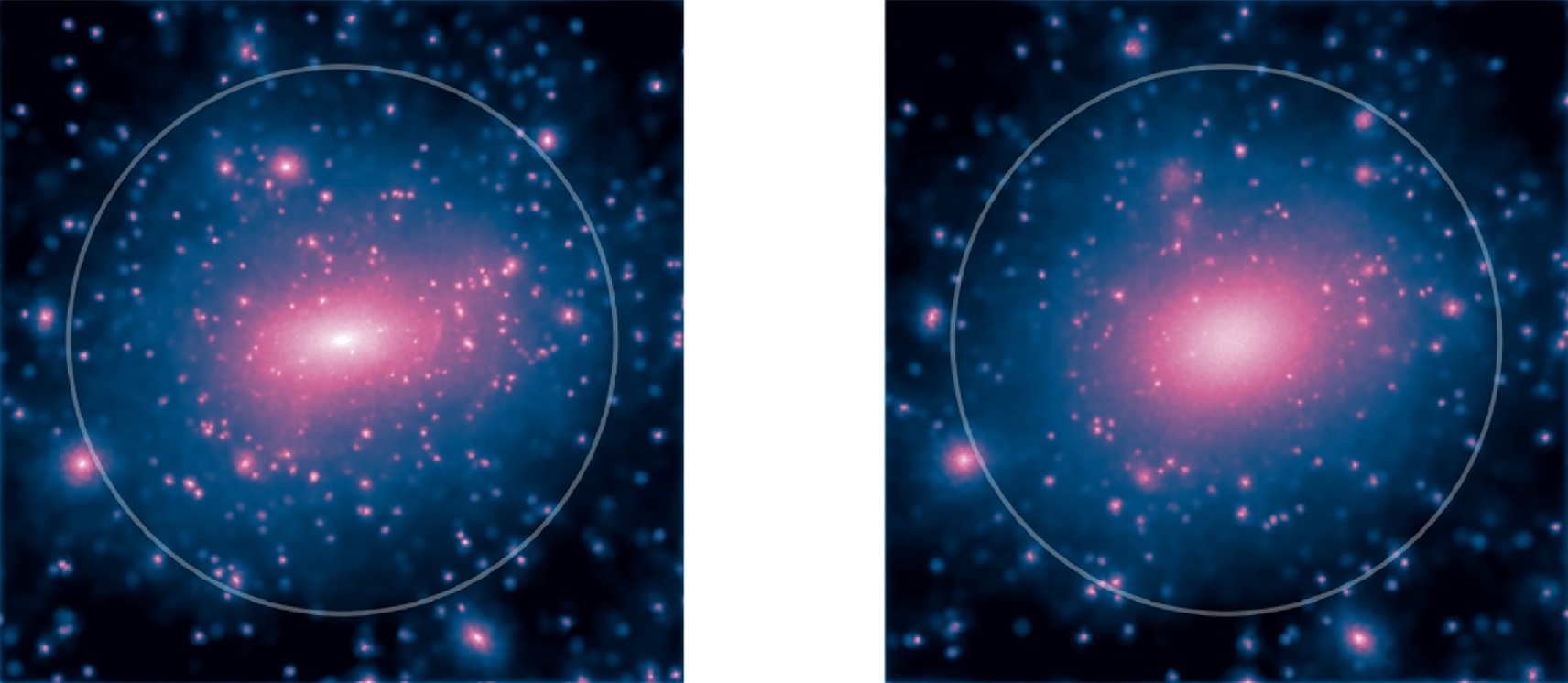
In this new study, the team used computer models to calculate the state of maximum entropy for dark matter in dwarf galaxies. The distribution of dark matter determines how strongly light will gravitationally lens. When the team looked at theoretical lensing by galactic dark matter in maximum entropy, they found it agreed with observed lensing around dwarf galaxies. Thus, dark matter seems to be in a state of maximum entropy.
This means dark matter must interact in some way. The scent in a room reaches maximum entropy because the aroma molecules interact strongly with molecules of air. All those interactions work to increase the entropy of the room. Dark matter doesn’t interact strongly with regular matter, so this study suggests it strongly interacts with itself.
Without knowing exactly what dark matter is, we don’t know how it can interact. But this study and others further confirm the reality of dark matter.
Reference: Brinckmann, Thejs, et al. “The structure and assembly history of cluster-sized haloes in self-interacting dark matter.” Monthly Notices of the Royal Astronomical Society 474.1 (2018): 746-759.
Reference: Almeida, Jorge Sánchez, Ignacio Trujillo, and Angel Ricardo Plastino. “The principle of maximum entropy explains the cores observed in the mass distribution of dwarf galaxies.” Astronomy & Astrophysics 642 (2020): L14.

This Self-interacting dark matter model [“Self-interacting dark matter” @ Wikipedia] is literary a shot in the dark, of course.
The current Cold Dark Matter model explains the observations better than other dark matter models, and the cusp-core problem the paper alludes to was solved 2015 by including galaxy gas outflows [ https://astrobites.org/2015/06/12/the-labor-of-outflows-against-dark-matter-halo/ ].
“Alternative dark matter models such as warm dark matter (WDM) and self-interating dark matter (SIDM) are introduced to resolve the cusp-core problem. However, ?CDM cosmology may still give rise to cored halos, by utilizing astrophysical processes that “push against” dark matter halos such that they are no longer steep and cuspy in the centers. One such process is outflow from star forming activities such as supernovae. … the [CDM] DC14 model closely tracks observations … both WDM and SIDM are not able to fit the velocity function and Tully-Fisher relation as well as we expect.”
I don’t see that the paper tries to test their cored model against the velocity function and Tully-Fisher relation.
Also, maximum entropy is an information theoretic concept, not a physically motivated result [“Principle of maximum entropy” @ Wikipedia].
Dark matter is smoothly distributed throughout the Universe and is displaced by visible matter. The smoothly distributed dark matter is a supersolid that is displaced by ordinary matter. The supersolid dark matter displaced by the quarks the Earth consist of, pushing back and exerting pressure toward the Earth, causes gravity. The supersolid dark matter displaced by the quarks a galaxy consists of, pushing back and exerting pressure toward the galaxy, causes the stars to orbit the galactic center at the rate in which they do.
No, dark matter isn’t displaced, for example the Milky Way has both a dark matter and baryonic matter halo, and it isn’t a supersolid condensate either – see the illustration to the article!