Space and astronomy news
The tension between quantum mechanics and relativity has long been a central split in modern-day physics. Developing a theory of quantum gravity remains one of the great outstanding challenges of the discipline. And yet, no one has yet been able to do it. But as we collect more data, it shines more light on the potential solution, even if some of that data happens to show negative results.
Continue reading “Scientists Test for Quantum Gravity”
Hawking radiation is one of the most famous physical processes in astronomy. Through Hawking radiation, the mass, and energy of a black hole escape over time. It’s a brilliant theory, and it means that black holes have a finite lifetime. If Hawking radiation is true. Because as famous as it is, Hawking radiation is unproven. The theory is not even theoretically proven.
Continue reading “If Black Holes Evaporate, Everything Evaporates”
In the classical theory of general relativity, black holes are relatively simple objects. They can be described by just three properties: mass, charge, and rotation. But we know that general relativity is an incomplete theory. Quantum mechanics is most apparent in the behavior of tiny objects, but it also plays a role in large objects such as black holes. To describe black holes at a quantum level, we need a theory of quantum gravity. We don’t have a complete theory yet, but what know so far is that quantum mechanics makes black holes more complex, giving them properties such as temperature and perhaps even pressure.
Continue reading “We Knew Black Holes Have a Temperature. It Turns out They Also Have a Pressure”
In my last post, I talked about the idea of warp drive and whether it might one day be possible. Today I’ll talk about another faster-than-light trick: wormholes.
Continue reading “Wormholes Could Allow Travel Across the Universe, as Long as Your Spacecraft is Microscopic”
In physics, there are two main ways to model the universe. The first is the classical way. Classical models such as Newton’s laws of motion and Einstein’s theory of relativity assume that the properties of an object such as its position and motion are absolute. There are practical limits to how accurately we can measure an object’s path through space and time, but that’s on us. Nature knows their motion with infinite precision. Quantum models such as atomic physics assume that objects are governed by interactions. These interactions are probabilistic and indefinite. Even if we constrain an interaction to limited outcomes, we can never know the motion of an object with infinite precision, because nature doesn’t allow it.
Continue reading “A new Approach Could Tease out the Connection Between Gravity and Quantum Mechanics”
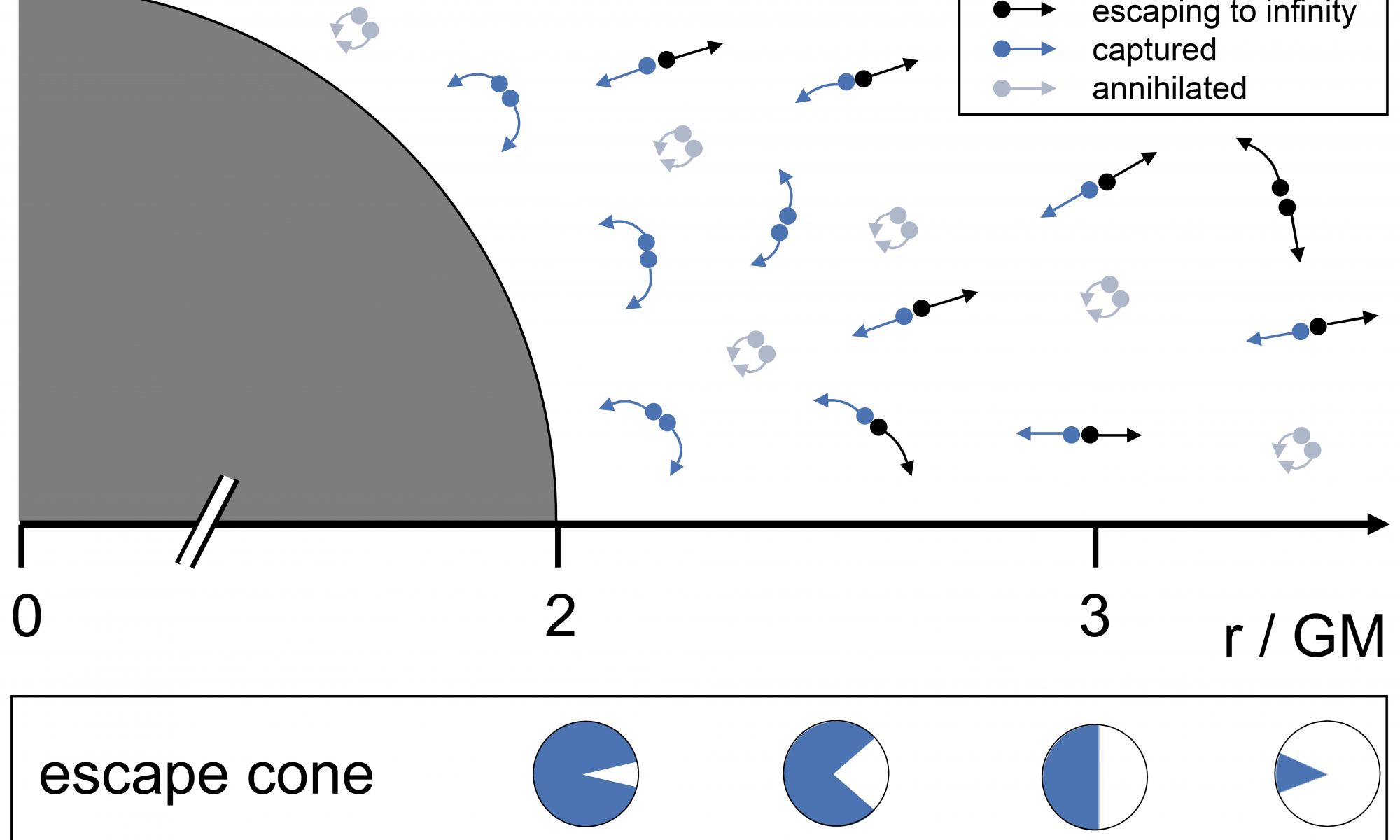
Most of the matter of the universe is of a form unknown to physics. While we don’t know what the identity of the dark matter is, a new insight provided by quantum gravity is helping to drastically narrow down its mass.
Continue reading “Narrowing Down the Mass of Dark Matter”
[/caption]
General relativity, Einstein’s theory of gravity, gives us a useful basis for mathematically modeling the large scale universe – while quantum theory gives us a useful basis for modeling sub-atomic particle physics and the likely small-scale, high-energy-density physics of the early universe – nanoseconds after the Big Bang – which general relativity just models as a singularity and has nothing else to say on the matter.
Quantum gravity theories may have more to say. By extending general relativity into a quantized structure for space-time, maybe we can bridge the gap between small and large scale physics. For example, there’s doubly special relativity.
With conventional special relativity, two different inertial frames of reference may measure the speed of the same object differently. So, if you are on a train and throw a tennis ball forward, you might measure it moving at 10 kilometers an hour. But someone else standing on the train station platform watching your train pass by at 60 kilometers an hour, measures the speed of the ball at 60 + 10 – i.e. 70 kilometers an hour. Give or take a few nanometers per second, you are both correct.
However, as Einstein pointed out, do the same experiment where you shine a torch beam, rather than throw a ball, forward on the train – both you on the train and the person on the platform measure the torch beam’s speed as the speed of light – without that additional 60 kilometers an hour – and you are both correct.
It works out that for the person on the platform, the components of speed (distance and time) are changed on the train so that distances are contracted and time dilated (i.e. slower clocks). And by the math of Lorenz transformations, these effects become more obvious the faster than train goes. It also turns out that the mass of objects on the train increase as well – although, before anyone asks, the train can’t turn into a black hole even at 99.9999(etc) per cent of the speed of light.
Now, doubly special relativity, proposes that not only is the speed of light always the same regardless of your frame of reference, but Planck units of mass and energy are also always the same. This means that relativistic effects (like mass appearing to increase on the train) do not occur at the Planck (i.e. very small) scale – although at larger scales, doubly special relativity should deliver results indistinguishable from conventional special relativity.
Doubly special relativity might also be generalized towards a theory of quantum gravity – which, when extended up from the Planck scale, should deliver results indistinguishable from general relativity.
It turns out that at the Planck scale e = m, even though at macro scales e=mc2. And at the Planck scale, a Planck mass is 2.17645 × 10-8 kg – supposedly the mass of a flea’s egg – and has a Schwarzschild radius of a Planck length – meaning that if you compressed this mass into such a tiny volume, it would become a very small black hole containing one Planck unit of energy.
To put it another way, at the Planck scale, gravity becomes a significant force in quantum physics. Although really, all we are saying that is that there is one Planck unit of gravitational force between two Planck masses when separated by a Planck length – and by the way, a Planck length is the distance that light moves within one unit of Planck time!
And since one Planck unit of energy (1.22×1019 GeV) is considered the maximal energy of particles – it’s tempting to consider that this represents conditions expected in the Planck epoch, being the very first stage of the Big Bang.
It all sounds terribly exciting, but this line of thinking has been criticized as being just a trick to make the math work better, by removing important information about the physical systems under consideration. You also risk undermining fundamental principles of conventional relativity since, as the paper below outlines, a Planck length can be considered an invariable constant independent of an observer’s frame of reference while the speed of light does become variable at very high energy densities.
Nonetheless, since even the Large Hadron Collider is not expected to deliver direct evidence about what may or may not happen at the Planck scale – for now, making the math work better does seem to be the best way forward.
Further reading: Zhang et al. Photon Gas Thermodynamics in Doubly Special Relativity.