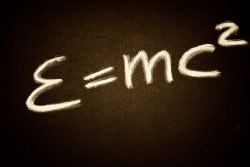Isaac Newton Archives

November 10, 2015November 30, 2016 by Matt Williams

Who Was Sir Isaac Newton?

The 17th century was an auspicious time for the sciences, with groundbreaking discoveries being made in astronomy, physics, mechanics, optics, and the natural sciences. At the center of all this was Sir Isaac Newton, the man who is widely recognized as being one of the most influential scientists of all time and as a key figure in the Scientific Revolution.

An English physicist and mathematician, Newton made several seminal contributions to the field of optics, and shares credit with Gottfried Leibniz for the development of calculus. But it was Newton’s publication of Philosophiæ Naturalis Principia Mathematica (“Mathematical Principles of Natural Philosophy”), for which he is most famous. Published in 1687, this treatise laid the foundations for classical mechanics, a tradition which would dominate scientists’ view of the physical universe for the next three centuries.

Early Life:

Isaac Newton was born on January 4th, 1643, – or December 25th, 1642 according to the Julian Calendar (which was in use in England at the time) – in Woolsthorpe-by-Colsterworth, a hamlet in the county of Lincolnshire. His father, for whom he was named, was a prosperous farmer who had died three months before his birth. Having been born prematurely, Newton was small as a child.

His mother, Hannah Ayscough, remarried when he was three to a Reverend, leaving Newton in the care of his maternal grandmother. His mother would go on to have three more children with her new husband, which became Newton’s only siblings. Because of this, Newton apparently had a rocky relationship with his stepfather and mother for some time.

William Blake's Newton (1795), depicted as a divine geometer. Credit: William Blake Archive/Wikipedia — *William Blake’s Newton (1795), depicted as a divine geometer. Credit: William Blake Archive/Wikipedia*

By the time Newton was 17, his mother was widowed again. Despite her hopes that Newton would become a farmer, like his father, Newton hated farming and sought to become an academic. His interests in engineering, mathematics and astronomy were evident from an early age, and Newton began his studies with an aptitude for learning and inventing that would last for the rest of his life.

Education:

Between the ages of 12 and 21, Newton was educated at The King’s School, Grantham, where he learned Latin. While there, he became the top-ranked student, and received recognition for his building of sundials and models of windmills. By 1661, he was admitted to Trinity College, Cambridge, where he paid his way by performing a valet’s duties (what was known as a subsizar).

During his first three years at Cambridge, Newton was taught the standard curriculum, which was based on Aristotelian theory. But Newton was fascinated with the more advanced science and spent all his spare time reading the works of modern philosophers and astronomers, such as René Descartes, Galileo Galilei, Thomas Street, and Johannes Kepler.

The result was a less-than-stellar performance, but his dual focus would also lead him to make some of his most profound scientific contributions. In 1664, Newton received a scholarship, which guaranteed him four more years until he would get his Masters of Arts degree.

David Loggan's print of 1690 showing Nevile's Great Court (foreground) and Nevile's Court with the then-new Wren Library (background) — New Court had yet to be built. Credit: Cantabrigia Illustrata/Cambridge (1690) — *David Loggan’s print of Trinity College, Cambridge, showing Nevile’s Great Court (foreground) and the then-new Wren Library (background). Credit: Cantabrigia Illustrata/Cambridge (1690)*

In 1665, shortly after Newton obtained his B.A., the university temporarily closed due to the outbreak of the Great Plague. Using this time to study at home, Newton developed a number of ideas he had which would eventually cement to become his theories on calculus, optics and the law of gravitation (see below).

In 1667, he returned to Cambridge and was elected as a fellow of Trinity, though his performance was still considered less than spectacular. However, in time, his fortunes improved and he gained recognition for his abilities. In 1669, he received his M.A. (before he had turned 27), and published a treatise expounding on his mathematical theories for dealing with infinite series.

By 1669, he succeeded his one-time teacher and mentor Isaac Barrow – a theologian and mathematician who discovered the fundamental theorem of calculus – and became the Lucasian Chair of Mathematics at Cambridge. In 1672, he was elected a Fellow of the Royal Society, which he would remain a part of until the end of his life.

Scientific Achievements:

While studying at Cambridge, Newton maintained a second set of notes which he entitled “Quaestiones Quaedam Philosophicae” (“Certain Philosophical Questions“). These notes, which were the sum total of Newton’s observations about mechanical philosophy, would lead him to discover the generalized binomial theorem in 1665, and allowed him to develop a mathematical theory that would lead to his development of modern calculus.

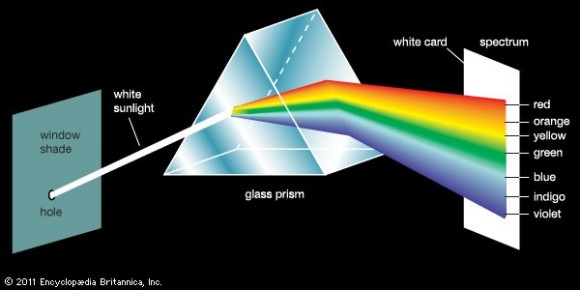
Newton's experiment using a prism revealed that light is refracted based on color. Credit: britannica.com — *Newton’s experiment using a prism revealed that light is refracted based on color. Credit: britannica.com*

However, Newton’s earliest contributions were in the form of optics, which he delivered during annual lectures while holding the position of Lucasian Chair of Mathematics. In 1666, he observed that light entering a prism as a circular ray exits in the form of an oblong, demonstrating that a prism refracts different colors of light at different angles. This led him to conclude that color is a property intrinsic to light, a point which had been debated in prior years.

In 1668, he designed and constructed a reflecting telescope, which helped him prove his theory. From 1670 to 1672, Newton continued to lecture on optics and investigated the refraction of light, demonstrating that the multicoloured spectrum produced by a prism could be recomposed into white light by a lens and a second prism.

He also demonstrated that colored light does not change its properties, regardless of whether it is reflected, scattered, or transmitted. Thus, he observed that color is the result of objects interacting with already-colored light, rather than objects generating the color themselves. This is known as Newton’s theory of color.

The Royal Society asked for a demonstration of his reflecting telescope in 1671, and the organization’s interest encouraged Newton to publish his theories on light, optics and color. This he did in 1672 in a small treatise entitled Of Colours, which would later be published in a larger volume containing his theories on the “corpuscular” nature of light.

Replica of Newton's second Reflecting telescope that he presented to the Royal Society in 1672. — *Replica of Newton’s second Reflecting telescope that he presented to the Royal Society in 1672. Credit: Wikipedia Commons*

In essence, Newton argued that light was composed of particles (or corpuscles), which he claimed were refracted by accelerating into a denser medium. In 1675, he published this theory in a treatise titled “Hypothesis of Light“, in which he also posited that ordinary matter was composed of larger corpuscles and about the existence of an ether that transmitted forces between particles.

After discussing his ideas with Henry More, an English theosophist and a member of the Cambridge Platonists, Newton’s interest in alchemy was revived. He then replaced his theory of an ether existing between particles in nature with occult forces, based on Hermetic ideas of attraction and repulsion between particles. This reflected Newton’s ongoing interest in both the alchemical and scientific, for which there was no clear distinction at the time.

In 1704, Newton published all of his theories on light, optics and colors into a single volume entitled Opticks: Or, A treatise of the Reflections, Refractions, Inflections and Colours of Light. In it, he speculated that light and matter could converted into one another through a kind of alchemical transmutation, and verged on theories of sound waves in order to explain repeated patterns of reflection and transmission.

While later physicists favored a purely wavelike explanation of light to account for the interference patterns and the general phenomenon of diffraction, their findings owed a great deal to Newton’ theories. Much the same is true of today’s quantum mechanics, photons, and the idea of wave–particle duality, which bear only a small resemblance to Newton’s understanding of light.

This set of papers documents some of Newton's early mathematical thinking, work that would develop into his theories of calculus. The texts include extracts he made from books he was reading and various notes and calculations - often on small scraps of paper he had to hand. Credit: newtonproject.sussex.ac.uk — *Excerpt from Newton’s “Quaestiones Quaedam Philosophicae”, a collection of observations that would lead to his development of modern calculus. Credit: newtonproject.sussex.ac.uk*

Though both he and Leibniz are credited with having developed calculus independently, both men became embroiled in a controversy over who discovered it first. Though Newton’s work in developing modern calculus began in the 1660s, he was reluctant to publish it, fearing controversy and criticism. As such, Newton didn’t publish anything until 1693 and did not give a full account of his work until 1704, whereas Leibniz began publishing a full account of his methods in 1684.

However, Newton earlier works in mechanics and astronomy involved extensive use of calculus in geometric form. This includes methods involving “one or more orders of the infinitesimally small” in his 1684 work, De motu corporum in gyrum (“On the motion of bodies in orbit”), and in Book I of the Principia, which he referred to as “the method of first and last ratios”.

Universal Gravitation:

In 1678, Newton suffered a complete nervous breakdown, most likely due to overwork and an ongoing feud with fellow Royal Society member Robert Hooke (see below). The death of his mother a year later caused him to become increasingly isolated, and for six years he withdrew from correspondence with other scientists, except where they initiated it.

During this hiatus, Newton renewed his interest in mechanics and astronomy. Ironically, it was thanks to a brief exchange of letters in 1679 and 1680 with Robert Hooke that would lead him to make his greatest scientific achievements. His reawakening was also due to the appearance of a comet in the winter of 1680–1681, about which he corresponded with John Flamsteed – England’s Astronomer Royal.

Thereafter, Newton began considering gravitation and its effect on the orbits of planets, specifically with reference to Kepler’s laws of planetary motion. After his exchanges with Hooke, he worked out proof that the elliptical form of planetary orbits would result from a centripetal force inversely proportional to the square of the radius vector.

Newton communicated his results to Edmond Halley (discoverer of “Haley’s Comet”) and to the Royal Society in his De motu corporum in gyrum. This tract, published in 1684, contained the seed that Newton would expand to form his magnum opus, the Principia. This treatise, which was published in July of 1687, contained Newton’s three laws of motion. These laws stated that:

When viewed in an inertial reference frame, an object either remains at rest or continues to move at a constant velocity, unless acted upon by an external force.
The vector sum of the external forces ( $F)$ on an object is equal to the mass ( $m)$ of that object multiplied by the acceleration vector ( $a)$ of the object. In mathematical form, this is expressed as: F=ma
When one body exerts a force on a second body, the second body simultaneously exerts a force equal in magnitude and opposite in direction on the first body.

Together, these laws described the relationship between any object, the forces acting upon it and the resulting motion, laying the foundation for classical mechanics. The laws also allowed Newton to calculate the mass of each planet, calculate the flattening of the Earth at the poles and the bulge at the equator, and how the gravitational pull of the Sun and Moon create the Earth’s tides.

In the same work, Newton presented a calculus-like method of geometrical analysis using ‘first and last ratios’, worked out the speed of sound in air (based on Boyle’s Law), accounted for the precession of the equinoxes (which he showed were a result of the Moon’s gravitational attraction to the Earth), initiated the gravitational study of the irregularities in the motion of the moon, provided a theory for the determination of the orbits of comets, and much more.

This volume would have a profound effect on the sciences, with its principles remaining canon for the following 200 years. It also informed the concept of universal gravitation, which became the mainstay of modern astronomy, and would not be revised until the 20th century – with the discovery of quantum mechanics and Einstein’s theory of General Relativity.

Newton and the “Apple Incident”:

The story of Newton coming up with his theory of universal gravitation as a result of an apple falling on his head has become a staple of popular culture. And while it has often been argued that the story is apocryphal and Newton did not devise his theory at any one moment, Newton himself told the story many times and claimed that the incident had inspired him.

In addition, the writing’s of William Stukeley – an English clergyman, antiquarian and fellow member of the Royal Society – have confirmed the story. But rather than the comical representation of the apple striking Netwon on the head, Stukeley described in his Memoirs of Sir Isaac Newton’s Life (1752) a conversation in which Newton described pondering the nature of gravity while watching an apple fall.

“…we went into the garden, & drank thea under the shade of some appletrees; only he, & my self. amidst other discourse, he told me, he was just in the same situation, as when formerly, the notion of gravitation came into his mind. “why should that apple always descend perpendicularly to the ground,” thought he to himself; occasion’d by the fall of an apple…”

John Conduitt, Newton’s assistant at the Royal Mint (who eventually married his niece), also described hearing the story in his own account of Newton’s life. According to Conduitt, the incident took place in 1666 when Newton was traveling to meet his mother in Lincolnshire. While meandering in the garden, he contemplated how gravity’s influence extended far beyond Earth, responsible for the falling of apple as well as the Moon’s orbit.

Sapling of the reputed original tree that inspired Sir Isaac Newton to consider gravitation. Credit: Wikipedia Commons/Loodog — *Sapling of the reputed original tree that inspired Sir Isaac Newton to consider gravitation, located on the grounds of Cambridge. Credit: Wikipedia Commons/Loodog*

Similarly, Voltaire wrote n his Essay on Epic Poetry (1727) that Newton had first thought of the system of gravitation while walking in his garden and watching an apple fall from a tree. This is consistent with Newton’s notes from the 1660s, which show that he was grappling with the idea of how terrestrial gravity extends, in an inverse-square proportion, to the Moon.

However, it would take him two more decades to fully develop his theories to the point that he was able to offer mathematical proofs, as demonstrated in the Principia. Once that was complete, he deduced that the same force that makes an object fall to the ground was responsible for other orbital motions. Hence, he named it “universal gravitation”.

Various trees are claimed to be “the” apple tree which Newton describes. The King’s School, Grantham, claims their school purchased the original tree, uprooted it, and transported it to the headmaster’s garden some years later. However, the National Trust, which holds the Woolsthorpe Manor (where Newton grew up) in trust, claims that the tree still resides in their garden. A descendant of the original tree can be seen growing outside the main gate of Trinity College, Cambridge, below the room Newton lived in when he studied there.

Feud with Robert Hooke:

With the Principia, Newton became internationally recognized and acquired a circle of admirers. It also led to a feud with Robert Hooke, with whom he had a troubled relationship in the past. With the publication of his theories on color and light in 1671/72, Hooke criticized Newton in a rather condescending way, claiming that light was composed of waves and not colors.

While other philosophers were critical of Newton’s idea, it was Hooke (a member of the Royal Society who had performed extensive work in optics) that stung Newton the worst. This led to the acrimonious relationship between the two men, and to Newton almost quitting the Royal Society. However, the intervention of his colleagues convinced him to stay on and the matter eventually died down.

However, with the publication of the Principia, matters once again came to a head, with Hooke accusing Newton of plagiarism. The reason for the charge had to do with the fact that earlier in 1684, Hooke had made comments to Edmond Halley and Christopher Wren (also members of the Royal Society) about ellipses and the laws of planetary motion. However, at the time he did not offer a mathematical proof.

Nevertheless, Hooke claimed that he had discovered the theory of inverse squares and that Newton had stolen his work. Other members of the Royal Society believed the charge to be unfounded, and demanded that Hooke release the mathematical proofs to substantiate this claim. In the meantime, Newton removed all reference to Hooke in his notes and threatened to withdraw the Principia from subsequent publishing altogether.

Edmund Halley, who was a friend to both Newton and Hooke, tried to make peace between the two. In time, he was able to convince Newton to insert a joint acknowledgement of Hooke’s work in his discussion of the law of inverse squares. However, this did not placate Hooke, who maintained his charge of plagiarism.

Newton's own copy of his Principia, with hand-written corrections for the second edition. Credit: Trinity Cambridge/Andrew Dunn — *Newton’s own copy of his Principia, with hand-written corrections for the second edition. Credit: Trinity Cambridge/Andrew Dunn*

As time moved on, Newton’s fame continued to grow while Hooke’s continued to diminish. This caused Hooke to become increasingly embittered and more protective of what he saw as his work, and he spared no opportunity to lash out at his rival. The feud finally ended in 1703, when Hooke died and Newton succeeded him as president of the Royal Society.

Other Accomplishments:

In addition to his work in astronomy, optics, mechanics, physics and alchemy, Newton also had a keen interest in religion and the Bible. During the 1690’s, he wrote several religious tracts that addressed literal and symbolic interpretations of the Bible. For instance, his tract on the Holy Trinity – sent to the famous political philosopher and social theorist John Locke and unpublished until 1785 – questioned the veracity of 1 John 5:7, the description which the Holy Trinity is based on.

Later religious works – like The Chronology of Ancient Kingdoms Amended (1728) and Observations Upon the Prophecies of Daniel and the Apocalypse of St. John (1733) – also remained unpublished until after his death. In Kingdoms, he dealt with the chronology of various ancient kingdoms – the First Ages of the Greeks, ancient Egyptians, Babylonians, Medeans and Persians – and offered a description of the Temple of Solomon.

In Prophecies, he addressed the Apocalypse, as foretold within the Book of Daniel and Revelations, and espoused his belief that it would take place in 2060 CE (though other possible dates included 2034 CE). In his textual criticism titled An Historical Account of Two Notable Corruptions of Scripture (1754), he placed the crucifixion of Jesus Christ on April 3rd, AD 33, which agrees with a traditionally accepted date.

*Portrait of Newton in 1702, painted by Godfrey Kneller. Credit: National Portrait Gallery, London*

In 1696, he moved to London to take up the post of warden of the Royal Mint, where he took charge of England’s great recoining. Newton would remain in this post for 30 years, and was perhaps the best-known Master of the Mint. So serious was his commitment to the role that he retired from Cambridge in 1701 to oversee the reform of England’s currency and the punishment of counterfeiters.

As Warden, and afterwards Master, of the Royal Mint, Newton estimated that 20 percent of the coins taken in during the Great Recoinage of 1696 were counterfeit. Conducting many investigations personally, Newton traveled to taverns and bars in disguise to gather evidence, and conducted more than 100 cross-examinations of witnesses, informers, and suspects – which led to the successful prosecution of 28 counterfeit coiners.

Newton was a member of the Parliament of England for Cambridge University in 1689–90 and 1701–2. In addition to being President of the Royal Society in 1703, he was an associate of the French Académie des Sciences. In April 1705, Queen Anne knighted Newton during a royal visit to Trinity College, Cambridge, making him the second scientist to be knighted (after Sir Francis Bacon).

Death and Legacy:

Towards the end of his life, Newton took up residence at Cranbury Park near Winchester with his niece and her husband, where he would stay until his death. By this time, Newton had become one of the most famous men in Europe and his scientific discoveries were unchallenged. He also had become wealthy, investing his sizable income wisely and bestowing sizable gifts to charity.

Newton's tomb in Westminster Abbey. Credit: Wikipedia Commons/Klaus-Dieter Keller — *Newton’s tomb in Westminster Abbey. Credit: Wikipedia Commons/Klaus-Dieter Keller*

At the same time, Newton’s physical and mental health began to decline. By the time he reached 80 years of age, he began experiencing digestive problems and had to drastically change his diet and lifestyle. His family and friends also began to worry about his mental stability, as his behavior became increasingly erratic.

Then, in 1727, Newton experienced severe pain in his abdomen and lost consciousness. He died in his sleep on the next day, on March 2oth, 1727 (Julian Calendar; or March 31st, 1727, Gregorian Calendar) at the age of 84. He was buried in tomb at Westminster Abbey. And as a bachelor, he had divested much of his estate to relatives and charities during his final years.

After his death, Newton’s hair was examined and found to contain mercury, probably resulting from his alchemical pursuits. Mercury poisoning has been cited as a reason for Newton’s eccentricity in later life, as well as the nervous breakdown he experienced in 1693. Isaac Newton’s fame grew even more after his death, as many of his contemporaries proclaimed him to be the greatest genius who ever lived.

These claims were not without merit, as his laws of motion and theory of universal gravitation were unparalleled in his the time. In addition to being able to bring the orbits of the planets, the Moon, and even comets into one coherent and predictable system, he also invented modern calculus, revolutionized our understanding of light and optics, and established scientific principles that would remain in use for the following 200 years.

Einstein Lecturing — *Albert Einstein was one of Newton’s many admirers, claiming that to Newton, nature was “an open book, whose letters he could read without effort”. Credit: Ferdinand Schmutzer/Public Domain*

In time, much of what Newton espoused would be proven wrong, thanks largely to Albert Einstein. With his General Theory of Relativity, Einstein would prove that time, distance and motion were not absolutes, but dependent on the observer. In so doing, he overturned one of the fundamental precepts of universal gravitation. Nevertheless, Einstein was one of Newton’s greatest admirers and acknowledged a great debt to his predecessor.

In addition to calling Newton a “shining spirit” (in a eulogy delivered in 1927 on the 200th anniversary of Newton’s death), Einstein also remarked that “Nature to him was an open book, whose letters he could read without effort.” On his study wall, Albert Einstein is said to have kept a picture of Newton, alongside pictures of Michael Faraday and James Clerk Maxwell.

A survey of Britain’s Royal Society was also conducted in 2005, where members were asked who had the greater effect on the history of science: Newton or Einstein. The majority of the Royal Society’s members agreed that overall, Newton had a greater impact on the sciences. Other polls conducted in recent decades have produced similar results, with Einstein and Newton vying for first and second place.

It is not easy thing to be living during one of the most auspicious times in history. Moreover, it is not easy in the midst of all of that to be blessed with an insight that will lead one to comes up with ideas that will revolutionize the sciences and forever alter the course of history. But throughout it all, Newton maintained a humble attitude, and summarized his accomplishments best with the famous words: “If I have seen further it is by standing on the shoulders of giants.^“

We have written many articles about Isaac Newton for Universe Today. Here’s an article about what Isaac Newton discovered, and here’s an article about the inventions of Isaac Newton.

Astronomy Cast also has a wonderful episode, titled Episode 275: Isaac Newton

For more information, check out this article from the Galileo Society on Isaac Newton, and the non-profit group known as The Newton Project.

We’ve also recorded an entire episode of Astronomy Cast all about Gravity. Listen here, Episode 102: Gravity.

September 27, 2015August 22, 2018 by Matt Williams

The Sun

This image from the Solar and Heliospheric Observatory (SOHO) Extreme ultraviolet Imaging Telescope (EIT) image shows large magnetically active regions and a pair of curving erupting prominences on June 28, 2000 during the current solar cycle 23 maximum. Prominences are huge clouds of relatively cool dense plasma suspended in the Sun's hot, thin corona. Magnetically active regions cause the principal total solar irradiance variations during each solar cycle. The hottest areas appear almost white, while the darker red areas indicate cooler temperatures. Credit: NASA & European Space Agency (ESA) — The Sun. Credit: NASA & European Space Agency (ESA)

The Sun is the center of the Solar System and the source of all life and energy here on Earth. It accounts for more than 99.86% of the mass of the Solar System and it’s gravity dominates all the planets and objects that orbit it. Since the beginning of history, human beings have understood the Sun’s importance to our world, it’s seasons, the diurnal cycle, and the life-cycle of plants.

Because of this, the Sun has been at the center of many ancient culture’s mythologies and systems of worship. From the Aztecs, Mayans and Incas to the ancient Sumerians, Egyptians, Greeks, Romans and Druids, the Sun was a central deity because it was seen as the bringer of all light and life. In time, our understanding of the Sun has changed and become increasingly empirical. But that has done nothing to diminish it’s significance.

Continue reading “The Sun”

June 6, 2015May 8, 2017 by Joshua Carroll

Mathematics: The Beautiful Language of the Universe

Let us discuss the very nature of the cosmos. What you may find in this discussion is not what you expect. Going into a conversation about the universe as a whole, you would imagine a story full of wondrous events such as stellar collapse, galactic collisions, strange occurrences with particles, and even cataclysmic eruptions of energy. You may be expecting a story stretching the breadth of time as we understand it, starting from the Big Bang and landing you here, your eyes soaking in the photons being emitted from your screen. Of course, the story is grand. But there is an additional side to this amazing assortment of events that oftentimes is overlooked; that is until you truly attempt to understand what is going on. Behind all of those fantastic realizations, there is a mechanism at work that allows for us to discover all that you enjoy learning about. That mechanism is mathematics, and without it the universe would still be shrouded in darkness. In this article, I will attempt to persuade you that math isn’t some arbitrary and sometimes pointless mental task that society makes it out to be, and instead show you that it is a language we use to communicate with the stars.

We are currently bound to our solar system. This statement is actually better than it sounds, as being bound to our solar system is one major step up from being bound simply to our planet, as we were

A defining moment for humanity: Galileo turing his spyglass towards the sky

before some very important minds elected to turn their geniuses toward the heavens. Before those like Galileo, who aimed his spyglass towards the sky, or Kepler discovering that planets move about the sun in ellipses, or Newton discovering a gravitational constant, mathematics was somewhat limited, and our understanding of the universe rather ignorant. At its core, mathematics allows a species bound to its solar system to probe the depths of the cosmos from behind a desk. Now, in order to appreciate the wonder that is mathematics, we must first step back and briefly look at its beginnings and how it is integrally tied into our very existence.

Mathematics almost certainly came about from very early human tribes (predating Babylonian culture which is attributed to some of the first organized mathematics in recorded history), that may have used math as a way of keeping track of lunar or solar cycles, and keeping count of animals, food and/or people by leaders. It is as natural as when you are a young child and you can see that you have

Ancient Babylonian tablet displaying early mathematics

one toy plus one other toy, meaning you have more than one toy. As you get older, you develop the ability to see that 1+1=2, and thus simple arithmetic seems to be interwoven into our very nature. Those that profess that they don’t have a mind for math are sadly mistaken because just as we all have a mind for breathing, or blinking, we all have this innate ability to understand arithmetic. Mathematics is both a natural occurrence and a human designed system. It would appear that nature grants us this ability to recognize patterns in the form of arithmetic, and then we systematically construct more complex mathematical systems that aren’t obvious in nature but let us further communicate with nature.

All this aside, mathematics developed alongside of human development, and carried on similarly with each culture that was developing it simultaneously. It’s a wonderful observation to see that cultures that had no contact with one another were developing similar mathematical constructs without conversing. However, it wasn’t until mankind decidedly turned their mathematical wonder towards the sky that math truly began to develop in an astonishing way. It is by no mere coincidence that our scientific revolution was spurred by the development of more advanced mathematics built not to tally sheep or people, but rather to further our understandings of our place within the universe. Once Galileo began measuring the rates at which objects fell in an attempt to show mathematically that the mass of an object had little to do with the speed in which it fell, mankind’s future would forever be altered.

This is where the cosmic perspective ties in to our want to further our mathematical knowledge. If it were not for math, we would still think we were on one of a few planets orbiting a star amidst the backdrop of seemingly motionless lights. This is a rather bleak outlook today compared to what we now know

Johannes Kepler used mathematics to model his observations of the planets.

about the awesomely large universe we reside in. This idea of the universe motivating us to understand more about mathematics can be inscribed in how Johannes Kepler used what he observed the planets doing, and then applied mathematics to it to develop a fairly accurate model (and method for predicting planetary motion) of the solar system. This is one of many demonstrations that illustrate the importance of mathematics within our history, especially within astronomy and physics.

The story of mathematics becomes even more amazing as we push forward to one of the most advanced thinkers humanity has ever known. Sir Isaac Newton, when pondering the motions of Halley’s Comet, came to the realization that the math that had been used thus far to describe physical motion of massive

bodies, simply would not suffice if we were to ever understand anything beyond that of our seemingly limited celestial nook. In a show of pure brilliance that lends validity to my earlier statement about how we can take what we naturally have and then construct a more complex system upon it, Newton developed the Calculus in which this way of approaching moving bodies, he was able to accurately model the motion of not only Halley’s comet, but also any other heavenly body that moved across the sky.

In one instant, our entire universe opened up before us, unlocking almost unlimited abilities for us to converse with the cosmos as never before. Newton also expanded upon what Kepler started. Newton recognized that Kepler’s mathematical equation for planetary motion, Kepler’s 3rd Law ( P²=A³ ), was purely based on empirical observation, and was only meant to measure what we observed within our solar system. Newton’s mathematical brilliance was in realizing that this basic equation could be made universal by applying a gravitational constant to the equation, in which gave birth to perhaps one of the most important equations to ever be derived by mankind; Newton’s Version of Kepler’s Third Law.

You can still see where Kepler's 3rd Law remains, but with the added values of the gravitational constant G, and M and m representing the masses of the two bodies in question, this equation is no longer restricted to just our solar system — You can still see where Kepler’s 3rd Law remains, but with the added values of the gravitational constant G, and M and m representing the masses of the two bodies in question, this equation is no longer restricted to just our solar system

What Newton realized was that when things move in non-linear ways, using basic Algebra would not produce the correct answer. Herein lays one of the main differences between Algebra and Calculus. Algebra allows one to find the slope (rate of change) of straight lines (constant rate of change), whereas Calculus allows one to find the slope of curved lines (variable rate of change). There are obviously many more applications of Calculus than just this, but I am merely illustrating a fundamental difference between the two in order to show you just how revolutionary this new concept was. All at once, the motions of planets and other objects that orbit the sun became more accurately measurable, and thus we gained the ability to understand the universe a little deeper. Referring back to Netwon’s Version of Kepler’s Third Law, we were now able to apply (and still do) this incredible physics equation to almost anything that is orbiting something else. From this equation, we can determine the mass of either of the objects, the distance apart they are from each other, the force of gravity that is exerted between the two, and other physical qualities built from these simple calculations.

With his understanding of mathematics, Newton was able to derive the aforementioned gravitational constant for all objects in the universe ( G = 6.672×10^-11 N m² kg^-2 ). This constant allowed him to unify astronomy and physics which then permitted predictions about how things moved in the universe. We could now measure the masses of planets (and the sun) more accurately, simply according to Newtonian physics (aptly named to honor just how important Newton was within physics and mathematics). We could now apply this newfound language to the cosmos, and begin coercing it to divulge its secrets. This was a defining moment for humanity, in that all of those things that prohibited our understandings prior to this new form of math were now at our fingertips, ready to be discovered. This is the brilliance of understanding Calculus, in that you are speaking the language of the stars.

There perhaps is no better illustration of the power that mathematics awarded us then in the discovery of the planet Neptune. Up until its discovery in September of 1846, planets were discovered simply by observing certain “stars” that were moving against the backdrop of all the other stars in odd ways. The term planet is Greek for “wanderer”, in that these peculiar stars wandered across the sky in noticeable patterns at different times of the year. Once the telescope was first turned upwards towards the sky by Galileo, these wanderers resolved into other worlds that appeared to be like ours. If fact, some of these worlds appeared to be little solar systems themselves, as Galileo discovered when he began recording the moons of Jupiter as they orbited around it.

After Newton presented his physics equations to the world, mathematicians were ready and excited to begin applying them to what we had been keeping track of for years. It was as if we were thirsty for the knowledge, and finally someone turned on the faucet. We began measuring the motions of the planets and gaining more accurate models for how they behaved. We used these equations to approximate the mass of the Sun. We were able to make remarkable predictions that were validated time and again simply by observation. What we were doing was unprecedented, as we were using mathematics to make almost impossible to know predictions that you would think we could never make without actually going to these planets, and then using actual observation to prove the math correct. However, what we also did was begin to figure out some odd discrepancies with certain things. Uranus, for instance, was behaving not as it should according to Newton’s laws.

Here you can see that the inner planet is being perturbed by the outer planet, in our situation, that outer planet was Neptune, not yet discovered. — Here you can see that the inner planet is being perturbed by the outer planet. In our situation, that outer planet was Neptune, which had yet to be discovered.

What makes the discovery of Neptune so wonderful was the manner in which it was discovered. What Newton had done was uncover a deeper language of the cosmos, in which the universe was able to reveal more to us. And this is exactly what happened when we applied this language to the orbit of Uranus. The manner in which Uranus orbited was curious and did not fit what it should have if it was the only planet that far out from the sun. Looking at the numbers, there had to be something else out there perturbing its orbit. Now, before Newton’s mathematical insights and laws, we would have had no reason to suspect anything was wrong in what we observed. Uranus orbited in the way Uranus orbited; it was just how it was. But, again revisiting that notion of mathematics being an ever increasing dialogue with the universe, once we asked the question in the right format, we realized that there really must be something else beyond what we couldn’t see. This is the beauty of mathematics writ large; an ongoing conversation with the universe in which more than we may expect is revealed.

It came to a French mathematician Urbain Le Verrier who sat down and painstakingly worked through the mathematical equations of the orbit of Uranus. What he was doing was using Newton’s mathematical equations backwards, realizing that there must be an object out there beyond the orbit of Uranus that was also orbiting the sun,

French mathematician who discovered the planet Neptune by using only mathematics

and then looking to apply the right mass and distance that this unseen object required for perturbing the orbit of Uranus in the way we were observing it was. This was phenomenal, as we were using parchment and ink to find a planet that nobody had ever actually observed. What he found was that an object, soon to be Neptune, had to be orbiting at a specific distance from the sun, with the specific mass that would cause the irregularities in the orbital path of Uranus. Confident of his mathematical calculations, he took his numbers to the New Berlin Observatory, where the astronomer Johann Gottfried Galle looked exactly where Verrier’s calculations told him to look, and there lay the 8th and final planet of our solar system, less than 1 degree off from where Verrier’s calculations said for him to look. What had just happened was an incredible confirmation of Newton’s gravitational theory and proved that his mathematics were correct.

Are There Oceans on Neptune — Neptune is more than just the 8th planet in our solar system; it is a celestial reminder of the power that mathematics grants us.

These types of mathematical insights continued on long after Newton. Eventually, we began to learn much more about the universe with the advent of better technology (brought about by advances in mathematics). As we moved into the 20th century, quantum theory began to take shape, and we soon realized that Newtonian physics and mathematics seemed to hold no sway over what we observed on the quantum level. In another momentous event in human history, yet again brought forth by the advancement in mathematics, Albert Einstein unveiled his theories of General and Special Relativity, which was a new way to look not only at gravity, but

Einstein's Relativity, yet another momentous advancement for humanity brought forth from an ongoing mathematical dialogue. Image via Pixabay. — Einstein’s equation for the energy-mass equivalency, yet another incredible advancement for humanity brought forth from an ongoing mathematical dialogue. Image via Pixabay.

also on energy and the universe in general. What Einstein’s mathematics did was allow for us to yet again uncover an even deeper dialogue with the universe, in which we began to understand its origins.

Continuing this trend of advancing our understandings, what we have realized is that now there are two sects of physics that do not entirely align. Newtonian or “classical” physics, that works extraordinarily well with the very large (motions of planets, galaxies, etc…) and quantum physics that explains the extremely small (the interactions of sub-atomic particles, light, etc…). Currently, these two areas of physics are not in alignment, much like two different dialects of a language. They are similar and they both work, but they are not easily reconcilable with one another. One of the greatest challenges we face today is attempting to create a mathematical grand “theory of everything” which either unites the laws in the quantum world with that of the macroscopic world, or to work to explain everything solely in terms of quantum mechanics. This is no easy task, but we are striving forward nonetheless.

As you can see, mathematics is more than just a set of vague equations and complex rules that you are required to memorize. Mathematics is the language of the universe, and in learning this language, you are opening yourself up the core mechanisms by which the cosmos operates. It is the same as traveling to a new land, and slowly picking up on the native language so that you may begin to learn from them. This mathematical endeavor is what allows us, a species bound to our solar system, to explore the depths of the universe. As of now, there simply is no way for us to travel to the center of our galaxy and observe the supermassive black hole there to visually confirm its existence. There is no way for us to venture out into a Dark Nebula and watch in real time a star being born. Yet, through mathematics, we are able to understand how these things exist and work. When you set about to learn math, you are not only expanding your mind, but you are connecting with the universe on a fundamental level. You can, from your desk, explore the awesome physics at the event horizon of a black hole, or bear witness to the destructive fury behind a supernova. All of those things that I mentioned at the beginning of this article come into focus through mathematics. The grand story of the universe is written in mathematics, and our ability to translate those numbers into the events that we all love to learn about is nothing short of amazing. So remember, when you are presented with the opportunity to learn math, accept every bit of it because math connects us to the stars.

We are connected to the universe through mathematics... — We are connected to the universe through mathematics…

February 13, 2015December 23, 2015 by Matt Williams

What is Hooke’s Law?

The spring is a marvel of human engineering and creativity. For one, it comes in so many varieties – the compression spring, the extension spring, the torsion spring, the coil spring, etc. – all of which serve different and specific functions. These functions in turn allow for the creation of many man-made objects, most of which emerged as part of the Scientific Revolution during the late 17th and 18th centuries.

As an elastic object used to store mechanical energy, the applications for them are extensive, making possible such things as an automotive suspension systems, pendulum clocks, hand sheers, wind-up toys, watches, rat traps, digital micromirror devices, and of course, the Slinky.

Like so many other devices invented over the centuries, a basic understanding of the mechanics is required before it can so widely used. In terms of springs, this means understanding the laws of elasticity, torsion and force that come into play – which together are known as Hooke’s Law.

Hooke’s Law is a principle of physics that states that the that the force needed to extend or compress a spring by some distance is proportional to that distance. The law is named after 17th century British physicist Robert Hooke, who sought to demonstrate the relationship between the forces applied to a spring and its elasticity.

*Illustration of Hooke’s Law, showing the relationship between force and distance when applied to a spring. Credit: GSU/hyperphysics*

He first stated the law in 1660 as a Latin anagram, and then published the solution in 1678 as ut tensio, sic vis – which translated, means “as the extension, so the force” or “the extension is proportional to the force”).

This can be expressed mathematically as F= -kX, where F is the force applied to the spring (either in the form of strain or stress); X is the displacement of the spring, with a negative value demonstrating that the displacement of the spring once it is stretched; and k is the spring constant and details just how stiff it is.

Hooke’s law is the first classical example of an explanation of elasticity – which is the property of an object or material which causes it to be restored to its original shape after distortion. This ability to return to a normal shape after experiencing distortion can be referred to as a “restoring force”. Understood in terms of Hooke’s Law, this restoring force is generally proportional to the amount of “stretch” experienced.

In addition to governing the behavior of springs, Hooke’s Law also applies in many other situations where an elastic body is deformed. These can include anything from inflating a balloon and pulling on a rubber band to measuring the amount of wind force is needed to make a tall building bend and sway.

Illustration from Hooke's 1678 treaties "De potentia restitutiva (Of Spring)" Credit: umn.edu/ — Illustration from Hooke’s 1678 treaties “De potentia restitutiva (Of Spring)” Credit: umn.edu/

This law has had many important practical applications, with one being the creation of a balance wheel, which made possible the creation of the mechanical clock, the portable timepiece, the spring scale and the manometer (aka. the pressure gauge). Also, because it is a close approximation of all solid bodies (as long as the forces of deformation are small enough), numerous branches of science and engineering as also indebted to Hooke for coming up with this law. These include the disciplines of seismology, molecular mechanics and acoustics.

However, like most classical mechanics, Hooke’s Law only works within a limited frame of reference. Because no material can be compressed beyond a certain minimum size (or stretched beyond a maximum size) without some permanent deformation or change of state, it only applies so long as a limited amount of force or deformation is involved. In fact, many materials will noticeably deviate from Hooke’s law well before those elastic limits are reached.

Still, in its general form, Hooke’s Law is compatible with Newton’s laws of static equilibrium. Together, they make it possible to deduce the relationship between strain and stress for complex objects in terms of the intrinsic materials of the properties it is made of. For example, one can deduce that a homogeneous rod with uniform cross section will behave like a simple spring when stretched, with a stiffness (k) directly proportional to its cross-section area and inversely proportional to its length.

Balance wheel in a cheap 1950s alarm clock, the Apollo, by Lux Mfg. Co. showing the balance spring (1) and regulator (2). Credit: Wikipedia/public domain. — *The balance wheel in a cheap 1950s alarm clock (the Apollo, by Lux Mfg. Co.) showing the balance wheel (1) and regulator (2). Credit: Wikipedia/Public Domain*

Another interesting thing about Hooke’s law is that it is a a perfect example of the First Law of Thermodynamics. Any spring when compressed or extended almost perfectly conserves the energy applied to it. The only energy lost is due to natural friction.

In addition, Hooke’s law contains within it a wave-like periodic function. A spring released from a deformed position will return to its original position with proportional force repeatedly in a periodic function. The wavelength and frequency of the motion can also be observed and calculated.

The modern theory of elasticity is a generalized variation on Hooke’s law, which states that the strain/deformation of an elastic object or material is proportional to the stress applied to it. However, since general stresses and strains may have multiple independent components, the “proportionality factor” may no longer be just a single real number.

A good example of this would be when dealing with wind, where the stress applied varies in intensity and direction. In cases like these, it is best to employ a linear map (aka. a tensor) that can be represented by a matrix of real numbers instead of a single value.

If you enjoyed this article there are several others that you will enjoy on Universe Today. Here is one about Sir Isaac Newton’s contributions to the many fields of science. Here is an interesting article about gravity.

There are also some great resources online, such as this lecture on Hooke’s Law that you can watch on academicearth.org. There is also a great explanation of elasticity on howstuffworks.com.

You can also listen to Episode 138, Quantum Mechanics from Astronomy Cast for more information.

Sources:
Hyperphysics
Physics 24/7

January 30, 2014January 6, 2016 by Brian Koberlein

How We Know Gravity is Not (Just) a Force

This artist’s impression shows the exotic double object that consists of a tiny, but very heavy neutron star that spins 25 times each second, orbited every two and a half hours by a white dwarf star. The neutron star is a pulsar named PSR J0348+0432 that is giving off radio waves that can be picked up on Earth by radio telescopes. Although this unusual pair is very interesting in its own right it is also a unique laboratory for testing the limits of physical theories. This system is radiating gravitational radiation, ripples in spacetime. Although these waves cannot be yet detected directly by astronomers on Earth they can be detected indirectly by measuring the change in the orbit of the system as it loses energy. As the pulsar is so small the relative sizes of the two objects are not drawn to scale.

When we think of gravity, we typically think of it as a force between masses. When you step on a scale, for example, the number on the scale represents the pull of the Earth’s gravity on your mass, giving you weight. It is easy to imagine the gravitational force of the Sun holding the planets in their orbits, or the gravitational pull of a black hole. Forces are easy to understand as pushes and pulls.

But we now understand that gravity as a force is only part of a more complex phenomenon described the theory of general relativity. While general relativity is an elegant theory, it’s a radical departure from the idea of gravity as a force. As Carl Sagan once said, “Extraordinary claims require extraordinary evidence,” and Einstein’s theory is a very extraordinary claim. But it turns out there are several extraordinary experiments that confirm the curvature of space and time.

The key to general relativity lies in the fact that everything in a gravitational field falls at the same rate. Stand on the Moon and drop a hammer and a feather, and they will hit the surface at the same time. The same is true for any object regardless of its mass or physical makeup, and this is known as the equivalence principle.

Since everything falls in the same way regardless of its mass, it means that without some external point of reference, a free-floating observer far from gravitational sources and a free-falling observer in the gravitational field of a massive body each have the same experience. For example, astronauts in the space station look as if they are floating without gravity. Actually, the gravitational pull of the Earth on the space station is nearly as strong as it is at the surface. The difference is that the space station (and everything in it) is falling. The space station is in orbit, which means it is literally falling around the Earth.

The International Space Station orbiting Earth. Credit: NASA

This equivalence between floating and falling is what Einstein used to develop his theory. In general relativity, gravity is not a force between masses. Instead gravity is an effect of the warping of space and time in the presence of mass. Without a force acting upon it, an object will move in a straight line. If you draw a line on a sheet of paper, and then twist or bend the paper, the line will no longer appear straight. In the same way, the straight path of an object is bent when space and time is bent. This explains why all objects fall at the same rate. The gravity warps spacetime in a particular way, so the straight paths of all objects are bent in the same way near the Earth.

So what kind of experiment could possibly prove that gravity is warped spacetime? One stems from the fact that light can be deflected by a nearby mass. It is often argued that since light has no mass, it shouldn’t be deflected by the gravitational force of a body. This isn’t quite correct. Since light has energy, and by special relativity mass and energy are equivalent, Newton’s gravitational theory predicts that light would be deflected slightly by a nearby mass. The difference is that general relativity predicts it will be deflected twice as much.

Description of Eddington's experiment from the Illustrated London News (1919). — Description of Eddington’s experiment from the Illustrated London News (1919).

The effect was first observed by Arthur Eddington in 1919. Eddington traveled to the island of Principe off the coast of West Africa to photograph a total eclipse. He had taken photos of the same region of the sky sometime earlier. By comparing the eclipse photos and the earlier photos of the same sky, Eddington was able to show the apparent position of stars shifted when the Sun was near. The amount of deflection agreed with Einstein, and not Newton. Since then we’ve seen a similar effect where the light of distant quasars and galaxies are deflected by closer masses. It is often referred to as gravitational lensing, and it has been used to measure the masses of galaxies, and even see the effects of dark matter.

Another piece of evidence is known as the time-delay experiment. The mass of the Sun warps space near it, therefore light passing near the Sun is doesn’t travel in a perfectly straight line. Instead it travels along a slightly curved path that is a bit longer. This means light from a planet on the other side of the solar system from Earth reaches us a tiny bit later than we would otherwise expect. The first measurement of this time delay was in the late 1960s by Irwin Shapiro. Radio signals were bounced off Venus from Earth when the two planets were almost on opposite sides of the sun. The measured delay of the signals’ round trip was about 200 microseconds, just as predicted by general relativity. This effect is now known as the Shapiro time delay, and it means the average speed of light (as determined by the travel time) is slightly slower than the (always constant) instantaneous speed of light.

A third effect is gravitational waves. If stars warp space around them, then the motion of stars in a binary system should create ripples in spacetime, similar to the way swirling your finger in water can create ripples on the water’s surface. As the gravity waves radiate away from the stars, they take away some of the energy from the binary system. This means that the two stars gradually move closer together, an effect known as inspiralling. As the two stars inspiral, their orbital period gets shorter because their orbits are getting smaller.

Decay of pulsar period compared to prediction (dashed curve). Data from Hulse and Taylor, Plotted by the author.

For regular binary stars this effect is so small that we can’t observe it. However in 1974 two astronomers (Hulse and Taylor) discovered an interesting pulsar. Pulsars are rapidly rotating neutron stars that happen to radiate radio pulses in our direction. The pulse rate of pulsars are typically very, very regular. Hulse and Taylor noticed that this particular pulsar’s rate would speed up slightly then slow down slightly at a regular rate. They showed that this variation was due to the motion of the pulsar as it orbited a star. They were able to determine the orbital motion of the pulsar very precisely, calculating its orbital period to within a fraction of a second. As they observed their pulsar over the years, they noticed its orbital period was gradually getting shorter. The pulsar is inspiralling due to the radiation of gravity waves, just as predicted.

Illustration of Gravity Probe B. Credit: Gravity Probe B Team, Stanford, NASA

Finally there is an effect known as frame dragging. We have seen this effect near Earth itself. Because the Earth is rotating, it not only curves spacetime by its mass, it twists spacetime around it due to its rotation. This twisting of spacetime is known as frame dragging. The effect is not very big near the Earth, but it can be measured through the Lense-Thirring effect. Basically you put a spherical gyroscope in orbit, and see if its axis of rotation changes. If there is no frame dragging, then the orientation of the gyroscope shouldn’t change. If there is frame dragging, then the spiral twist of space and time will cause the gyroscope to precess, and its orientation will slowly change over time.

results_graph-lg — Gravity Probe B results. Credit: Gravity Probe B team, NASA.

We’ve actually done this experiment with a satellite known as Gravity Probe B, and you can see the results in the figure here. As you can see, they agree very well.

Each of these experiments show that gravity is not simply a force between masses. Gravity is instead an effect of space and time. Gravity is built into the very shape of the universe.

Think on that the next time you step onto a scale.

July 4, 2011October 18, 2016 by Matt Williams

What is Absolute Space?

The explosion in the sciences that took place in the 17th and 18th centuries revolutionized not only the way we think of our world, but of time and space itself. Much of this is owed to individuals like Sir Isaac Newton, a man whose theories came to form the basis of modern physics. Though much of his theories would later come to be challenged with the discovery of relativity and quantum mechanics, they were nonetheless extremely influential because they gave later generations a framework. It is to him, for example, that we are indebted for the notions of Absolute Time and Absolute Space, and how the two were thought to be separate aspects of objective reality.
In his magnum opus, PhilosophiæNaturalis Principia Mathematica (Mathematical Principles for Natural Philosophy), Newton laid the groundwork for the concept of Absolute Space thusly:

“Absolute space, in its own nature, without regard to anything external, remains always similar and immovable. Relative space is some movable dimension or measure of the absolute spaces; which our senses determine by its position to bodies: and which is vulgarly taken for immovable space … Absolute motion is the translation of a body from one absolute place into another: and relative motion, the translation from one relative place into another.”

In other words, Absolute Space is the study of space as an absolute, unmoving reference point for what inertial systems (i.e. planets and other objects) exist within it. Thus, every object has an absolute state of motion relative to absolute space, so that an object must be either in a state of absolute rest, or moving at some absolute speed.

These views were controversial even in Newton’s own time. However, it was with the advent of modern physics and the Theory of Special Relativity, that much of the basis for Newtonian physics would come to be shattered. In essence, special relativity proposed that time and space are not independent realities but different expressions of the same thing. In this model, time and motion are dependent on the observer and there is no fixed point of reference, only relative forms of motion which are determined by comparing them to other points of reference.

However, it would be fair to say that it was Newton’s own definitions of space and time as independent phenomena that allowed for the development of physics as we know it today. By giving physicists clear definitions to work with and challenge, later generations of scientists like Einstein were able to express clearly how space was not absolute since it itself was always in motion, and how one could not divorce space from time.

We have written many articles about absolute space for Universe Today. Here’s an article about what is space, and here’s an article about how cold space is.

If you’d like more info on absolute space, check out an article about Isaac Newton’s “Absolute Space”. Also, here’s an article about Absolute Time and Space.

We’ve also recorded an entire episode of Astronomy Cast all about Space Elevators. Listen here, Episode 144: Space Elevators.

Sources:
http://en.wikipedia.org/wiki/Absolute_time_and_space
http://en.wikipedia.org/wiki/Sir_Isaac_Newton
http://plato.stanford.edu/entries/newton-stm/
http://en.wikipedia.org/wiki/Special_relativity
http://novan.com/spcenrgy.htm

December 10, 2010September 25, 2016 by Jerry Coffey

What did Isaac Newton Invent?

Isaac Newton, Father of Classical Mechanics

Sir Issac Newton is best know for his laws of motion. Many people’s knowledge of his scientific contributions stops there. Issac Newtons inventions contributed a great deal to our current understanding of subjects from optics to theology and how early scientists were able to view their world.

In mathematics Isaac Newton inventions included laying the ground work for differential and integral calculus. His work was based on his insight that the integration of a function is merely the inverse procedure to differentiating it. Taking differentiation as the basic operation, he produced simple analytical methods that unified many separate techniques previously developed to solve apparently unrelated problems such as finding areas, tangents, the lengths of curves and the maxima and minima of functions.

Issac Newton inventions in mechanics and gravitation were summarized the Principia. His discoveries in terrestrial and celestial mechanics showed how universal gravitation provided an explanation of falling bodies on Earth and of the motions of planets, comets, and other bodies in the heavens. He explained a wide range of then unrelated phenomena: the eccentric orbits of comets, the tides and their variations, the precession of the Earth’s axis, and motion of the Moon as perturbed by the gravity of the Sun. This work includes Newton’s three famous laws of motion, fluid motion, and an explanation of Kepler’s laws of planetary motion.

Isaac Newton inventions in optics included his observation that white light could be separated by a prism into a spectrum of different colors, each characterized by a unique refractivity. He proposed the corpuscular theory of light. He was the first person to understand the rainbow. He was the first person to use a curved mirror in a telescope to prevent light form being broken up into unwanted colors.

Isaac Newton inventions and contributions to science were many and varied. They covered revolutionary ideas and practical inventions. His works in physics, mathematics and astronomy are still important today. His contributions in any one of these fields would have made him famous; taken as a whole, they make him truly outstanding.

We have written many articles about Isaac Newton’s inventions for Universe Today. Here’s an article about celestial mechanics, and here’s an article about Newton’s laws of motion.

If you’d like more info on Isaac Newton’s inventions, check out How Stuff Works for an interesting article about Isaac Newton’s inventions, and here’s a link to Isaac Newton’s Biography.

We’ve also recorded an entire episode of Astronomy Cast all about Gravity. Listen here, Episode 102: Gravity.

Sources:
How Stuff Works
University of Virginia
NASA

May 10, 2010December 24, 2015 by Nancy Atkinson

Newton’s Apple Tree to Defy Gravity on Upcoming Shuttle Mission

The STS-132 crew arrived Monday evening at Kennedy Space Center. Image credit: Alan Walters (awaltersphoto.com) for Universe Today.

[/caption]
As the space shuttle crew arrived at Kennedy Space Center for Thursday’s scheduled launch of the STS-132 mission, already on board space shuttle Atlantis is a piece of physicist Sir Isaac Newton’s apple tree. A 4-inch-long wood sample from the original tree that supposedly inspired Newton’s theory of gravity, along with a picture of Newton, will be taken into orbit by British-born astronaut Piers Sellers, a member of the crew for this next mission to the International Space Station. The wood is part of the collection of the Royal Society archives in London, and will be returned there following the flight. “We’re delighted to take this piece of Sir Isaac Newton’s apple tree to orbit,” said Sellers in an article from AFP. “While it’s up there, it will be experiencing no gravity, so if it had an apple on it, the apple wouldn’t fall.”

*Of course, that is not quite correct.

The piece of Newton’s tree is will still be experiencing gravity, and in fact, will be falling the entire time it is in orbit. It will be in free fall along with the shuttle and space station as it orbits the Earth. A free-falling object falls under the sole influence of gravity, and in the case of the shuttle (or any object in orbit), its orbital motion keeps it moving fast enough that it doesn’t fall back to Earth — unless its acceleration changes.

Continue reading “Newton’s Apple Tree to Defy Gravity on Upcoming Shuttle Mission”

July 19, 2009October 18, 2016 by John Carl Villanueva

What is the Gravitational Constant?

Visualization of a massive body generating gravitational waves (UWM)

The gravitational constant is the proportionality constant used in Newton’s Law of Universal Gravitation, and is commonly denoted by G. This is different from g, which denotes the acceleration due to gravity. In most texts, we see it expressed as:

G = 6.673×10^-11 N m² kg^-2

It is typically used in the equation:

F = (G x m₁ x m₂) / r² , wherein

F = force of gravity

G = gravitational constant

m₁ = mass of the first object (lets assume it’s of the massive one)

m₂ = mass of the second object (lets assume it’s of the smaller one)

r = the separation between the two masses

As with all constants in Physics, the gravitational constant is an empirical value. That is to say, it is proven through a series of experiments and subsequent observations.

Although the gravitational constant was first introduced by Isaac Newton as part of his popular publication in 1687, the Philosophiae Naturalis Principia Mathematica, it was not until 1798 that the constant was observed in an actual experiment. Don’t be surprised. It’s mostly like this in physics. The mathematical predictions normally precede the experimental proofs.

Anyway, the first person who successfully measured it was the English physicist, Henry Cavendish, who measured the very tiny force between two lead masses by using a very sensitive torsion balance. It should be noted that, after Cavendish, although there have been more accurate measurements, the improvements on the values (i.e., being able to obtain values closer to Newton’s G) have not been really substantial.

Looking at the value of G, we see that when we multiply it with the other quantities, it results in a rather small force. Let’s expand that value to give you a better idea on how small it really is: 0.00000000006673 N m² kg^-2

Alright, let’s now see what force would two 1-kg objects exert on one another when their geometrical centers are spaced 1 meter apart. So, how much do we get?

F = 0.00000000006673 N. It really doesn’t matter much if we increase both masses substantially.

For example, let’s try the heaviest recorded mass of an elephant, 12,000 kg. Assuming we have two of these, spaced 1 meter apart from their centers. I know it’s difficult to imagine that since elephants are rather stout, but let’s just proceed this way because I want to put emphasis on the significance of G.

So, how much did we get? Even if we rounded that off, we’d still obtain only 0.01 N. For comparison, the force exerted by the earth on an apple is roughly 1 N. No wonder we don’t feel any force of attraction when we sit beside someone… unless of course you’re a male and that person is Megan Fox (still, it’d be safe to assume that the attraction would only be one way).

Therefore, the force of gravity is only noticeable when we consider at least one mass to be very massive, e.g. a planet’s.

Allow me to end this discussion with one more mathematical exercise. Assuming you know both your mass and your weight, and you know the radius of the earth. Plug those into the equation above and solve for the other mass. Voila! Wonder of wonders, you’ve just obtained the mass of the Earth.

You can read more about the gravitational constant here in Universe Today. Want to learn more about a new study that finds fundamental force hasn’t changed over time? There’s also some insights you can find among the comments in this article: Record Breaking “Dark Matter Web” Structures Observed Spanning 270 Million Light Years Across

There’s more about it at NASA. Here are a couple of sources there:

Here are two episodes at Astronomy Cast that you might want to check out as well:

Sources: