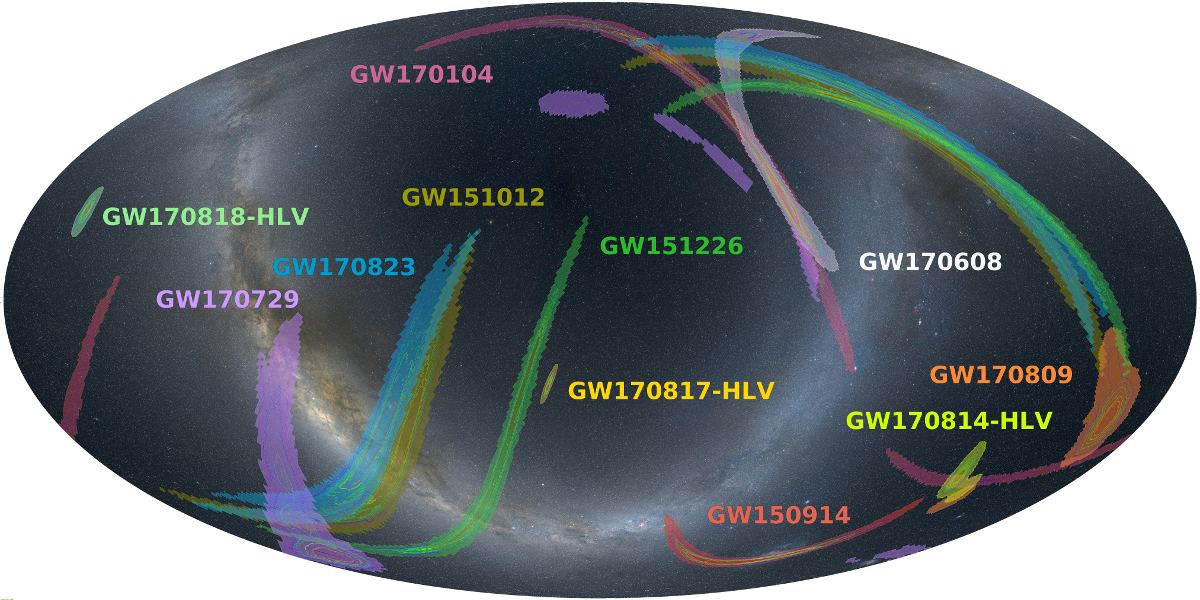
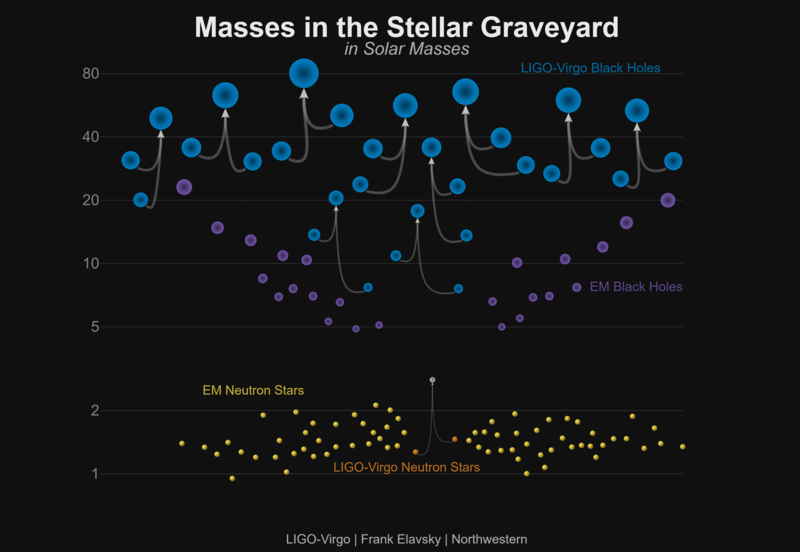
Gravitational Waves Archives

June 17, 2020June 17, 2020 by Evan Gough

Why Pulsars Are So Bright

Pulsars are fast-spinning neutron stars that emit narrow, sweeping beams of radio waves. A new study identifies the origin of those radio waves. NASA’s Goddard Space Flight Center

When pulsars were first discovered in 1967, their rhythmic radio-wave pulsations were a mystery. Some thought their radio beams must be of extraterrestrial origin.

We’ve learned a lot since then. We know that pulsars are magnetized, rotating neutrons stars. We know that they rotate very rapidly, with their magnetic poles sending sweeping beams of radio waves out into space. And if they’re aimed the right way, we can “see” them as pulses of radio waves, even though the radio waves are steady. They’re kind of like lighthouses.

But the exact mechanism that creates all of that electromagnetic radiation has remained a mystery.

June 2, 2020June 2, 2020 by Evan Gough

New Simulations Show How Black Holes Grow, Through Mergers and Accretion

Artist's impression of two merging black holes. Credit: Bohn, Throwe, Hébert, Henriksson, Bunandar, Taylor, Scheel/SXS

One of the most pressing questions in astronomy concerns black holes. We know that massive stars that explode as supernovae can leave stellar mass black holes as remnants. And astrophysicists understand that process. But what about the supermassive black holes (SMBHs) like Sagittarius A-star (Sgr A*,) at the heart of the Milky Way?

SMBHs can have a billion solar masses. How do they get so big?

April 22, 2020April 22, 2020 by Matt Williams

Astronomers Detected a Black Hole Merger With Very Different Mass Objects

Still image from a numerical simulation of an unequal mass binary black hole merger, with parameters consistent with GW190412. [Image credit: N. Fischer, H. Pfeiffer, A. Buonanno (Max Planck Institute for Gravitational Physics), Simulating eXtreme Spacetimes project]

In another first, scientists at the LIGO and Virgo gravitational wave detectors announced a signal unlike anything they’ve ever seen before. While many black hole mergers have been detected thanks to LIGO and Virgo’s international network for detectors, this particular signal (GW190412) was the first where the two black holes had distinctly different masses.

March 23, 2020 by Matt Williams

NASA Chooses 4 New Astronomy Space Missions for Additional Study

Hot stars burn brightly in this image from NASA's Galaxy Evolution Explorer, showing the ultraviolet side of a familiar face. At approximately 2.5 million light-years away, the Andromeda galaxy, or M31, is our Milky Way's largest galactic neighbor. The entire galaxy spans 260,000 light-years across -- a distance so large, it took 11 different image segments stitched together to produce this view of the galaxy next door. The bands of blue-white making up the galaxy's striking rings are neighborhoods that harbor hot, young, massive stars. Dark blue-grey lanes of cooler dust show up starkly against these bright rings, tracing the regions where star formation is currently taking place in dense cloudy cocoons. Eventually, these dusty lanes will be blown away by strong stellar winds, as the forming stars ignite nuclear fusion in their cores. Meanwhile, the central orange-white ball reveals a congregation of cooler, old stars that formed long ago. When observed in visible light, Andromeda's rings look more like spiral arms. The ultraviolet view shows that these arms more closely resemble the ring-like structure previously observed in infrared wavelengths with NASA's Spitzer Space Telescope. Astronomers using Spitzer interpreted these rings as evidence that the galaxy was involved in a direct collision with its neighbor, M32, more than 200 million years ago. Andromeda is so bright and close to us that it is one of only ten galaxies that can be spotted from Earth with the naked eye. This view is two-color composite, where blue represents far-ultraviolet light, and orange is near-ultraviolet light.

Since 1958, the NASA Explorer Program has conducted low-cost missions that were deemed relevant to the goals of the Science Mission Directorate (SMD), particularly where the study of our Sun and the deeper cosmic mysteries are concerned. Recently, the Explorer Program selected four missions that they considered to be well-suited to these goals, two of which will be selected for launch in the coming years.

Consisting of two astrophysics Small Explorer (SMEX) and two Missions of Opportunity (MO) proposals, these missions are designed to study cosmic explosions and the debris they leave behind, as well as monitor how nearby stellar flares may affect the atmospheres of orbiting planets. After detailed evaluations, two of these missions will be selected next year and will take to space sometime in 2025.

February 5, 2020February 5, 2020 by Evan Gough

14% of all the Massive Stars in the Universe are Destined to Collide as Black Holes

This illustration shows the merger of two black holes and the gravitational waves that ripple outward as the black holes spiral toward each other. Could black holes like these (which represent those detected by LIGO on Dec. 26, 2015) collide in the dusty disk around a quasar's supermassive black hole explain gravitational waves, too? Credit: LIGO/T. Pyle — This illustration shows the merger of two supermassive black holes and the gravitational waves that ripple outward as the black holes spiral toward each other. Credit: LIGO/T. Pyle

Einstein’s Theory of General Relativity predicted that black holes would form and eventually collide. It also predicted the creation of gravitational waves from the collision. But how often does this happen, and can we calculate how many stars this will happen to?

A new study from a physicist at Vanderbilt University sought to answer these questions.

January 17, 2020January 17, 2020 by Evan Gough

A Mysterious Burst of Gravitational Waves Came From a Region Near Betelgeuse. But There’s Probably No Connection

Betelgeuse was the first star directly imaged -- besides our own Sun, of course. Image obtained by the Hubble Space Telescope. Credit: Andrea Dupree (Harvard-Smithsonian CfA), Ronald Gilliland (STScI), NASA and ESA

Gravitational waves are caused by calamitous events in the Universe. Neutron stars that finally merge after circling each other for a long time can create them, and so can two black holes that collide with each other. But sometimes there’s a burst of gravitational waves that doesn’t have a clear cause.

September 24, 2019March 2, 2020 by Matt Williams

Just How Feasible is a Warp Drive?

Artist's impression of the IXS Enterprise, a warp ship. Credit: Mark Rademaker

It’s hard living in a relativistic Universe, where even the nearest stars are so far away and the speed of light is absolute. It is little wonder then why science fiction franchises routinely employ FTL (Faster-than-Light) as a plot device. Push a button, press a pedal, and that fancy drive system – whose workings no one can explain – will send us to another location in space-time.

However, in recent years, the scientific community has become understandably excited and skeptical about claims that a particular concept – the Alcubierre Warp Drive – might actually be feasible. This was the subject of a presentation made at this year’s American Institute of Aeronautics and Astronautics Propulsion and Energy Forum, which took place from August 19th to 22nd in Indianapolis.

September 9, 2019September 10, 2019 by Matt Williams

Gravitational Wave Detectors Might be Able to Detect Dark Matter Particles Colliding With Their Mirrors

The early universe. Credit: Tom Abel & Ralf Kaehler (KIPACSLAC)/ AMNH/NASA

The field of astronomy has been revolutionized thanks to the first-ever detection of gravitational waves (GWs). Since the initial detection was made in February of 2016 by scientists at the Laser Interferometer Gravitational-wave Observatory (LIGO), multiple events have been detected. These have provided insight into a phenomenon that was predicted over a century ago by Albert Einstein.

As it turns out, the infrastructure that is used to detect GWs could also help crack another astronomical mystery: Dark Matter! According to a new study by a team of Japanese researchers, laser interferometers could be used to look for Weakly-Interacting Massive Particles (WIMPs), a major candidate particle in the hunt for Dark Matter.

May 2, 2019May 5, 2019 by Evan Gough

It Looks Like LIGO/Virgo Have Detected a Black Hole Eating a Neutron Star. For the First Time Ever

A new signal detected by LIGO/Virgo may be the so-called ‘holy grail’ of astrophysics: the merger of a neutron star and a black hole. They’ve discovered pairs of black holes merging, and pairs of neutron stars merging, but until now, not a neutron star-black hole pair.

April 25, 2019April 27, 2019 by Matt Williams

As Expected, the Newly Upgraded LIGO is Finding a Black Hole Merger Every Week

In February 2016, LIGO detected gravity waves for the first time. As this artist's illustration depicts, the gravitational waves were created by merging black holes. The third detection just announced was also created when two black holes merged. Credit: LIGO/A. Simonnet. — Artist's impression of merging binary black holes. Credit: LIGO/A. Simonnet.

In February of 2016, scientists at the Laser Interferometer Gravitational-wave Observatory (LIGO) announced the first-ever detection of gravitational waves (GWs). Since then, multiple events have been detected, providing insight into a cosmic phenomena that was predicted over a century ago by Einstein’s Theory of General Relativity.

A little over a year ago, LIGO was taken offline so that upgrades could be made to its instruments, which would allow for detections to take place “weekly or even more often.” After completing the upgrades on April 1st, the observatory went back online and performed as expected, detecting two probable gravitational wave events in the space of two weeks.