Posted on by Shannon Hall

Surprise! Classical Novae Produce Gamma Rays

These images show Fermi data centered on each of the four gamma-ray novae observed by the LAT. Colors indicate the number of detected gamma rays with energies greater than 100 million electron volts (blue indicates lowest, yellow highest). Image Credit: NASA/DOE/Fermi LAT Collaboration

In a classical nova, a white dwarf siphons material off a companion star, building up a layer on its surface until the temperature and pressure are so high (a process which can take tens of thousands of years) that its hydrogen begins to undergo nuclear fusion, triggering a runaway reaction that detonates the accumulated gas.

The bright outburst, which releases up to 100,000 times the annual energy output of our Sun, can blaze for months. All the while, the white dwarf remains intact, with the potential of going nova again.

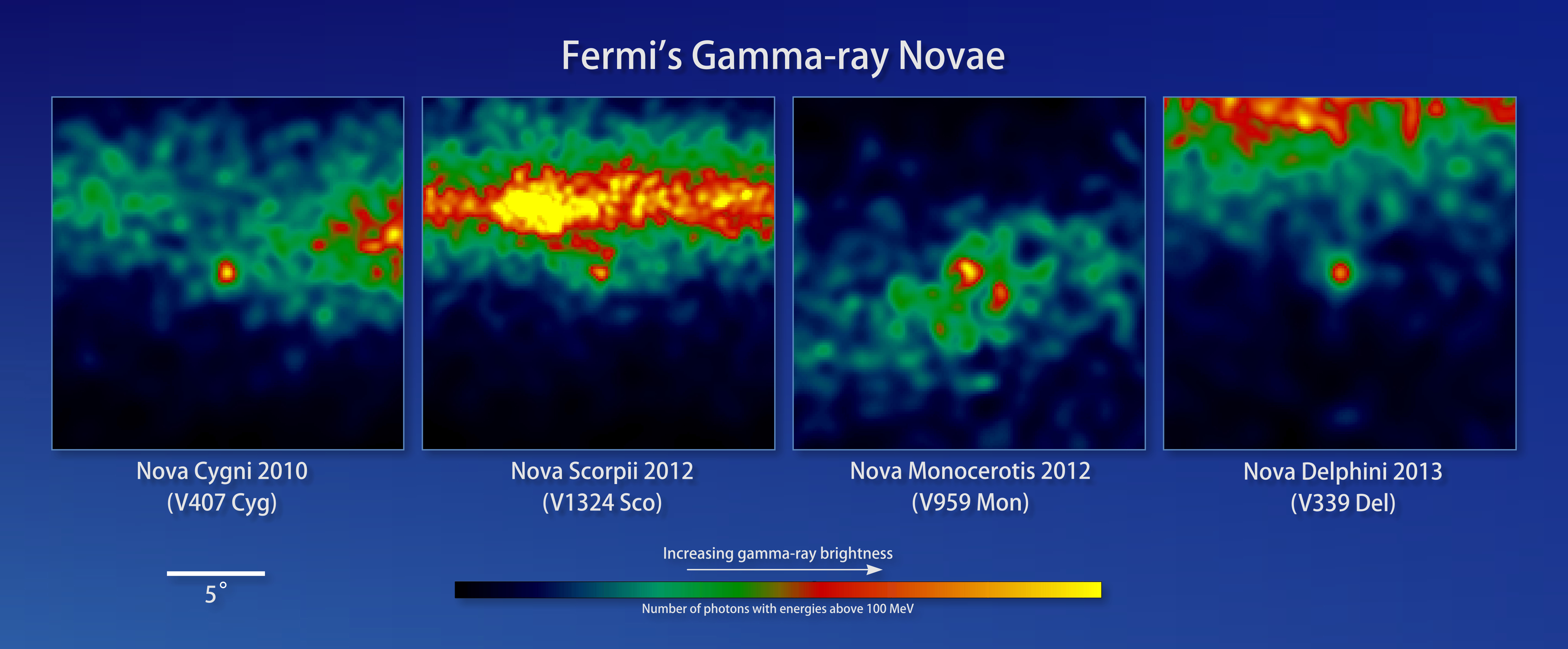
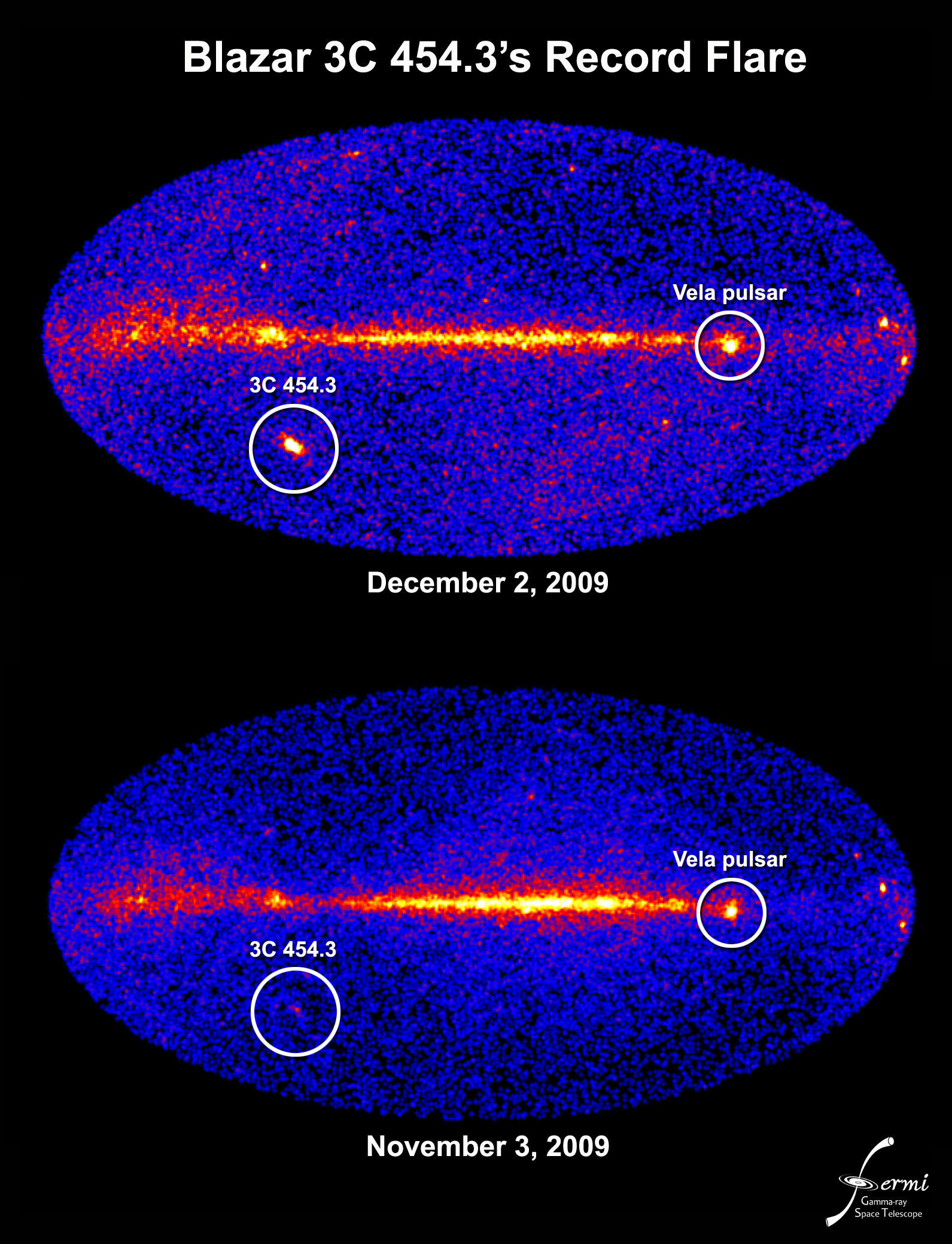
It’s a relatively straightforward picture — as far as complex astrophysics goes. But new observations with NASA’s Fermi Gamma-ray Space Telescope unexpectedly show that three classical novae — V959 Monocerotis 2012, V1324 Scorpii 2012, and V339 Delphini 2013 — and one rare nova, also produce gamma rays, the most energetic form of light.

“There’s a saying that one is a fluke, two is a coincidence, and three is a class, and we’re now at four novae and counting with Fermi,” said lead author Teddy Cheung from the Naval Research Laboratory in a press release.

The first nova detected in gamma rays was V407 Cygni — a rare star system in which a white dwarf interacts with a red giant — in March 2010.

One explanation for the gamma-ray emission is that the blast from the nova hits the hefty wind from the red giant, creating a shock wave that accelerates any charged particles to near the speed of light. These rapid particles, in turn, produce gamma rays.

But the gamma-ray peak follows the optical peak by a couple of days. This likely happens because the material the white dwarf ejects initially blocks the high-energy photons from escaping. So the gamma rays cannot escape until the material expands and thins.

But the later three novae are from systems that don’t have red giants and therefore their winds. There’s nothing for the blast wave to crash into.

“We initially thought of V407 Cygni as a special case because the red giant’s atmosphere is essentially leaking into space, producing a gaseous environment that interacts with the explosion’s blast wave,” said coauthor Steven Shore from the University of Pisa. “But this can’t explain more recent Fermi detections because none of those systems possess red giants.”

In a more typical system it’s likely that the blast creates multiple shock waves that expand into space at slightly different speeds. Faster shocks could blast into slower ones, creating the interaction necessary to produce gamma rays. Although, the team remains unsure if this is the case.

Astronomers estimate that between 20 and 50 novae occur each year in the Milky Way galaxy. Most go undetected, their visible light obscured by intervening dust, and their gamma rays dimmed by distance. Hopefully, future observations of nearby novae will shed light on the mysterious process producing gamma rays.

The results will appear in Science on August 1.

Posted on by Elizabeth Howell

Home Computers Discover Gamma-Ray Pulsars

Gamma-ray pulsars in the Milky Way's plane, found by volunteers using Einstein@Home. The sky map is from Fermi's Large Area Telescope. The brighter the color you see, the more intense the radiation in that spot. The small flags show the nationality of the volunteers whose computers spotted the pulsars. Credit: Knispel/Pletsch/AEI/NASA/DOE/Fermi LAT Collaboration

Imagine that you’re innocently running your computer in pursuit of helping data crunch a huge science project. Then, out of the thousands of machines running the project, yours happens to stumble across a discovery. That’s what happened to several volunteers with Einstein@Home, which seeks pulsars in data from the Fermi Gamma-Ray Space Telescope, among other projects.

“At first I was a bit dumbfounded and thought someone was playing a hoax on me. But after I did some research,” everything checked out. That someone as insignificant as myself could make a difference was amazing,” stated Kentucky resident Thomas M. Jackson, who contributed to the project.

Pulsars, a type of neutron star, are the leftovers of stars that exploded as supernovae. They rotate rapidly, with such precision in their rotation periods that they have sometimes been likened to celestial clocks. Although the discovery is exciting to the eight volunteers because they are the first to find these gamma-ray pulsars as part of a volunteer computing project, the pulsars also have some interesting scientific features.

Artist's illustration of a neutron star, a tiny remnant that remains after its predecessor star explodes. Here, the 12-mile (20-kilometer) sphere is compared with the size of Hannover, Germany. Credit: NASA's Goddard Space Flight Center
Artist’s illustration of a neutron star, a tiny remnant that remains after its predecessor star explodes. Here, the 12-mile (20-kilometer) sphere is compared with the size of Hannover, Germany. Credit: NASA’s Goddard Space Flight Center

The four pulsars were discovered in the plane of the Milky Way in an area that radio telescopes had looked at previously, but weren’t able to find themselves. This means that the pulsars are likely only visible in gamma rays, at least from the vantage point of Earth; the objects emit their radiation in a narrow direction with radio, but a wider stripe with gamma rays. (After the discoveries, astronomers used the Max Planck Institute for Radio Astronomy’s 100-meter Effelsberg radio telescope and the Australian Parkes Observatory to peer at those spots in the sky, and still saw no radio signals.)

Two of the pulsars also “hiccup” or exhibit a pulsar glitch, when the rotation sped up and then fell back to the usual rotation period a few weeks later. Astronomers are still learning more about these glitches, but they do know that most of them happen in young pulsars. All four pulsars are likely between 30,000 and 60,000 years old.

Artist's conception of a gamma-ray pulsar. Gamma rays are shown in purple, and radio radiation in green. Credit: NASA/Fermi/Cruz de Wilde
Artist’s conception of a gamma-ray pulsar. Gamma rays are shown in purple, and radio radiation in green. Credit: NASA/Fermi/Cruz de Wilde

“The first-time discovery of gamma-ray pulsars by Einstein@Home is a milestone – not only for us but also for our project volunteers. It shows that everyone with a computer can contribute to cutting-edge science and make astronomical discoveries,” stated co-author Bruce Allen, principal investigator of Einstein@Home. “I’m hoping that our enthusiasm will inspire more people to help us with making further discoveries.”

Einstein@Home is run jointly by the Center for Gravitation and Cosmology at the University of Wisconsin–Milwaukee and the Albert Einstein Institute in Hannover, Germany. It is funded by the National Science Foundation and the Max Planck Society. As for the volunteers, their names were mentioned in the scientific literature and they also received certificates of discovery for their work.

Source: Max Planck Institute for Gravitational Physics

Posted on by Nancy Atkinson

How the Fermi Spacecraft Almost Got Taken Out by a Relic of the Cold War

Artist concept of the Fermi Space Telescope. Credit: NASA.

As a space telescope scientist or satellite operator, the last thing you want to hear is that your expensive and possibly one-of-a kind — maybe irreplaceable — spacecraft is in danger of colliding with a piece of space junk. On March 29, 2012, scientists from the Fermi Gamma-ray Space Telescope were notified that their spacecraft was at risk from a collision. And the object heading towards the Fermi spacecraft at a relative speed of 44,000 km/h (27,000 mph) wasn’t just a fleck of paint or tiny bolt.

Fermi was facing a possible direct hit by a 1,400 kg (3,100-pound) defunct Russian spy satellite dating back to the Cold War, named Cosmos 1805. If the two satellites met in orbit, the collision would release as much energy as two and a half tons of high explosives, destroying both spacecraft and creating more pieces of space junk in the process.

But this story has a happy ending, with the Fermi telescope still operating and continuing its mission to map the highest-energy light in the universe, all thanks to a little orbital traffic control.

You can watch the video here for the complete story, or read more at the Fermi website about how the Fermi Space Telescope dodged a speeding bullet.

Posted on by Nancy Atkinson

Cosmic Rays and Exploding Stars

Cosmic Rays
Artists impression of cosmic rays. Credit: NASA

Scientists have known about cosmic rays for a century. But these high-energy subatomic particles, which stream through space at nearly the speed of light and crash into the Earth’s upper atmosphere, have been mostly a mystery. The primary reason: researchers have been unable to tell where they come from, or how they’re born. But new research has shed new light on the origins of cosmic rays: supernovae. (Read our article about this discovery).

Today, Thursday, Feb. 28,at 20:00-20:30 UTC (12:00-12:30 p.m. PST, 3:00 pm EST) Dr. Stefan Funk of the Kavli Institute for Particle Astrophysics and Cosmology (KIPAC) will answer questions from the web. He led the research team that was able to track gamma rays — the most energetic form of electromagnetic radiation, or light — back to the remnants of supernova explosions, using the Fermi Gamma Ray Telescope. The finding offers the first astrophysical evidence for how cosmic rays are produced, as well as where they are generated: in the shock waves that emanate from an exploded star.
Continue reading “Cosmic Rays and Exploding Stars”

Posted on by Nancy Atkinson

Fermi Measures Light from All the Stars That Have Ever Existed

This plot shows the locations of 150 blazars (green dots) used in the a new by the Fermi Gamma-Ray Telescope. Credit: NASA/DOE/Fermi LAT Collaboration

All the light that has been produced by every star that has ever existed is still out there, but “seeing” it and measuring it precisely is extremely difficult. Now, astronomers using data from NASA’s Fermi Gamma-ray Space Telescope were able to look at distant blazars to help measure the background light from all the stars that are shining now and ever were. This enabled the most accurate measurement of starlight throughout the universe, which in turn helps establish limits on the total number of stars that have ever shone.

“The optical and ultraviolet light from stars continues to travel throughout the universe even after the stars cease to shine, and this creates a fossil radiation field we can explore using gamma rays from distant sources,” said lead scientist Marco Ajello from the Kavli Institute for Particle Astrophysics and Cosmology at Stanford University in California and the Space Sciences Laboratory at the University of California at Berkeley.

Their results also provide a stellar density in the cosmos of about 1.4 stars per 100 billion cubic light-years, which means the average distance between stars in the universe is about 4,150 light-years.

The total sum of starlight in the cosmos is called the extragalactic background light (EBL), and Ajello and his team investigated the EBL by studying gamma rays from 150 blazars, which are among the most energetic phenomena in the universe. They are galaxies powered by extremely energetic black holes: they have energies greater than 3 billion electron volts (GeV), or more than a billion times the energy of visible light.

The astronomers used four years of Fermi data on gamma rays with energies above 10 billion electron volts (GeV), and the Fermi Large Area Telescope (LAT) instrument is the first to detect more than 500 sources in this energy range.

To gamma rays, the EBL functions as a kind of cosmic fog, but Fermi measured the amount of gamma-ray absorption in blazar spectra produced by ultraviolet and visible starlight at three different epochs in the history of the universe.

Fermi measured the amount of gamma-ray absorption in blazar spectra produced by ultraviolet and visible starlight at three different epochs in the history of the universe. (Credit: NASA’s Goddard Space Flight Center)

“With more than a thousand detected so far, blazars are the most common sources detected by Fermi, but gamma rays at these energies are few and far between, which is why it took four years of data to make this analysis,” said team member Justin Finke, an astrophysicist at the Naval Research Laboratory in Washington.

Gamma rays produced in blazar jets travel across billions of light-years to Earth. During their journey, the gamma rays pass through an increasing fog of visible and ultraviolet light emitted by stars that formed throughout the history of the universe.

Occasionally, a gamma ray collides with starlight and transforms into a pair of particles — an electron and its antimatter counterpart, a positron. Once this occurs, the gamma ray light is lost. In effect, the process dampens the gamma ray signal in much the same way as fog dims a distant lighthouse.

From studies of nearby blazars, scientists have determined how many gamma rays should be emitted at different energies. More distant blazars show fewer gamma rays at higher energies — especially above 25 GeV — thanks to absorption by the cosmic fog.

The researchers then determined the average gamma-ray attenuation across three distance ranges: The closest group was from when the universe was 11.2 years old, a middle group of when the Universe was 8.6 billion years old, and the farthest group from when the Universe was 4.1 billion years old.

This animation tracks several gamma rays through space and time, from their emission in the jet of a distant blazar to their arrival in Fermi’s Large Area Telescope (LAT). During their journey, the number of randomly moving ultraviolet and optical photons (blue) increases as more and more stars are born in the universe. Eventually, one of the gamma rays encounters a photon of starlight and the gamma ray transforms into an electron and a positron. The remaining gamma-ray photons arrive at Fermi, interact with tungsten plates in the LAT, and produce the electrons and positrons whose paths through the detector allows astronomers to backtrack the gamma rays to their source.

From this measurement, the scientists were able to estimate the fog’s thickness.

“These results give you both an upper and lower limit on the amount of light in the Universe and the amount of stars that have formed,” said Finke during a press briefing today. “Previous estimates have only been an upper limit.”

And the upper and lower limits are very close to each other, said Volker Bromm, an astronomer at the University of Texas, Austin, who commented on the findings. “The Fermi result opens up the exciting possibility of constraining the earliest period of cosmic star formation, thus setting the stage for NASA’s James Webb Space Telescope,” he said. “In simple terms, Fermi is providing us with a shadow image of the first stars, whereas Webb will directly detect them.”

Measuring the extragalactic background light was one of the primary mission goals for Fermi, and Ajello said the findings are crucial for helping to answer a number of big questions in cosmology.

A paper describing the findings was published Thursday on Science Express.

Source: NASA

Posted on by Nancy Atkinson

Ghostly Jets Haunt the Milky Way’s Black Hole

This artist's conception shows an edge-on view of the Milky Way galaxy and newly discovered gamma-ray jets extending from the central black hole. Credit: David A. Aguilar (CfA)

[/caption]

A ghost is haunting the Milky Way’s central black hole, revealing the galactic nucleus was likely much more active in the past than it is now. Scientists using the Fermi space telescope have found faint apparitions of what must have been powerful gamma-ray jets emanating from our galaxy’s center.

“These faint jets are a ghost or after-image of what existed a million years ago,” said Meng Su, an astronomer at the Harvard-Smithsonian Center for Astrophysics (CfA), and lead author of a new paper in the Astrophysical Journal. “They strengthen the case for an active galactic nucleus in the Milky Way’s relatively recent past.”

This is the first time this type of jet has been detected from the Milky Way’s black hole. Scientists know that other active galaxies have cores that glow brightly, powered by supermassive black holes swallowing material, and often spit twin jets in opposite directions.

The two beams, or jets found by Fermi observations extend from the galactic center to a distance of 27,000 light-years above and below the galactic plane.
The newfound jets may be related to mysterious gamma-ray bubbles that Fermi detected in 2010. Those bubbles also stretch 27,000 light-years from the center of the Milky Way. However, where the bubbles are perpendicular to the galactic plane, the gamma-ray jets are tilted at an angle of 15 degrees. This may reflect a tilt of the accretion disk surrounding the supermassive black hole.

“The central accretion disk can warp as it spirals in toward the black hole, under the influence of the black hole’s spin,” explained co-author Douglas Finkbeiner of the CfA. “The magnetic field embedded in the disk therefore accelerates the jet material along the spin axis of the black hole, which may not be aligned with the Milky Way.”

The two structures also formed differently. The jets were produced when plasma squirted out from the galactic center, following a corkscrew-like magnetic field that kept it tightly focused. The gamma-ray bubbles likely were created by a “wind” of hot matter blowing outward from the black hole’s accretion disk. As a result, they are much broader than the narrow jets.

Both the jets and bubbles are powered by inverse Compton scattering. In that process, electrons moving near the speed of light collide with low-energy light, such as radio or infrared photons. The collision increases the energy of the photons into the gamma-ray part of the electromagnetic spectrum.

The discovery leaves open the question of when the Milky Way was last active. A minimum age can be calculated by dividing the jet’s 27,000-light-year length by its approximate speed. However, it may have persisted for much longer.

“These jets probably flickered on and off as the supermassive black hole alternately gulped and sipped material,” said Finkbeiner.

It would take a tremendous influx of matter for the galactic core to fire up again. Finkbeiner estimates that a molecular cloud weighing about 10,000 times as much as the Sun would be required.

“Shoving 10,000 suns into the black hole at once would do the trick. Black holes are messy eaters, so some of that material would spew out and power the jets,” he said.

Source: CfA

Posted on by Ray Sanders

A Psychedelic Guide to Tycho’s Supernova Remnant

Gamma-rays detected by Fermi's LAT show that the remnant of Tycho's supernova shines in the highest-energy form of light. This portrait of the shattered star includes gamma rays (magenta), X-rays (yellow, green, and blue), infrared (red) and optical data. Image Credit: Gamma ray, NASA/DOE/Fermi LAT Collaboration; X-ray, NASA/CXC/SAO; Infrared, NASA/JPL-Caltech; Optical, MPIA, Calar Alto, O. Krause et al. and DSS)

[/caption]

By no means are we suggesting that NASA’s Fermi Gamma-Ray Space Telescope can induce altered states of awareness, but this ‘far-out’ image is akin to 1960’s era psychedelic art. However, the data depicted here provides a new and enlightened way of looking at an object that’s been observed for over 400 years. After years of study, data collected by Fermi has revealed Tycho’s Supernova Remnant shines brightly in high-energy gamma rays.

The discovery provides researchers with additional information on the origin of cosmic rays (subatomic particles that are on speed). The exact process that gives cosmic rays their energy isn’t well understood since charged particles are easily deflected by interstellar magnetic fields. The deflection by interstellar magnetic fields makes it impossible for researchers to track cosmic rays to their original sources.

“Fortunately, high-energy gamma rays are produced when cosmic rays strike interstellar gas and starlight. These gamma rays come to Fermi straight from their sources,” said Francesco Giordano at the University of Bari in Italy.

But here’s some not-so-psychedelic facts about supernova remnants in general and Tycho’s in particular:

When a massive star reaches the end of its lifetime, it can explode, leaving behind a supernova remnant consisting of an expanding shell of hot gas propelled by the blast shockwave. In many cases, a supernova explosion can be visible on Earth – even in broad daylight. In November of 1572, a new “star” was discovered in the constellation Cassiopeia. The discovery is now known to be the most visible supernova in the past 400 years. Often called “Tycho’s supernova”, the remnant shown above is named after Danish astronomer Tycho Brahe, who spent a great deal of time studying the supernova.

Tycho's map shows the supernova's position (largest symbol, at top) relative to the stars that form Cassiopeia. Image credit: University of Toronto
The 1572 supernova event occurred when the night sky was considered to be a fixed and unchanging part of the universe. Tycho’s account of the discovery gives a sense of just how profound his discovery was. Regarding his discovery, Tycho stated, “When I had satisfied myself that no star of that kind had ever shone forth before, I was led into such perplexity by the unbelievability of the thing that I began to doubt the faith of my own eyes, and so, turning to the servants who were accompanying me, I asked them whether they too could see a certain extremely bright star…. They immediately replied with one voice that they saw it completely and that it was extremely bright”

In 1949, physicist Enrico Fermi (the namesake for the Fermi Gamma-ray Space Telescope) theorized that high-energy cosmic rays were accelerated in the magnetic fields of interstellar gas clouds. Following up on Fermi’s work, astronomers learned that supernova remnants might be the best candidate sites for magnetic fields of such magnitude.

One of the main goals of the Fermi Gamma-ray Space Telescope is to better understand the origins of cosmic rays. Fermi’s Large Area Telescope (LAT) can survey the entire sky every three hours, which allows the instrument to build a deeper view of the gamma-ray sky. Since gamma rays are the most energetic form of light, studying gamma ray concentrations can help researchers detect the particle acceleration responsible for cosmic rays.

Co-author Stefan Funk (Kavli Institute for Particle Astrophysics and Cosmology) adds, “This detection gives us another piece of evidence supporting the notion that supernova remnants can accelerate cosmic rays.”

After scanning the sky for nearly three years, Fermi’s LAT data showed a region of gamma-ray emissions associated with the remnant of Tycho’s supernova. Keith Bechtol, (KIPAC graduate student) commented on the discovery, saying, “We knew that Tycho’s supernova remnant could be an important find for Fermi because this object has been so extensively studied in other parts of the electromagnetic spectrum. We thought it might be one of our best opportunities to identify a spectral signature indicating the presence of cosmic-ray protons”

The team’s model is based on LAT data, gamma-rays mapped by ground-based observatories and X-ray data. The conclusion the team has come to regarding their model is that a process called pion production is the best explanation for the emissions. The animation below depicts a proton moving at nearly the speed of light and striking a slower-moving proton. The protons survive the collision, but their interaction creates an unstable particle — a pion — with only 14 percent of the proton’s mass. In 10 millionths of a billionth of a second, the pion decays into a pair of gamma-ray photons.

If the team’s interpretation of the data is accurate, then within the remnant, protons are being accelerated to near the speed of light. After being accelerated to such tremendous speeds, the protons interact with slower particles and produce gamma rays. With all the amazing processes at work in the remnant of Tycho’s supernova, one could easily imagine how impressed Brahe would be.

And no tripping necessary.

Learn more about the Fermi Gamma-ray Space Telescope at: http://www.nasa.gov/mission_pages/GLAST/main/index.html

Source: Fermi Gamma-ray Space Telescope Mission News

Posted on by Nancy Atkinson

Astronomers Find the Justin Bieber of Millisecond Pulsars

This cluster is 27,000 light-years away and lies farther than the center of our galaxy in the constellation Sagittarius. Credit: NASA/ESA/I. King, Univ. of Calif., Berkeley/Wikisky.org

[/caption]

Astronomers using the Fermi Gamma-ray Space Telescope have found a surprisingly young, powerful and luminous millisecond pulsar. Over the past three years, Fermi has detected more than 100 gamma-ray pulsars and typically the ages of these objects are at least a billion year old. But this new object is just a youngster, born only about 25 million years ago.

“It is a bit like finding Justin Bieber when you thought you were at a Rolling Stones concert,” said Victoria Kaspi, physics professor, McGill University in Montreal, during a teleconference about two new discoveries made with the Fermi telescope. “Fermi has represented a huge leap forward in finding things that couldn’t have been imagined 25 years ago.”

In addition to the very young and bright pulsar, researchers announced they have also discovered a set of nine previously unknown gamma-ray pulsars, a new type that have extremely low luminosity. These were uncovered with a new technique to more efficiently sift through Fermi data.

The young millisecond pulsar, named PSR J1823?3021A was found within the globular cluster NGC 6624, not far from the center of our galaxy. Fermi has detected pulsars in globular clusters before, but usually what it finds are the combined gamma rays from many ancient pulsars within the clusters. But this time, surprisingly, the gamma rays originated from just one very powerful millisecond pulsar.

“At first we thought it was perhaps one hundred millisecond pulsars, but now we see it is just one,” said Paulo Freire, from the Max Planck Institute for Radio Astronomy in Bonn, Germany, also speaking to reporters during the teleconference. Freire is the lead author on a new paper published in the Astrophysical Journal. “It must have formed recently based on how rapidly it’s emitting energy. It’s a bit like finding a screaming baby in a quiet retirement home. This was a rather surprising discovery for everyone involved.”

A pulsar is a type of neutron star that emits electromagnetic energy at periodic intervals, sending out signals almost like a lighthouse. Pulsars that combine incredible density with extreme rotation are called millisecond pulsars. These millisecond pulsars are especially fascinating, as they are city-sized spheres about half millions times Earth’s mass, spinning at up to 43,000 revolutions per minute.

Millisecond pulsars are thought to achieve such speeds because they are gravitationally bound in binary systems with normal stars. During part of their stellar lives, gas flows from the normal star to the pulsar. Over time, the impact of this falling gas gradually spins up the pulsar’s rotation.

This plot shows the positions of nine new pulsars (magenta) discovered by Fermi and of an unusual millisecond pulsar (green) that Fermi data reveal to be the youngest such object known. With this new batch of discoveries, Fermi has detected more than 100 pulsars in gamma rays. Credit: AEI and NASA/DOE/Fermi LAT Collaboration

The nine new low luminosity pulsars found with Fermi emit less gamma radiation than those previously known and rotate only between three and twelve times per second. Only one of these pulsars was later also found to emit radio waves. Without the new technique, astronomers wouldn’t have found this faint pulsars.

““We used a new kind of hierarchical algorithm which we had originally developed for the search for gravitational waves, and we were quickly rewarded,” said Bruce Allen, director of the Max Planck Institute for Gravitational Physics, a co-author on the recent discoveries.

Using what is called a blind search, computers check many different combinations of position and rotational behavior, to see if they match the arrival times of photons hitting the Fermi Large Area Telescope (LAT) coming from the same direction. The search used the 8,000 photons deemed most probable to come from a pulsar at the recognized position, which Fermi’s LAT had collected during its three years in orbit. When the photon arrival times match up with the putative pulsar position and rotation model, a regular pattern of peaks appears in the gamma-ray photon counts, as a function of the rotational position of the pulsar, and a new gamma-ray pulsar has been discovered.

“It is a little like sifting through a pile of sand looking for diamonds,” Allen said, adding that the search is ongoing and they hope to find more.

Additionally, Allen said, users of the Einstein@Home project can now be part of this search, to help specifically to search for the first pure gamma-ray millisecond-pulsar. Allen is the director of this project and said this discovery would be a significant contribution to our understanding of pulsars.

NASA has a new interactive web feature about Fermi and the 100 pulsars it has now found.

Sources: Max Planck Institute, NASA, More info, images and vidoes at this NASA page

Posted on by Nicholos Wethington

Fermi Spies Energetic Blazar Flare

A comparison of the Fermi images from November 2nd and December 3rd of this year, showing the brightening of 3C 454.3. Image Credit: NASA

[/caption]

The blazar 3C 454.3, a bright source of gamma rays from a galaxy 7 billion light-years away just got a whole lot brighter. Observations from the Fermi gamma-ray telescope confirm that since September 15th the blazar has flared up considerably, increasing in gamma-ray brightness by about ten times in the from earlier this past summer, making it currently the brightest gamma-ray source in the sky.

3C 454.3 is a blazar, a jet of energetic particles that is caused by the supermassive black hole at the center of a galaxy. Most galaxies are thought to house a supermassive black hole at their center, and as it chomps down matter from the accretion disk that surrounds it, the supermassive black hole can form large jets that stream out light and energy in fantastic proportions. In the case of 3C 454.3, one of these jets is aimed at the Earth, which allows for us to see and study it.

This blazar has started to outshine the Vela pulsar, which because it is only 1,000 light-years away from the Earth is generally the brightest gamma-ray source in the sky. 3C 454.3 is almost twice as bright as Vela in the gamma-ray part of the spectrum, even though it lies 7 million times further away from the Earth. 3c 454.3 has also brightened significantly in the infrared, X-ray, radio and visible light.

This is not the first time the blazar has shown an increase in brightness. Over the course of observations of the blazar, it flared-up in brightness in May 2005, and again in July and August of 2007.

Dr. Erin Wells Bonning, Postdoctoral Associate at the Yale Center for Astronomy and Astrophysics, said of the recent flare in comparison with previous brightening events:

“In 2005, it reached a R-band magnitude of 12. Our peak observed R-band magnitude was 13.83, so we’re still not at the brightness of the 2005 outburst (about a factor of 5 below). On July 19, 2007, it reached a R-band magnitude of 13, not as bright as the 2005 event, but still brighter than we see it now. In 2005, there were no gamma-ray instruments to observe 3C 454.3, but the 2007 flare was observed by AGILE with a flux above 100 MeV of 3 +- 1 * 10^-6 cts/s/cm^s. The Fermi and AGILE count rates for Dec 2-3, 2009  are 6-9 times as high. So, interestingly, although it is not currently as bright optically as it was in 2007, it is a good deal brighter in gamma-rays.”

The Fermi gamma-ray space telescope (formerly GLAST) keeps tabs on the gamma-ray emissions from many sources in the sky. 3C 454.3 is just one of the top ten brightest sources of gamma-rays visible to the satellite, a list of which can be found in an article Nancy wrote in March, The Top Ten Gamma-Ray Sources from the Fermi Telescope.

Of course, the blazar 3C 454.3 is not as intrinsically bright as many of the Gamma-Ray Bursts observed by telescopes like Swift and Fermi, but it is the consistently brightest source of gamma-rays in the sky right now. Bonning said that, “While both GRBs and blazars are highly beamed toward us, the Lorentz factors (speed of particles in the jet) associated with GRBs are much higher than in blazars, causing them to appear brighter due to special relativistic effects.”

Observations 3C 454.3 are continuing in all wavelengths to capture the light curve of the event, and better understand these periodic flares. Bonning said, “The source has been relatively quiescent since it emerged from behind the Sun, and began to increase in brightness around the end of July. It then entered a bright period of fairly rapid variability, peaking every 20 days or so. The most recent, very intense, flare began around the end of November. Per our [Astronomer’s Telegram], since Nov 21, 3C 454 has increased about a factor of 3 in brightness in both optical and infrared. (B, V, and R filters are in optical wavelengths, and J and K are near-infrared).  Similarly, the gamma-ray flux has increased also by a factor of 3 in the 0.1-300 GeV band over the same period.”

The cause of the intermittent flare-ups in 3C 454.3 and other blazars is still a mystery, but this current brightening will give astronomers better data as to what the possible cause could be. There seem to be no periodic events associated with the flares in blazars (with the exception of the possible “supermassive black hole binary” OJ 287).

Bonning said of a potential cause, “This is actually a very active field of research – there are numerous existing models, but no one hypothesis is clearly preferred. Perhaps particles have been shocked at some location in the blazar jet, or the jet may be precessing so that is closer to our line of sight, or there may be some other explanation.”

There will be numerous telescopes around the world zooming in on the current flare-up. According to Bonning:

“Blazars are multi-wavelength objects — their spectral energy distribution covers radio through gamma-rays, so a diverse collection of facilities will be observing 3C 454.3 during this outburst. Besides Fermi, the Italian AGILE satellite has been observing in gamma rays. The Swift X-ray telescope began monitoring in early December.  The blazar monitoring group at Boston University headed by Alan Marscher is observing it with VLBA (radio; 13GHz). There is also a radio astronomy group at Michigan also observing with VLBA, as well one headed by Yuri Kovalev at Max Planck institute in Germany.  There is an optical program with the ATOM telescope associated with the HESS TeV instrument in Namibia. (3C 454.3 is not bright at TeV energies, by the way.)  This is not an exhaustive list by any means, but at any rate numerous facilities across the globe and operating at a wide range of energies will be taking a very close look at 3C 454.3 as it goes through this flare.”

Source: NASA press release, email interview with Erin Wells Bonning

Posted on by Nancy Atkinson

Fermi Finds Gamma-Ray Microquasar

Fermi’s Large Area Telescope has detected bursts of gamma-rays in the binary system Cygnus X-3, which astronomers say are coming from a microquasar. While microquasars have strong emissions across is a broad range of wavelengths, this is the first time this type of object has been detected in gamma rays. “Cygnus X-3 is a genuine microquasar and it’s the first for which we can prove high-energy gamma-ray emission,” said Stéphane Corbel at Paris Diderot University in France.

n Cygnus X-3, an accretion disk surrounding a black hole or neutron star orbits close to a hot, massive star. Gamma rays (purple, in this illustration) likely arise when fast-moving electrons above and below the disk collide with the star's ultraviolet light. Fermi sees more of this emission when the disk is on the far side of its orbit. Credit: NASA's Goddard Space Flight Center
n Cygnus X-3, an accretion disk surrounding a black hole or neutron star orbits close to a hot, massive star. Gamma rays (purple, in this illustration) likely arise when fast-moving electrons above and below the disk collide with the star's ultraviolet light. Fermi sees more of this emission when the disk is on the far side of its orbit. Credit: NASA's Goddard Space Flight Center

Microquasars are stellar mass object that displays in miniature some of the properties of quasars: a normal star begins shedding its matter onto either a neutron star or a black hole. This phenomenon produces large amounts of radiation and “jets” of material moving at relativistic speeds—more than 10% the speed of light—away from the star. These “relativistic jets” are a great mystery that astronomers are still trying to understand, but this new gamma-ray microquasar could provide new ways to study them.

At the center of Cygnus X-3 lies a massive Wolf-Rayet star. With a surface temperature of 100,255.372 Kelvin (180,000 degrees F,) or about 17 times hotter than the sun, the star is so hot that its mass bleeds into space in the form of a powerful outflow called a stellar wind. “In just 100,000 years, this fast, dense wind removes as much mass from the Wolf-Rayet star as our sun contains,” said Robin Corbet at the University of Maryland, Baltimore County.

The researchers matched the gamma-rays to the known orbital period of the Cygnus X-3 microquasar in order to confirm that the strong pulses of radiation were, in fact, originating from the object. They also matched the gamma-rays with radio emission from the relativistic jets of Cygnus X-3.

Brighter colors indicate greater numbers of gamma rays detected in this Fermi LAT view of a region centered on the position of Cygnus X-3 (circled). The brightest sources are pulsars. Credit: NASA/DOE/Fermi LAT Collaboration
Brighter colors indicate greater numbers of gamma rays detected in this Fermi LAT view of a region centered on the position of Cygnus X-3 (circled). The brightest sources are pulsars. Credit: NASA/DOE/Fermi LAT Collaboration

Every 4.8 hours, a compact companion embedded in a disk of hot gas wheels around the star. “This object is most likely a black hole, but we can’t yet rule out a neutron star,” Corbet said.

Between Oct. 11 and Dec. 20, 2008, and again between June 8 and Aug. 2, 2009, Cygnus X-3 was unusually active. The team found that outbursts in the system’s gamma-ray emission preceded flaring in the radio jet by roughly five days, strongly suggesting a relationship between the two.

These new findings should provide more information about the formation of such mysterious and fast-moving relativistic jets. This research appears in the 26 November issue of Science Express.

Read the team’s abstract

Sources: Science, Goddard Spaceflight Center