Artist view of an active supermassive black hole. Credit: ESO/L. Calçada
In the classical theory of general relativity, black holes are relatively simple objects. They can be described by just three properties: mass, charge, and rotation. But we know that general relativity is an incomplete theory. Quantum mechanics is most apparent in the behavior of tiny objects, but it also plays a role in large objects such as black holes. To describe black holes at a quantum level, we need a theory of quantum gravity. We don’t have a complete theory yet, but what know so far is that quantum mechanics makes black holes more complex, giving them properties such as temperature and perhaps even pressure.
A black hole is the final form a massive star collapses to. The light (and spacetime itself) is warped around the black hole's event horizon due to extreme gravitational effects. This is as accurate as we can be to visualizing an actual black hole as it was generated with a code that implemented General Relativity accurately. Credit and Copyright: Paramount Pictures/Warner Bros.
Mathematical Model used to create the image developed by Dr. Kip Thorne
A neutron star is perhaps one of the most awe-inspiring and mysterious things in the Universe. Composed almost entirely of neutrons with no net electrical charge, they are the final phase in the life-cycle of a giant star, born of the fiery explosions known as supernovae. They are also the densest known objects in the universe, a fact which often results in them becoming a black hole if they undergo a change in mass.
For some time, astronomers have been confounded by this process, never knowing where or when a neutron star might make this final transformation. But thanks to a recent study by a team of researchers from Goethe University in Frankfurt, Germany, it may now be possible to determine the absolute maximum mass that is required for a neutron star to collapse, giving birth to a new black hole.
Have you ever been doing thermodynamics in a closed system and noticed that there’s a finite number of ways that things can be arranged, and they tend towards disorder? Of course you have, we all have. That’s entropy. And here in our Universe, entropy is on the rise. Let’s learn about entropy in its specific, thermodynamic ways, and then figure out what this means for the future of the Universe. Continue reading “Astronomy Cast Ep. 391: Entropy”
A historical reconstruction of what Robert Hooke looked like. Credit: Wikipedia/Rita Greer/FAL
The spring is a marvel of human engineering and creativity. For one, it comes in so many varieties – the compression spring, the extension spring, the torsion spring, the coil spring, etc. – all of which serve different and specific functions. These functions in turn allow for the creation of many man-made objects, most of which emerged as part of the Scientific Revolution during the late 17th and 18th centuries.
As an elastic object used to store mechanical energy, the applications for them are extensive, making possible such things as an automotive suspension systems, pendulum clocks, hand sheers, wind-up toys, watches, rat traps, digital micromirror devices, and of course, the Slinky.
Like so many other devices invented over the centuries, a basic understanding of the mechanics is required before it can so widely used. In terms of springs, this means understanding the laws of elasticity, torsion and force that come into play – which together are known as Hooke’s Law.
Hooke’s Law is a principle of physics that states that the that the force needed to extend or compress a spring by some distance is proportional to that distance. The law is named after 17th century British physicist Robert Hooke, who sought to demonstrate the relationship between the forces applied to a spring and its elasticity.
Illustration of Hooke’s Law, showing the relationship between force and distance when applied to a spring. Credit: GSU/hyperphysics
He first stated the law in 1660 as a Latin anagram, and then published the solution in 1678 as ut tensio, sic vis – which translated, means “as the extension, so the force” or “the extension is proportional to the force”).
This can be expressed mathematically as F= -kX, where F is the force applied to the spring (either in the form of strain or stress); X is the displacement of the spring, with a negative value demonstrating that the displacement of the spring once it is stretched; and k is the spring constant and details just how stiff it is.
Hooke’s law is the first classical example of an explanation of elasticity – which is the property of an object or material which causes it to be restored to its original shape after distortion. This ability to return to a normal shape after experiencing distortion can be referred to as a “restoring force”. Understood in terms of Hooke’s Law, this restoring force is generally proportional to the amount of “stretch” experienced.
In addition to governing the behavior of springs, Hooke’s Law also applies in many other situations where an elastic body is deformed. These can include anything from inflating a balloon and pulling on a rubber band to measuring the amount of wind force is needed to make a tall building bend and sway.
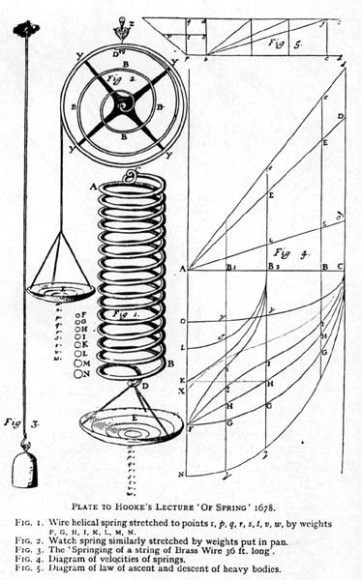
This law has had many important practical applications, with one being the creation of a balance wheel, which made possible the creation of the mechanical clock, the portable timepiece, the spring scale and the manometer (aka. the pressure gauge). Also, because it is a close approximation of all solid bodies (as long as the forces of deformation are small enough), numerous branches of science and engineering as also indebted to Hooke for coming up with this law. These include the disciplines of seismology, molecular mechanics and acoustics.
However, like most classical mechanics, Hooke’s Law only works within a limited frame of reference. Because no material can be compressed beyond a certain minimum size (or stretched beyond a maximum size) without some permanent deformation or change of state, it only applies so long as a limited amount of force or deformation is involved. In fact, many materials will noticeably deviate from Hooke’s law well before those elastic limits are reached.
Still, in its general form, Hooke’s Law is compatible with Newton’s laws of static equilibrium. Together, they make it possible to deduce the relationship between strain and stress for complex objects in terms of the intrinsic materials of the properties it is made of. For example, one can deduce that a homogeneous rod with uniform cross section will behave like a simple spring when stretched, with a stiffness (k) directly proportional to its cross-section area and inversely proportional to its length.
The balance wheel in a cheap 1950s alarm clock (the Apollo, by Lux Mfg. Co.) showing the balance wheel (1) and regulator (2). Credit: Wikipedia/Public Domain
Another interesting thing about Hooke’s law is that it is a a perfect example of the First Law of Thermodynamics. Any spring when compressed or extended almost perfectly conserves the energy applied to it. The only energy lost is due to natural friction.
In addition, Hooke’s law contains within it a wave-like periodic function. A spring released from a deformed position will return to its original position with proportional force repeatedly in a periodic function. The wavelength and frequency of the motion can also be observed and calculated.
The modern theory of elasticity is a generalized variation on Hooke’s law, which states that the strain/deformation of an elastic object or material is proportional to the stress applied to it. However, since general stresses and strains may have multiple independent components, the “proportionality factor” may no longer be just a single real number.
A good example of this would be when dealing with wind, where the stress applied varies in intensity and direction. In cases like these, it is best to employ a linear map (aka. a tensor) that can be represented by a matrix of real numbers instead of a single value.
If you enjoyed this article there are several others that you will enjoy on Universe Today. Here is one about Sir Isaac Newton’s contributions to the many fields of science. Here is an interesting article about gravity.
There are also some great resources online, such as this lecture on Hooke’s Law that you can watch on academicearth.org. There is also a great explanation of elasticity on howstuffworks.com.
After some time, this cold glass will reach thermal equilibrium
Perhaps there’s no better way to understand entropy than to grasp the second law of thermodynamics, and vice versa. This law states that the entropy of an isolated system that is not in equilibrium will increase as time progresses until equilibrium is finally achieved.
Let’s try to elaborate a little on this equilibrium thing. Note that in the succeeding examples, we’ll assume that they’re both isolated systems.
First example. Imagine putting a hot body and a cold body side by side. What happens after some time? That’s right. They both end up in the same temperature; one that is lower than the original temperature of the hotter one and higher than the original temperature of the colder one.
Second example. Ever heard of a low pressure area? It’s what weather reporters call a particular region that’s characterized by strong winds and perhaps some rain. This happens because all fluids flow from a region of high pressure to a region of low pressure. Thus, when the fluid, air in this case, comes rushing in, they do so in the form of strong winds. This goes on until the pressures in the adjacent regions even out.
In both cases, the physical quantities which started to be uneven between the two bodies/regions even out in the end, i.e., when equilibrium is achieved. The measurement of the extent of this evening-out process is called entropy.
During the process of attaining equilibrium, it is possible to tap into the system to perform work, as in a heat engine. Notice, however, that work can only be done for as long as there is a difference in temperature. Without it, like when maximum entropy has already been achieved, there is no way that work can be performed.
Since the concept of entropy applies to all isolated systems, it has been studied not only in physics but also in information theory, mathematics, as well as other branches of science and applied science.
Because the accepted view of the universe is that of one that is finite, then it can very well be considered as a closed system. As such, it should also be governed by the second law of thermodynamics. Thus, like in all isolated systems, the entropy of the universe is expected to be increasing.
So what? Well, also just like all isolated systems, the universe is therefore also expected to end up in a useless heap in equilibrium, a.k.a. a heat death, wherein energy can no longer be extracted from anymore. To give you some relief, not everyone involved in the study of cosmology is totally in agreement with entropy’s so-called role in the grand scheme of things though.
