Have you ever taken a look at a piece of firewood and said to yourself, “gee, I wonder how much energy it would take to split that thing apart”? Chances are, no you haven’t, few people do. But for physicists, asking how much energy is needed to separate something into its component pieces is actually a pretty important question.
In the field of physics, this is what is known as binding energy, or the amount of mechanical energy it would take to disassemble an atom into its separate parts. This concept is used by scientists on many different levels, which includes the atomic level, the nuclear level, and in astrophysics and chemistry.
Nuclear Force:
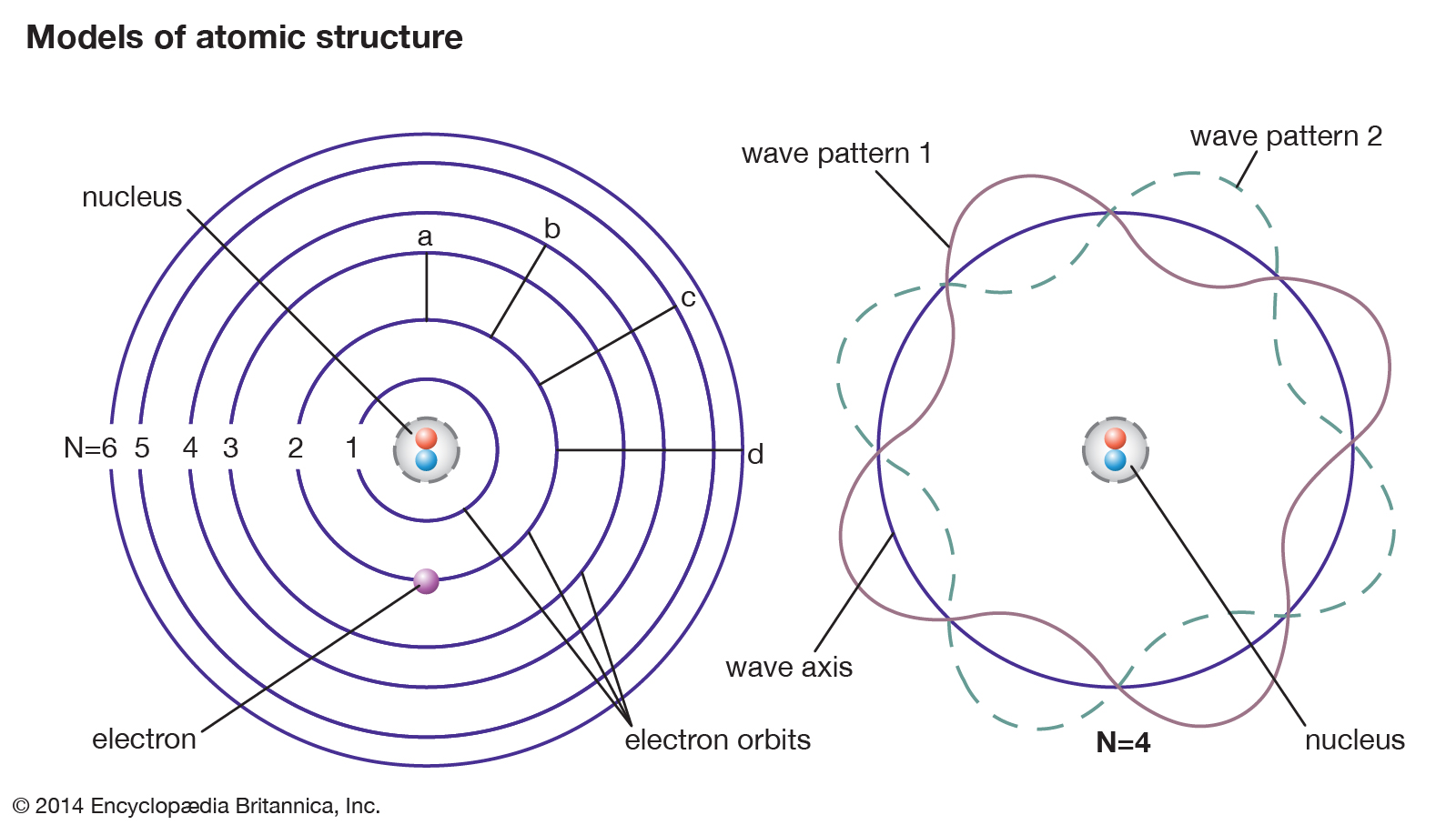
As anyone who remembers their basic chemistry or physics surely knows, atoms are composed of subatomic particles known as nucleons. These consist of positively-charged particles (protons) and neutral particles (neutrons) that are arranged in the center (in the nucleus). These are surrounded by electrons which orbit the nucleus and are arranged in different energy levels.

The reason why subatomic particles that have fundamentally different charges are able to exist so close together is because of the presence of Strong Nuclear Force – a fundamental force of the universe that allows subatomic particles to be attracted at short distances. It is this force that counteracts the repulsive force (known as the Coulomb Force) that causes particles to repel each other.
Therefore, any attempt to divide the nucleus into the same number of free unbound neutrons and protons – so that they are far/distant enough from each other that the strong nuclear force can no longer cause the particles to interact – will require enough energy to break these nuclear bonds.
Thus, binding energy is not only the amount of energy required to break strong nuclear force bonds, it is also a measure of the strength of the bonds holding the nucleons together.
Nuclear Fission and Fusion:
In order to separate nucleons, energy must be supplied to the nucleus, which is usually accomplished by bombarding the nucleus with high energy particles. In the case of bombarding heavy atomic nuclei (like uranium or plutonium atoms) with protons, this is known as nuclear fission.
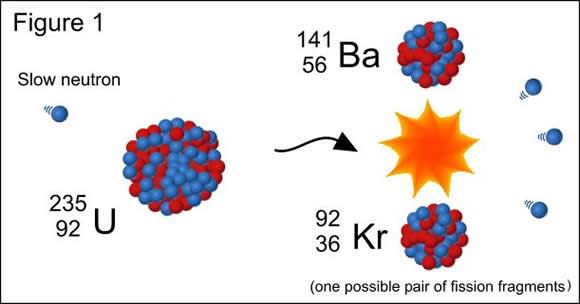
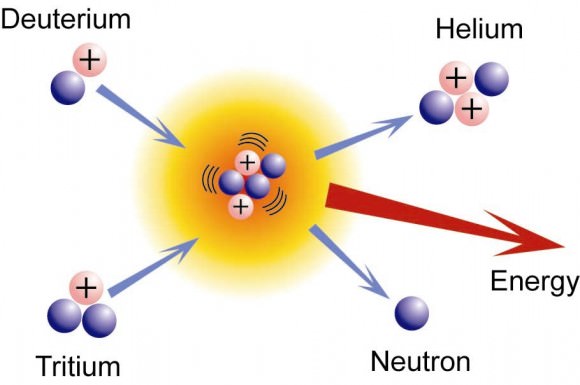
However, binding energy also plays a role in nuclear fusion, where light nuclei together (such as hydrogen atoms), are bound together under high energy states. If the binding energy for the products is higher when light nuclei fuse, or when heavy nuclei split, either of these processes will result in a release of the “extra” binding energy. This energy is referred to as nuclear energy, or loosely as nuclear power.
It is observed that the mass of any nucleus is always less than the sum of the masses of the individual constituent nucleons which make it up. The “loss” of mass which results when nucleons are split to form smaller nucleus, or merge to form a larger nucleus, is also attributed to a binding energy. This missing mass may be lost during the process in the form of heat or light.
Once the system cools to normal temperatures and returns to ground states in terms of energy levels, there is less mass remaining in the system. In that case, the removed heat represents exactly the mass “deficit”, and the heat itself retains the mass which was lost (from the point of view of the initial system). This mass appears in any other system which absorbs the heat and gains thermal energy.
Types of Binding Energy:
Strictly speaking, there are several different types of binding energy, which is based on the particular field of study. When it comes to particle physics, binding energy refers to the energy an atom derives from electromagnetic interaction, and is also the amount of energy required to disassemble an atom into free nucleons.
In the case of removing electrons from an atom, a molecule, or an ion, the energy required is known as “electron binding energy” (aka. ionization potential). In general, the binding energy of a single proton or neutron in a nucleus is approximately a million times greater than the binding energy of a single electron in an atom.
In astrophysics, scientists employ the term “gravitational binding energy” to refer to the amount of energy it would take to pull apart (to infinity) an object held together by gravity alone – i.e. any stellar object like a star, a planet, or a comet. It also refers to the amount of energy that is liberated (usually in the form of heat) during the accretion of such an object from material falling from infinity.
Finally, there is what is known as “bond” energy, which is a measure of the bond strength in chemical bonds, and is also the amount of energy (heat) it would take to break a chemical compound down into its constituent atoms. Basically, binding energy is the very thing that binds our Universe together. And when various parts of it are broken apart, it is the amount of energy needed to carry it out.
The study of binding energy has numerous applications, not the least of which are nuclear power, electricity, and chemical manufacture. And in the coming years and decades, it will be intrinsic in the development of nuclear fusion!
We have written many articles about binding energy for Universe Today. Here’s What is Bohr’s Atomic Model?, What is John Dalton’s Atomic Model?, What is the Plum Pudding Atomic Model?, What is Atomic Mass?, and Nuclear Fusion in Stars.
If you’d like more info on binding energy, check out Hyperphysics article on Nuclear Binding Energy.
We’ve also recorded an entire episode of Astronomy Cast all about the Important Numbers in the Universe. Listen here, Episode 45: The Important Numbers in the Universe.
Sources: