Illustration of how anti-hydrogen can test gravity. Credit: National Science Foundation
It’s a basic fact we’ve all learned in school. Drop any object, be it a baseball, feather, or cat, and it will fall toward the Earth at exactly the same rate. The cat will fortunately land on its feet thanks to a bit of feline grace, but the point is that everything falls at the same rate under gravity. It doesn’t matter what an object is made of, or how heavy it is. While we’ve all been taught this fact, calling it a fact was, until recently, a bit of a lie.
The ALICE detector on CERN's Large Hadron Collider. Credit: A Saba/CERN
For decades, astrophysicists have theorized that the majority of matter in our Universe is made up of a mysterious invisible mass known as “Dark Matter” (DM). While scientists have not yet found any direct evidence of this invisible mass or confirmed what it looks like, there are several possible ways we could search for it soon. One theory is that Dark Matter particles could collide and annihilate each other to produce cosmic rays that proliferate throughout our galaxy – similar to how cosmic ray collisions with the interstellar medium (ISM) do.
This theory could be tested soon, thanks to research conducted using the A Large Ion Collider Experiment (ALICE), one of several detector experiments at CERN’s Large Hadron Collider (LHC). ALICE is optimized to study the results from collisions between nuclei that travel very close to the speed of light (ultra-relativistic velocities). According to new research by the ALICE Collaboration, dedicated instruments could detect anti-helium-3 nuclei (the anti-matter counterpart to He3) as they reach Earth’s atmosphere, thus providing evidence for DM.
This image from NASA's Chandra X-ray Observatory and ground-based optical telescopes shows an extremely long beam, or filament, of matter and antimatter extending from a relatively tiny pulsar, as reported in our latest press release. With its tremendous scale, this beam may help explain the surprisingly large numbers of positrons, the antimatter counterparts to electrons, scientists have detected throughout the Milky Way galaxy. Image Credit: X-ray: NASA/CXC/Stanford Univ./M. de Vries; Optical: NSF/AURA/Gemini Consortium
Why is there so much antimatter in the Universe? Ordinary matter is far more plentiful than antimatter, but scientists keep detecting more and more antimatter in the form of positrons. More positrons reach Earth than standard models predict. Where do they come from?
Scientists think pulsars are one source, and a new study strengthens that idea.
Astronomers have been watching a nearby pulsar with a strange halo around it. That pulsar might answer a question that’s puzzled astronomers for some time. The pulsar is named Geminga, and it’s one of the nearest pulsars to Earth, about 800 light years away in the constellation Gemini. Not only is it close to Earth, but Geminga is also very bright in gamma rays.
In 1924, French physicist Louis de Broglie proposed that photons – the subatomic particle that constitutes light – behave as both a particle and a wave. Known as “particle-wave duality”, this property has been tested and shown to apply with other subatomic particles (electrons and neutrons) as well as larger, more complex molecules.
Recently, an experiment conducted by researchers with the QUantum Interferometry and Gravitation with Positrons and LAsers (QUPLAS) collaboration demonstrated that this same property applies to antimatter. This was done using the same kind of interference test (aka. double-slit experiment) that helped scientists to propose particle-wave duality in the first place.
A Kyoto University-based team has unraveled the mystery of gamma-ray emission cascades caused by lightning strikes. Credit: Kyoto University/Teruaki Enoto
Lighting has always been a source of awe and mystery for us lowly mortals. In ancient times, people associated it with Gods like Zeus and Thor, the fathers of the Greek and Norse pantheons. With the birth of modern science and meteorology, lighting is no longer considered the province of the divine. However, this does not mean that the sense of mystery it carries has diminished one bit.
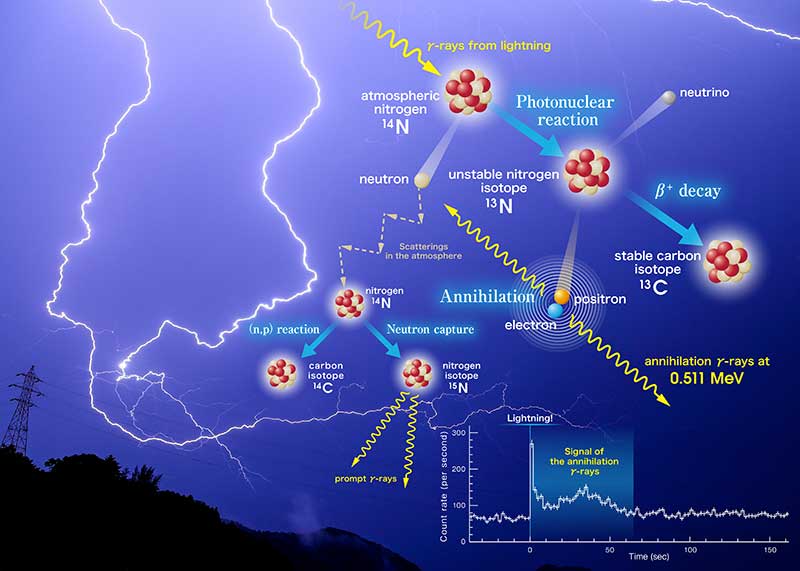
For example, scientists have found that lightning occurs in the atmospheres of other planets, like the gas giant Jupiter (appropriately!) and the hellish world of Venus. And according to a recent study from Kyoto University, gamma rays caused by lighting interact with air molecules, regularly producing radioisotopes and even positrons – the antimatter version of electrons.
The study, titled “Photonuclear Reactions Triggered by Lightning Discharge“, recently appeared in the scientific journal Nature. The study was led by Teruaki Enoto, a researcher from The Hakubi Center for Advanced Research at Kyoto University, and included members from the University of Tokyo, Hokkaido University, Nagoya University, the RIKEN Nishina Center, the MAXI Team, and the Japan Atomic Energy Agency.
For some time, physicists have been aware that small bursts of high-energy gamma rays can be produced by lightning storms – what are known as “terrestrial gamma-ray flashes”. They are believed to be the result of static electrical fields accelerating electrons, which are then slowed by the atmosphere. This phenomenon was first discovered by space-based observatories, and rays of up to 100,000 electron volts (100 MeV) have been observed.
Given the energy levels involved, the Japanese research team sought to examine how these bursts of gamma rays interact with air molecules. As Teruaki Enoto from Kyoto University, who leads the project, explained in a Kyoto University press release:
“We already knew that thunderclouds and lightning emit gamma rays, and hypothesized that they would react in some way with the nuclei of environmental elements in the atmosphere. In winter, Japan’s western coastal area is ideal for observing powerful lightning and thunderstorms. So, in 2015 we started building a series of small gamma-ray detectors, and placed them in various locations along the coast.”
Unfortunately, the team ran into funding problems along the way. As Enoto explained, they decided to reach out to the general public and established a crowdfunding campaign to fund their work. “We set up a crowdfunding campaign through the ‘academist’ site,” he said, “in which we explained our scientific method and aims for the project. Thanks to everybody’s support, we were able to make far more than our original funding goal.”
Thanks to the success of their campaign, the team built and installed particle detectors across the northwest coast of Honshu. In February of 2017, they installed four more detectors in Kashiwazaki city, which is a few hundred meters away from the neighboring town of Niigata. Immediately after the detectors were installed, a lightning strike took place in Niigata, and the team was able to study it.
What they found was something entirely new and unexpected. After analyzing the data, the team detected three distinct gamma-ray bursts of varying duration. The first was less than a millisecond long, the second was gamma ray-afterglow that took several milliseconds to decay, and the last was a prolonged emission lasting about one minute. As Enoto explained:
“We could tell that the first burst was from the lightning strike. Through our analysis and calculations, we eventually determined the origins of the second and third emissions as well.”
They determined that the second afterglow was caused by the lightning reacting with nitrogen in the atmosphere. Essentially, gamma rays are capable of causing nitrogen molecules to lose a neutron, and it was the reabsorption of these neutrons by other atmospheric particles that produced the gamma-ray afterglow. The final, prolonged emission was the result of unstable nitrogen atoms breaking down.
It was here that things really got interesting. As the unstable nitrogen broke down, it released positrons that then collided with electrons, causing matter-antimatter annihilations that released more gamma rays. As Enoto explained, this demonstrated, for the first time that antimatter is something that can occur in nature due to common mechanisms.
“We have this idea that antimatter is something that only exists in science fiction,” he said. “Who knew that it could be passing right above our heads on a stormy day? And we know all this thanks to our supporters who joined us through ‘academist’. We are truly grateful to all.”
If these results are indeed correct, than antimatter is not the extremely rare substance that we tend to think it is. In addition, the study could present new opportunities for high-energy physics and antimatter research. All of this research could also lead to the development of new or refined techniques for creating it.
Looking ahead, Enoto and his team hopes to conduct more research using the ten detectors they still have operating along the coast of Japan. They also hope to continue involving the public with their research, a process that goes far beyond crowdfunding and includes the efforts of citizen scientists to help process and interpret data.
Artist's impression of a cloud of trapped antihydrogen atoms. Credit: CERN/Chukman So
Ever since the existence of antimatter was proposed in the early 20th century, scientists have sought to understand how relates to normal matter, and why there is an apparent imbalance between the two in the Universe. To do this, particle physics research in the past few decades has focused on the anti-particle of the most elementary and abundant atom in the Universe – the antihydrogen particle.
Until recently, this has been very difficult, as scientists have been able to produce antihydrogen, but unable to study it for long before it annihilated. But according to recent a study that was published in Nature, a team using the ALPHA experiment was able to obtain the first spectral information on antihydrogen. This achievement, which was 20 years in the making, could open up an entirely new era of research into antimatter.
Measuring how elements absorb or emit light – i.e. spectroscopy – is a major aspect of physics, chemistry and astronomy. Not only does it allow scientists to characterize atoms and molecules, it allows astrophysicists to determine the composition of distant stars by analyzing the spectrum of the light they emit.
The ALPHA experiment probes whether matter behaves differently from antimatter by measuring the antihydrogen spectrum with high-precision, further testing the robustness of the Standard Model. Credit: Maximilien Brice/CERN
In the past, many studies have been conducted into the spectrum of hydrogen, which constitutes roughly 75% of all baryonic mass in the Universe. These have played a vital role in our understanding of matter, energy, and the evolution of multiple scientific disciplines. But until recently, studying the spectrum of its anti-particle has been incredibly difficult.
For starters, it requires that the particles that constitute antihydrogen – antiprotons and positrons (anti-electrons) – be captured and cooled so that they may come together. In addition, it is then necessary to maintain these particles long enough to observe their behavior, before they inevitable make contact with normal matter and annihilate.
Luckily, technology has progressed in the past few decades to the point where research into antimatter is now possible, thus affording scientists the opportunity to deduce whether the physics behind antimatter are consistent with the Standard Model or go beyond it. As the CERN research team – which was led by Dr. Ahmadi of the Department of Physics at the University of Liverpool – indicated in their study:
“The Standard Model predicts that there should have been equal amounts of matter and antimatter in the primordial Universe after the Big Bang, but today’s Universe is observed to consist almost entirely of ordinary matter. This motivates physicists to carefully study antimatter, to see if there is a small asymmetry in the laws of physics that govern the two types of matter.”
ALPHA uses a magnetic trap to hold neutral atoms of antihydrogen and then subjecting them to spectrographic analysis. Credit: CERN
Beginning in 1996, this research was conducted using the AnTiHydrogEN Apparatus (ATHENA) experiment, a part of the CERN Antiproton Decelerator facility. This experiment was responsible for capturing antiprotons and positrons, then cooling them to the point where they can combine to form anithydrogen. Since 2005, this task has become the responsibility of ATHENA’s successor, the ALPHA experiment.
Using updated instruments, ALPHA captures atoms of neutral antihydrogen and holds them for a longer period before they inevitably annihilate During this time, research teams conduct spectrographic analysis using ALPHA’s ultraviolet laser to see if the atoms obey the same laws as hydrogen atoms. As Jeffrey Hangst, the spokesperson of the ALPHA collaboration, explained in a CERN update:
“Using a laser to observe a transition in antihydrogen and comparing it to hydrogen to see if they obey the same laws of physics has always been a key goal of antimatter research… Moving and trapping antiprotons or positrons is easy because they are charged particles. But when you combine the two you get neutral antihydrogen, which is far more difficult to trap, so we have designed a very special magnetic trap that relies on the fact that antihydrogen is a little bit magnetic.”
In so doing, the research team was able to measure the frequency of light needed to cause a positron to transition from its lowest energy level to the next. What they found was that (within experimental limits) there was no difference between the antihydrogen spectral data and that of hydrogen. These results are an experimental first, as they are the first spectral observations ever made of an antihydrogen atom.
Besides allowing for comparisons between matter and antimatter for the first time, these results show that antimatter’s behavior – vis a vis its spectrographic characteristics – are consistent with the Standard Model. Specifically, they are consistent with what is known as Charge-Parity-Time (CPT) symmetry.
This symmetry theory, which is fundamental to established physics, predicts that energy levels in matter and antimatter would be the same. As the team explained in their study:
“We have performed the first laser-spectroscopic measurement on an atom of antimatter. This has long been a sought-after achievement in low-energy antimatter physics. It marks a turning point from proof-of-principle experiments to serious metrology and precision CPT comparisons using the optical spectrum of an anti-atom. The current result… demonstrate that tests of fundamental symmetries with antimatter at the AD are maturing rapidly.”
In other words, the confirmation that matter and antimatter have similar spectral characteristics is yet another indication that the Standard Model holds up – just as the discovery of the Higgs Boson in 2012 did. It also demonstrated the effectiveness of the ALPHA experiment at trapping antimatter particles, which will have benefits other antihydrogen experiments.
Naturally, the CERN researchers were very excited by this find, and it is expected to have drastic implications. Beyond offering a new means of testing the Standard Model, it is also expected to go a long way towards helping scientists to understand why there is a matter-antimatter imbalance in the Universe. Yet another crucial step in discovering exactly how the Universe as we know it came to be.
One of the biggest mysteries in astronomy is the question, where did all the antimatter go? Shortly after the Big Bang, there were almost equal amounts of matter and antimatter. I say almost, because there was a tiny bit more matter, really. And after the matter and antimatter crashed into each other and annihilated, we were left with all the matter we see in the Universe.
You, and everything you know is just a mathematical remainder, left over from the great division of the Universe’s first day.
We did a whole article on this mystery, so I won’t get into it too deeply.
But is it possible that the antimatter didn’t actually go anywhere? That it’s all still there in the Universe, floating in galaxies of antimatter, made up of antimatter stars, surrounded by antimatter planets, filled with antimatter aliens?
Aliens who are friendly and wonderful in every way, except if we hugged, we’d annihilate and detonate with the energy of gigatons of TNT. It’s sort of tragic, really.
If those antimatter galaxies are out there, could we detect them and communicate with those aliens?
First, a quick recap on antimatter.
Antimatter is just like matter in almost every way. Atoms have same atomic mass and the exact same properties, it’s just that all the charges are reversed. Antielectrons have a positive charge, antihydrogen is made up of an antiproton and a positron (instead of a proton and an electron).
It turns out this reversal of charge causes regular matter and antimatter to annihilate when they make contact, converting all their mass into pure energy when they come together.
We can make antimatter in the laboratory with particle accelerators, and there are natural sources of the stuff. For example, when a neutron star or black hole consumes a star, it can spew out particles of antimatter.
In fact, astronomers have detected vast clouds of antimatter in our own Milky Way, generated largely by black holes and neutron stars grinding up their binary companions.
Wyoming Milky Way set. Credit and copyright: Randy Halverson.
But our galaxy is mostly made up of regular matter. This antimatter is detectable because it’s constantly crashing into the gas, dust, planets and stars that make up the Milky Way. This stuff can’t get very far without hitting anything and detonating.
Now, back to the original question, could you have an entire galaxy made up of antimatter? In theory, yes, it would behave just like a regular galaxy. As long as there wasn’t any matter to interact with.
And that’s the problem. If these galaxies were out there, we’d see them interacting with the regular matter surrounding them. They would be blasting out radiation from all the annihilations from all the regular matter gas, dust, stars and planets wandering into an antimatter minefield.
Astronomers don’t see this as far as they look, just the regular, quiet and calm matter out to the edge of the observable Universe.
That doesn’t make it completely impossible, though, there could be galaxies of antimatter as long as they’re completely cut off from regular matter.
But even those would be detectable by the supernova explosions within them. A normally matter supernova generates fast moving neutrinos, while an antimatter supernova would generate a different collection of particles. This would be a dead giveaway.
There’s one open question about antimatter that might make this a deeper mystery. Scientists think that antimatter, like regular matter, has regular gravity. Matter and antimatter galaxies would be attracted to each other, encouraging annihilation.
But scientists don’t actually know this definitively yet. It’s possible that antimatter has antigravity. An atom of antihydrogen might actually fall upwards, accelerating away from the center of the Earth.
The ALPHA experiment, one of five experiments that are studying antimatter at CERN Credit: Maximilien Brice/CERN
Physicists at CERN have been generating antimatter particles, and trying to detect if they’re falling downward or up.
If that was the case, then antimatter galaxies might be able to repel particles of regular matter, preventing the annihilation, and the detection.
If you were hoping there are antimatter lurking out there, hoarding all that precious future energy, I’m sorry to say, but astronomers have looked and they haven’t found it. Just like the socks in your dryer, we may never discover where it all went.
Could there be a mirror universe, where everything is backwards – and everybody has goatees? How badly do you need to bend the laws of physics to make this happen?
One of the great mysteries in cosmology is why the Universe is mostly matter and not antimatter. If you want to learn more about that specific subject, you can click here and watch an episode all about that.
During the Big Bang, nearly equal amounts of matter and antimatter were created, and subsequently annihilated. Nearly equal. And so we’re left with a Universe made of matter.
But could there be antimatter stars out there? With antimatter planets in orbit. Could there be a backwards Universe that operates just like our regular Universe, but everything’s made of antimatter? And if it’s out there, does it have to be evil? Do they only know how to conquer? Does everyone, even the antimatter babies and ladies, have handsome goatees? How about sashes? I hear they’re big on sashes. OOH and daggers. Gold daggers with little teensy antimatter emeralds and rubies.
Antimatter, without the goatee, was theorized in 1928 by Paul Dirac, who realized that one implication of quantum physics was that you could get electrons that had a positive charge instead of a negative charge. They were discovered by Carl D. Anderson just 4 years later, which he named “positron” for positive electron.
We believe he was clearly snubbing Dirac, by not naming them the “Diracitron”, alternately they were saving that name for a giant Japanese robot.
These antiparticles are created through high energy particle collisions happening naturally in the Universe, or unnaturally inside our “laugh in the face of God and nature” particle accelerators. We can even detect the annihilation out there in the Universe where matter and antimatter crash into each other.
Physicists have discovered a range of anti-particles. Anti-protons, anti-neutrons, anti-hydrogen, anti-helium. To date, there’s been no evidence of any goatees or sashes. Naturally, they wondered what might happen if the balance of the Universe was flipped. What if we had a Universe made out of mostly antimatter? Would it still… you know, work? Could you have antimatter stars, antimatter planets, and even those antimatter people we mentioned?
The Large Hadron Collider (CERN/LHC)
When physics swap out matter for anti-matter in their equations, they call it charge conjugation. It turns out, no. If you reversed the charge of all the particles in the Universe, it wouldn’t evolve in the same way as our “plain old non-sashed” Universe.
To fix this problem, physicists considered the implications if you had an actual mirror Universe, where all the particles behaved as if they were mirror images of themselves. This sounds a little more in line with our “Through a mirror, darkly” goatee and sash every day festival universe. This is all the bits backwards. Spin, charge, velocity, the works. They called this parity inversion. So, would this work?
Again, it turns out that the answer is no. It would almost work out, but there’s a tendency for the weak nuclear force, the one the governs nuclear decay to violate this idea of parity inversion. Even in a mirror Universe, the weak nuclear force is left-handed. Dammit, weak nuclear force, get your act together, if not just for the sake of the costumes and cooler bridge lighting.
What matter and antimatter might look like annihilating one another. Credit: NASA/CXC/M. Weiss
What if you reversed both the charge and the parity at the same time? What if you had antimatter in a mirror Universe? Physicists called this charge-parity symmetry, or CP symmetry.
In a dazzling experiment and absolute “what if” one-upmanship exercise by James Cronin and Val Fitch in 1964. They demonstrated that no, you can’t have a mirror-antimatter Universe evolve with our physical laws. This experiment won the Nobel Prize in 1980.
Physicists had one last trick up their sleeves. It turns out that if you reverse time itself as well as making everything out of antimatter and holding it up to a mirror, you get true symmetry. All the physical lays are preserved, and you’d get a Universe that would look exactly like our own.
It turns out we could live in a mirror Universe, as long as you were willing to reverse the charge of every particle and run time backwards. And if you did, it would be indistinguishable from the Universe we actually live in. Now, if you’ll excuse me, I think I need to call my tailor, I hear sashes are going to be huge this year.
So what do you think, do we live in the real Universe or the mirror Universe? Tell us in the comments below.
