
“Are the dilation calculations correct” the jump coordinator asks you as he approaches your desk. You look over some papers in front of you that contain various equations scribbled down with certain values circled. The equations are more for your own sense of security, as the computer console in front of you displays the same values you’ve circled. You look back up at the jump coordinator and reply,
“The numbers are solid and the contraction values are set for the trip. Helios II has a copy on board for their astrophysics department to review. Their cryo-engineers have already begun checking the nap-tubes to make sure they have the appropriate wake time in their reference frame.” The jump coordinator nods and walks over to the launch director of Lunar Launch Base Bravo (LLB Bravo). He leans over to relay this information to her and she nods while tapping the screen of her console.
“Helios II, this is LLB Bravo Command,” she barks into the comm, “Everything here checks out cleanly and you are clear for departure to the Andromeda galaxy. Safe travels and do humanity proud.” After she closes the comm she continues as if only to those nearest her, “Because humanity will likely not exist when you get there…” You look out the domed viewport and see the edge of a massive lunar crater which conceals the Helios II locked in on magnetic tracks that run the diameter of the depression. The tracks are a part of the electromagnetic launch system that eventually follows the curvature of the crater’s bowl upward and was developed for accelerating massive ships onto their trajectories (and out of the lunar gravity well) without the ship burning any of its fuel. You see the countdown timer holographically displayed on the dome glass tick down to zero and then disappear.

Without a sound, the magnetic tracks sequentially shift their polarity, launching the Helios II up the crater wall and off into space at a remarkable velocity. After a few moments, you see the engines light in the distance and the ship rockets towards their new home in Andromeda.
The remark from the commander then hits you. Yes, in school you always worked with the idea of time dilation and length contraction when studying and testing, but the reality of it still packs a punch; when the crew of the Helios II arrives at their future destination, humanity could either be very different, or may not exist at all. Reality itself seems very strange when you actually begin to study and apply how it works. The notion that those few thousand human beings could be the only human beings in the universe upon arrival in Andromeda is shocking to say the least.
How is this possible? What are dilation calculations and how does that link to our species on Earth not existing when our brave travelers arrive in Andromeda? What is this contraction value that was mentioned? These are the questions that I will seek to answer in this article. What I have provided in this introduction is a fun but haunting look at the ramifications of what we know as Special and General Relativity.

It was, of course, Albert Einstein at the beginning of the 20th century who postulated a rather wild idea: that Isaac Newton was wrong about gravity and the nature of space and time. It was also Albert Einstein who attempted to answer the question “what is light?” These three things don’t appear to be linked, but once you begin to study physics (and of course after reading this article) you cannot help but see that light, time, and gravity are intertwined entities.

Credit: National Library of Austria/F Schmutzer/Public Domain
The nature of the universe, the very reality you exist in, behaves in ways that go against every notion of common sense you evolved to have.
There are many ways to tackle the strange nature of Einstein’s relativity, and most of them rely on mind-bending explanations paired with rigorous mathematical treatments. I will attempt to distill the core ideas down to something that doesn’t require extensive mathematics as a way of demonstrating how time dilation and length contraction works. Also worth noting, I will be avoiding the use of General Relativity so as to not get caught up with the intense mathematics needed for such examples. That being said, the scenarios I am using exist within Special Relativity, as this is generally where most physics students first encounter these fantastic ideas.
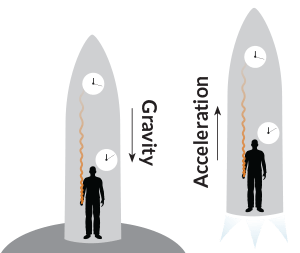
The very first thing to discuss is something that Einstein postulated that will help me further explain the aforementioned concepts. This is what is known as the Equivalence Principle. What it boils down to is a way of saying that someone’s gravitational mass is the same as their inertial mass , and that a force on a mass in a gravitational field like on the Earth’s surface is the same as a force on a mass in an accelerated reference frame, like when you hit the accelerator in your car and you feel “something” push you back. The way of showing that these two different scenarios are in fact the same goes as follows:
First, we identify two frames of reference that we will carry out experiments in. These situations will be in a ship both in open space and on the surface of Earth with a gravitational force (the acceleration due to gravity being 9.8 ). With you in the ship is a ball and a small hole in the wall. First consider the ship on Earth experiencing gravity. You would feel yourself pressed to the floor of the ship and if you picked up the ball and let it go, you would observe the ball fall to the floor at a rate of 9.8
.
Credit: E. Otwell
If you repeated this ball drop experiment in the ship that is in open space, the ball would simply “float” in front of you. Let’s now accelerate this ship “upwards” at a rate of 9.8 and observe the ball. The ship would rush upwards and meet your feet causing you to be pressed to the floor, and if you let the ball go, you would see the ball rush “downward” and hit the floor, just as it did when your ship was on the surface of the planet.
If neither ship had any windows so that you couldn’t determine whether you were in open space or on Earth, then there would be no way for you to differentiate between the two scenarios based on your experimental results. With an idea similar to this in mind, Einstein claimed that the effects of gravity and acceleration were the same thing. This was a crucial step in furthering our understanding of gravity, light, and time.
Now we turn our attention to the small hole in the wall of the ship. From outside, a pulse of light from a laser flashes through the hole. While you are in open space and not accelerating, this beam of light would travel in a straight line across the ship and impact the wall directly opposite of the hole. Now, let’s accelerate this ship “upwards” and observe what happens. With the ship accelerating “upwards” as it was during the ball drop experiment, the beam of light enters the hole in the wall. Since the photons (light is both a wave and a particle, and these particles are called photons) that make up the light beam are traveling at a constant velocity across the ship, and the ship is accelerating “upwards”, the spot on the wall where the photons would impact would appear to drop below where the hole is on the opposite wall.
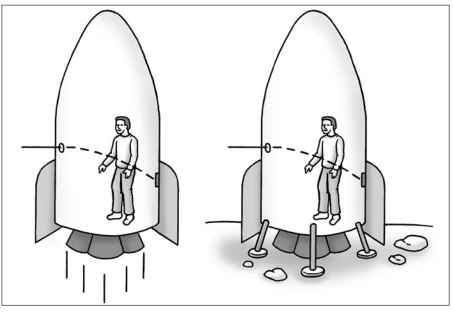
To you in the ship, the light would appear to bend downwards in the presence of the accelerated frame of reference. Now recall what we already established with the Equivalence Principle and the ball drop experiment. Someone in a ship in open space accelerating upwards at a rate of 9.8 would experience the same physics as someone stationary on Earth’s surface. So that would mean that if you observe light bending in the ship that is accelerating in open space, then you must also observe light bending in the ship that is on Earth’s surface. But is this true? Does light actually bend when in the presence of a gravitating body? The short answer is yes, but to establish why we must first discuss space and time, and how they are intimately linked.
Einstein truly was a man beyond his time; his mind was able to reach out of the known and visualize what nobody else had. He arrived at the idea that space and time were connected (Hermann Minkowski, a brilliant mathematician and one of Einstein’s former professors, was the first to link space and time together geometrically and called it spacetime, which later Einstein used to complete his theory) and that the warping of this is what causes what we measure to be gravity. But how can we visualize this to help with understanding this amazing discovery? The most useful way that I visualize spacetime and how it interacts in such a way as to produce the bending of light is with yet another thought experiment. We’ll need a large, circular rubber sheet (sort of like a trampoline), a heavy ball, a marble, and a friend. Now, imagine the rubber sheet is pulled tight at the edges; this is spacetime. Without anything on it, it is flat. Have your friend stand opposite of you and then take the marble and roll it towards them; the marble representing a photon. What your friend observes is the marble rolling to them in a straight line.
Now, place the heavy ball in the center of the sheet; the ball being a massive body like the earth or the sun. What you and your friend observe is the ball sinking down into the sheet and creating a sort of well; this well is what we experience as gravity!

Credit: Stanford University.
Let’s yet again roll the marble to your friend, except this time with the ball warping the sheet. If you roll the marble sufficiently fast enough, it will dip into the well, roll around the inner well wall a bit, and then up and out of the well. Depending on how fast you rolled the marble, or how deep the well is, will affect where the marble exits the other side. Your friend will see where you initially rolled the marble, but where it exits the well won’t necessarily be opposite of where you stand. The marble will have deflected onto a new trajectory. Keeping this visual in mind, you can now somewhat grasp how light would appear to bend in the presence of gravity! For the light, it is traveling in a straight line, but if spacetime itself is curved the light will follow that curvature.
Credit: Physics Stack Exchange
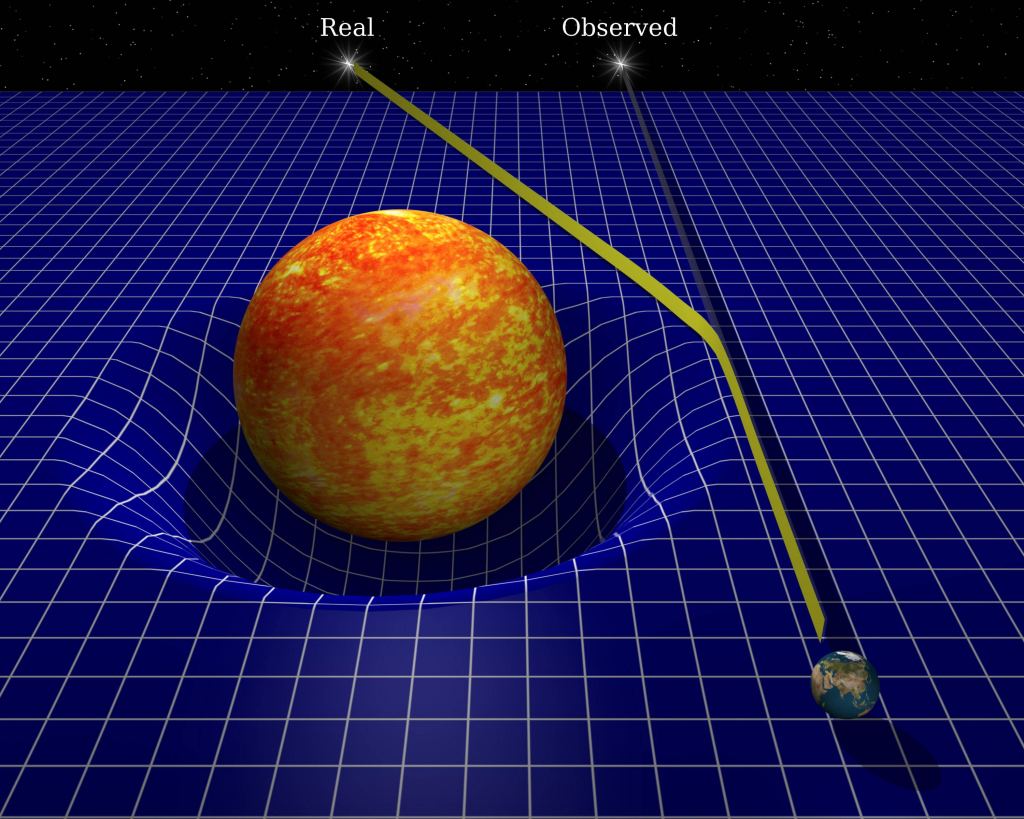
You may ask, “But how can we not see this bending of light on Earth? The Earth is huge and so light should be bending all around us!” Well, actually it does. But it is such a small deviation that it goes unnoticed. Think back to the scenario presented with the sheet: depending on how fast the marble was rolling, or how deep the well was, this would determine where the marble exits the well. In reality, light is traveling extremely fast, and that value is fixed for all observers (something we’ll cover shortly). Meaning that the only thing that determines how much the light is deflected by as seen by an observer (like your friend) is how deep the well is in spacetime (called a gravity well) that the light interacts with. Since light is so fast, you would need an incredibly deep gravity well to notice this curvature.
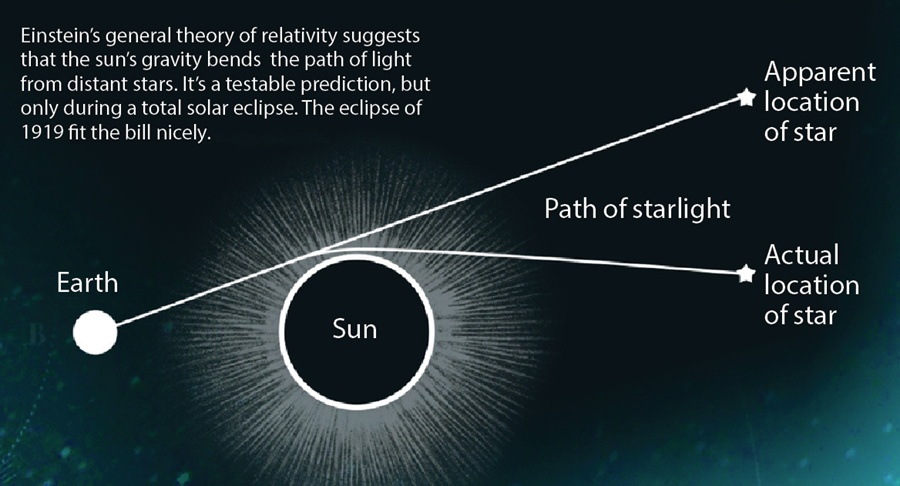
This is exactly what Einstein knew when he postulated this idea. He knew that he would need something with much more mass than the Earth to ever be able to see light bend with the technology he had available at that time. He recognized that our sun would have sufficient mass to produce a gravity well deep enough to create a noticeable deflection of light. And what would be supplying the light to be measured? Distant stars. But the only way to actually image stars around the sun was during a total solar eclipse. For this, he turned to the astronomer Sir Arthur Eddington. The story of how Einstein was able to get both his theory’s prediction and his desired experimental test to Eddington was remarkable by itself given World War 1 was in full swing during this time.

Both he and Eddington happened to be living in rival nations at war (Germany and England respectively), meaning communication directly between the two was impossible, not to mention Eddington trying to convince his rabidly patriotic colleagues and government to fund an expedition to test an “enemy” theory. However, in the end, both Einstein’s and Eddington’s internationalist and pacifist ideals prevailed, and Eddington was able to carry out the experiment required to prove what Einstein was claiming.
This experiment required the sun’s mass to show a visible deflection of star light passing very close to the sun from our perspective and the only way to do this was during a total solar eclipse. The eclipse mechanism was merely to block out the light from the sun so that Eddington could get pictures of the stars around the sun to see if the sun’s mass changed their apparent positions due to the warping of spacetime.
Credit: Discover Magazine, GFSC/NASA
The experiment was a success in that Eddington and company saw that the stars that appeared very close the sun had their apparent positions shifted by the amount predicted by Einstein’s calculations, thus confirming that gravity did indeed bend light. Einstein was correct in his view of how gravity and light interacted.
Having provided a way to visualize Einstein’s perspective on gravity and spacetime, we can get to the original questions purposed by our futuristic scenario at the beginning of this article. I talked of dilation calculations and contraction values. The obvious question is, “Does time and space really dilate and contract?” It all stems from an observation that existed in the world of physics that Einstein thought to reconcile. Up until the early 1900s, physics was dominated by two very big ideas. These ideas came from Isaac Newton and James Maxwell.

Credit: Isaac Newton Institute
Isaac Newton, when forming his theory on gravity and motion, stated that time and space were absolute and unchanging for all observers. At the beginning of his seminal paper, Principia Mathematica, he defined time to pass equally for all things and essentially to be invariant to all ways of measuring it. Likewise, he also defined space to be immovable and unchangeable; an absolute to measure positions against. These were crucial definitions when forming his mathematical treatments for how massive bodies interacted gravitationally.
James Maxwell, often referred to as the father of electromagnetic theory and one of the most important natural philosphers to have ever lived, developed the mathematical framework that describes how electricicy and magnetism behaves. His approach involved modeling both of these physical systems using fields that interacted with each other in intrinsic ways, showing that they were both a part of the same process. One of the products of these interactions was something he called electromagnetic waves, and in studying them he discovered something amazing. The velocity of these waves were exactly what we measured the speed of light to be: approximately 300,000,000 (671 million mph). This was no coincidence, and he later went on to prove that light itself was an electromagnetic wave. A curious consequence of how his mathematical laws worked implied that light traveled at only one speed regardless of relative motion. The amazing realization that his math eventually led to was that even if someone was moving relative to someone else and emitting light, both people would measure that light to be the same speed, meaning that you wouldn’t see the light moving “faster” because someone was moving faster than you while emitting said light.

Credit: Public Domain
This was a direct contradiction with Newtonian physics which stated that velocities of objects being measured added and subtracted dependent on their relative motion. Despite this discrepancy between these two leading theories being known, it would take a genius to work out a way to either reconcile the two, or to declare one the victor and reside the other to defeat. To elucidate the issue between these two theories, I will use a thought experiment developed by Einstein and illustrated in his work describing Special Relativity.
Imagine two friends, one named X and the other Y. Y is standing at a train station during a thunderstorm and X is on the train. The train approaches the station at a high speed, and as it is passing, two lightning bolts strike the ground, one in front of the moving train and the other behind it (bolts A and B respectively). These strikes coincide with the moment that both Y and X are across from each other. From the perspective of Y, both lightning bolts A and B hit the ground at the same time; the light from each bolt traveling the same distance to reach Y simultaneously. But on the train, X is moving towards bolt A and away from bolt B. As such, the light from bolt A has a shorter distance to travel and the light from bolt B has a longer distance to travel. Therefore, X sees the bolts strike at different times. So which is it? Did the lightning bolts hit the ground at the same time, or at different times?
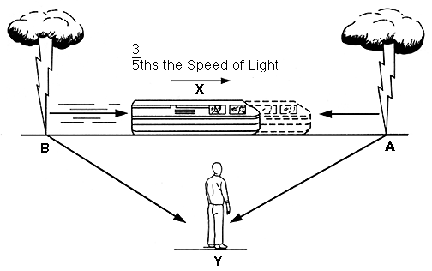
Credit: Unknown artist
Consider this carefully; our two conflicting postulates are that time and space are absolute (Newton), and that the speed of light is the same speed for all observers regardless of relative motion (Maxwell). Y would measure the time of both lightning bolt strikes to be simultaneous, as the time they hit would occur at one specific time on their watch, say at 4pm and 10 seconds. If time and space are absolute, then X must also measure the lightning bolt strikes as both occurring at 4pm and 10 seconds. But if the speed of light is a fixed value for all observers regardless of motion, X has to see bolt A strike first, say at 4pm and 9 seconds, and then bolt B strike second at 4pm and 11 seconds. In order for X to make a measurement of both bolts striking at the same time, bolt B’s light would have to travel faster than bolt A’s light in order to reach X’s position at the same time. In order to maintain Newton’s postulate that time and space are absolute for all reference frames, the speed of light must vary. But if the speed of light is fixed and the same for all reference frames, Maxwell’s discovery, then that must mean that time and space must vary.
So who wins this titanic battle, Newton or Maxwell? To answer this, Einstein proposed (and later proved) something he called the Relativity of Simultaneity. Both observers were correct in their frame of reference due to the speed of light being fixed. Y saw the bolts hit the ground at the same time because the light traveled to Y’s position across an unchanging distance at a set velocity. However, from the perspective of X, the bolts struck at different times due to the motion of X with respect to Y. Light from bolt A got to X first as the reference frame of X (the train) was moving towards that bolt, and moving away from bolt B, thus B striking second.

Credit: Public Domain
Relativity of Simultaneity showed that different frames of reference have their own, independent measure of time and space. Simultaneous events in one frame of reference do not necessarily take place simultaneously in another, with the variable being the velocities between the two reference frames. It was in this way that Einstein showed that Maxwell’s mathematical consequences for the speed of light (it being the same for all observers regardless of relative motion) was correct, and that measurements of time and space must be different for different observers based on their relative motions to one another. Newton had been toppled.
Einstein began approaching his ideas mathematically by removing time from the constant column and allowing it to vary depending on the frame of reference that the measurements were taking place in. He showed that time could vary and could no longer be said to be absolute. What came along with this was that space itself was also no longer absolute, and could vary accordingly depending upon frame of reference. All of this varying of space and time comes down to how fast an object is moving relative to other objects. In essence, what Einstein had done was show that there was no preferred frame of reference that was “at rest” with respect to the universe by which to make all measurements from; light was the only constant in all reference frames, and thus we needed to make our measurements considering the speed of light as unchanging- this forces space and time to vary.
This is a lot to take in at first. Admittedly, it still can confuse me at times and I am a graduated physicist. There are a lot of paradoxes that would seem to arise from these amazing revelations about space and time being variant. However, upon closer inspection and moving these paradoxes into the realm of General Relativity, which is the theory that describes all that talk from before about the warping of spacetime, you actually see that these paradoxes melt away. Remember again that mass warps spacetime and this affects light (our rubber sheet and bowling ball scenario from earlier). This warping of space also means that it can warp time being that they are intimately connected.
To connect this idea into the moving reference frames discussed above with our friends Y and X, we look at mass and energy. Mass warps spacetime, and via (we owe this to Einstein as well), we see that mass and energy are equivalent. This means that both mass and energy can contribute to the warping of spacetime, or rather the effect we call gravity. When a massive body accelerates it gains energy; the faster you accelerate it, the more energy it gains. Therefore, this acceleration adds to the warping of spacetime.

The warping of spacetime is what causes the relativistic effects we have discussed (time and space varying, and light deflecting) These concepts are all linked and are fairly complex subjects to discuss. The actual nature of acceleration warping spacetime has to do with mathematical constructs and frames of reference within those constructs, topics that we will not attempt here. However, when you apply these ideas (oversimplified to say the least) to the various scenarios and paradoxes that naturally arise from Special Relativity, you arrive at the correct conclusions and the paradoxes resolve.
If all of this seems too unreal for you, recognize that the relativistic effects of time and space changing depending on motion or gravity come into play in most of our everyday lives. Our GPS satellites operate much further away from the earth’s surface than you or me. They are also traveling very fast compared to you or me. In order for GPS to work, it has to know your exact position, where you are going, and how long it will take for you to make that trip based on those two parameters. Its timing has to be set to match yours. If we didn’t account for the relativistic effects at work (the satellite’s clock ticks at a different rate than yours due to its velocity and distance away from earth) your GPS wouldn’t be accurate and you would never get to where you wanted to go!
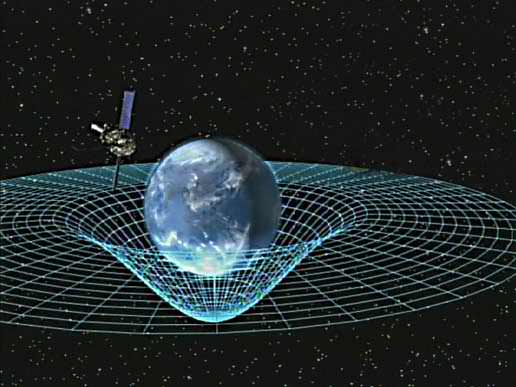
Credit: space.com Image credit: NASA
These relativistic calculations are implemented into the satellite’s programming to account for the difference in the flow of time it experiences.
Where does this leave us with our initial futuristic vision? I spoke of a dilation calculation for the ship that would be heading out towards the Andromeda galaxy. I mentioned the correct time being implemented for the cryo-tubes based off of frame of reference. To demonstrate the strange reality of reality, we will use a simplified, ideal situation. By simplified, I mean that we will set up our question with respect to the rules of Special Relativity, and use the two following equations:
Length Contraction
Time Dilation
Therefore, we will not be considering the acceleration of the Helios II to get up to speed, thus avoiding the peculiarities required by Einstein’s Field Equations that describe General Relativity.
Credit: Public Domain
But fear not, this is actually a common way of introducing the strange nature of time and space to young physicists, and the results of our equations listed above are just as valid so long as the physical situation being described remains simplified (constant velocity).
The Helios II has launched and arrived at a velocity of nearly the speed of light, say 2.9999999 (about 99% the speed of light). We also know the distance from Earth to the Helios II’s destination, Andromeda; roughly 2.5 million lightyears. We can now begin inputting what we know into our equations. For clarity, let’s break the time equation down so we know what each value stands for:
t = time experienced by people on Earth
t’ = time experienced in the Helios II
v = velocity of the Helios II
c = the speed of light
Given what we know (the time that the trip will take to Andromeda as experienced on Earth, t, and the speed of the Helios II, v) we can rearrange our time equation for the value we need; how long will the passengers need to stay asleep from their frame of reference, t’:
We can now plug in t and v and witness just how strange our universe really is. What we discover is that even though roughly 2.5 million years passes on Earth, for the crew of the Helios II a little more than 655 years pass. You read that correctly: the cryo-pods on the ship will only be programmed to keep the crew asleep for 655 years, but yet for humanity back on Earth, more than 2.5 million years will elapse.

Credit: Official SpaceX Photos, Flickr
Let this sink in a bit; what will only amount to a few centuries of time for the Helios II will be more than half the time the entire Earth has existed for humanity back in our solar system. But things get even more strange.
You may be thinking, “How can the time be shorter if the Helios II traveled 2.5 million lightyears? That would mean they had to have traveled faster than the speed of light!” Remember, time and space are linked in such a way that these sorts of strange scenarios manifest. The other equation that was mentioned above, the Length Contraction equation, now comes into play. We can break that one down for clarity as well:
l = distance to the Andromeda galaxy as measured from earth
l’ = distance the Helios II measures to the Andromeda galaxy at velocity
v = velocity of the Helios II
c = speed of light
When plugging in the known values (l and v), we arrive at a startling conclusion: that the distance traveled by the Helios II was only around 655 lightyears. Meaning that moving at near the speed of light, it takes them a little more than 655 years to make that trip. And yes, space physically contracted for the Helios II. This is a measured phenomena that has been physically proven using muons (subatomic particles) and how they arrive at the surface of the Earth after being created in the upper atmosphere.
As the title of this article suggests, reality is very strange. This also leads us to some philosophical speculation. Let’s just imagine we have the technology to accelerate a futuristic ship up to 99.99999% the speed of light (ignoring physical constraints).

Credit: NASA
In fact, let us even assume we have the ability to asymptotically approach the speed of light. What you find is that as the ship approaches the speed of light, the time experienced on it will get shorter and shorter. 655 years. 25 years. 1 year. 1 month. 1 day. 1 second. From the perspective of someone on the Earth, at least 2.5 million years must pass until our ever-faster ship arrives at the Andromeda galaxy. But on the ship, the faster it goes, the slower and slower time will move according to our Earth-bound observer.
Flip this perspective now to someone on the ship. For them, time is running as it should; their clocks are ticking away normally, their biological processes are functioning appropriately, and the length of movies would be the same as if they were stationary on Earth. But for them, the universe itself has contracted in size (at least ahead of them). The faster their ship rips through the universe, the shorter their trip through the universe becomes. 655 lightyears. 25 lightyears. 1 lightyear. 100 miles. 10 miles. 1 mile. For our crew on the ship, the universe itself seems to be collapsing in front of them.
Still with me?
Now, imagine for a moment that you are riding a light beam. You are fixed on a photon emitted during the Big Bang. For someone on Earth, they would see you and conclude that you have been traveling for 13.8 billion years, traveling across trillions of miles, from the moment of your creation until the moment you fell upon their inquisitive eye. But for you, for the photon, no time would have passed.

Credit: Screenshot of video simulation of light, Encyclopedia Britannica, Contunico ZDF Enterprises,
As discussed above, the faster you move through space, the slower you move through time, and the shorter space becomes for you. Therefore, at the speed of light, time simply stops, and space contracts to zero length in front of you. For you, the concept of a universe ceases to exist, because the moment your photon is created is the moment it is absorbed.
This is quite the amazing revelation when you take the concepts of relativity to the limit. Of course, this is merely a thought experiment as a photon carries with it no awareness of what time or space is, and we can never go the speed of light. In fact, getting up to the speed that I used earlier in my example seems fairly improbable. But in order to demonstrate to you just how strange reality is, one must use the rules in ways that reveal things often unseen in our day to day existence.
But ponder with me for one more moment. Journey with me to the edge of infinity. Let us place ourselves in the distant future where humanity has worked out a way to move our ships through the universe at these incredible velocities. Imagine that you are a crew member of the Helios II, being awoken 655 years after you were frozen in your cryo-pod. You would look out at the alien starfield from your quarters, wondering what people on Earth were thinking. Earth. The thought strikes you that 655 years has passed. This is an astounding thing to contemplate.

Credit: Stuart Atkinson
You remember that it was a 645 year span between the Bubonic plague ravaging Europe in 1348 to when the Hubble Telescope was launched in 1991.
But wait, you’ve experienced 655 years; the people back on Earth have experienced roughly 2.5 million years. The span of 2.5 million years separates the first picture of a black hole ever taken in 2019 with the first known ancestor of humanity appearing on earth (homo habilis).

Credit: Event Horizon Telescope Collaboration
That realization is jarring. Fantastical velocities and not-yet-known technologies aside, the idea that as we venture out into the cosmos at ever-increasing speeds, we will not only be placing vast distances in space between ourselves, but also vast distances in time. If we figure out near-lightspeed travel, what will emerge will be pockets of humanity, separated in such a way that a departing colony ship from one world will arrive and settle a new world knowing that the colony they left behind may not exist as they know it anymore. For the Helios II, Earth may have long forgotten about their journey, and even more tragic yet, humanity may not look or behave as human beings at all. Humanity may no longer exist on Earth, perhaps becoming a fossil record for some unknown species to evolve after us. Earth, as the crew of the Helios II remembers it, would be gone and the crew would be echoes of a species long forgotten by our home world.
The nature of relativity, and the strange reality of reality, shows that the further and faster we travel, the more we will separate ourselves from each other and fade into the background noise of the universe; wandering ghosts of a world that existed far away in space and time.

Credit: Battlestar Wiki Media


Nicely written. It’s so fun to imagine.
Thanks Joshua;
very informative article.
It appears somewhat surprising that Maxwell did not make the jump to special relativity, considering it seems to be an almost natural follow-on from the theories he did construct.
Very well-written article.