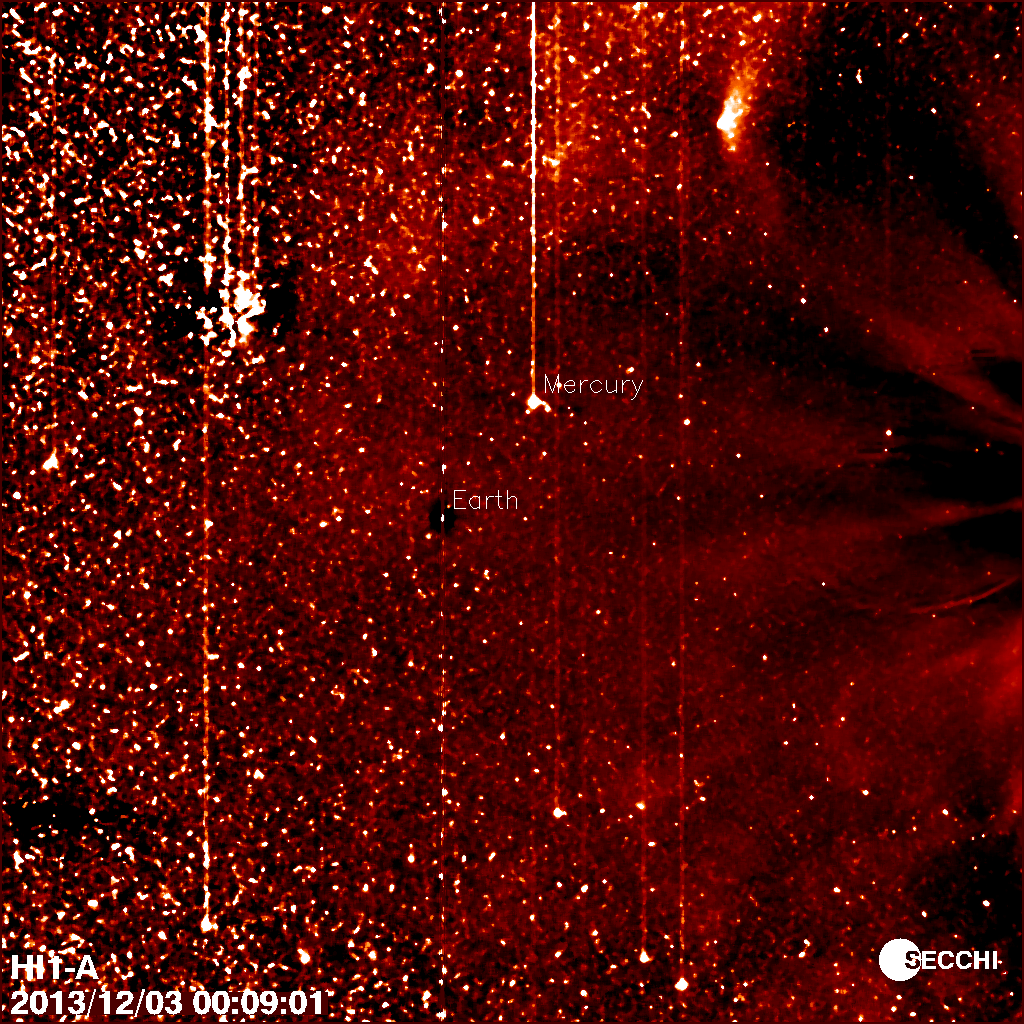
Could Comet ISON possibly still be alive? The latest high-resolution images available from the STEREO spacecraft are still showing some remains of the comet, although each day seems to show less and less activity. “If anything of ISON’s nucleus is left, it’s an inactive husk of a nucleus now,” Karl Battams from the Comet ISON Observing Campaign told Universe Today. “The comet remnant is fading fast in the STEREO data.”
Casey Lisse, also from CIOC was a bit more hopeful. In a web posting yesterday (Dec. 4) he said, “At this time, scientists are not sure how much of the comet survived intact. We may be seeing emission from rubble and debris in the comet’s trail, along its orbit, or we may be seeing the resumption of cometary activity from a sizable nucleus-sized chunk of ISON.”

Lisse added that most astronomers agree that Comet ISON was destroyed (with greater than 90% probability of this having occurred), leaving behind small (less than 10 m radius from the original 1 km nucleus) pieces of rubble, but there could be fragments 100 meters radius or larger. This would be big enough for astronomers to study but probably not big enough to provide a nice sky display later in December that everyone was hoping for.
Here’s the schedule of events for spacecraft to study whatever is left of Comet ISON, according to Lisse:
– NASA will monitor the comet for the next several weeks. If there is nothing sizable and stable left, it will dissipate and disappear in this time, as already emitted dust leaves the vicinity. If there is still a central source of emission, even if it is very much smaller, we will see a new, much fainter coma and tail form, which currently may be overwhelmed by the dust emitted from before the disruption event.
– NASA’s STEREO spacecraft will be using their cameras to search for bright fragments throughout the week, while the NASA Infrared Telescope Facility (IRTF) in Honolulu, Hawaii will use its 3m wide telescope to detect the comet spectroscopically, the same way it did on ISON’s inbound journey. Radio telescopes around the world will also be able to tell us more about what has happened. NASA’s recently launched MAVEN spacecraft may try to observe ISON next week. By mid- to late-December NASA’s Hubble and Chandra observatories will be performing deep outer space searches for any remnants of the comet. Spitzer will also look for ISON in early 2014.
If a fragment that acts like a comet is detected, but at a much reduced level, it may be hard to see it from the Earth at the time of its closest approach on December 26, 2013.
You can find out the latest on what is going on with ISON tomorrow, Dec. 6, 2013 as the CIOC is holding a post-perihelion workshop to discuss the status of the comet. The morning sessions, live from theh Applied Physics Lab at Johns Hopkins University will be webcast from approximately 8:30 am EST to 11:30 am EST, will be available for viewing in the player below:
More details on the meeting are available here.
So far, 12 spacecraft and the International Space Station have observed and detected Comet ISON on its multi-million year journey from the Oort Cloud to the solar corona. You can find out more about the planned Hubble observations here.

To combat the non-Euclidean relativist con game, I have decided to introduce THE CONE GAME! Reports were that a once in a lifetime galactic fireworks display was due from Comet Ison. There is a moving 3-D model of the comet’s path, which also shows the path of the planets as the comet comes within earth’s orbit. Here is the link showing these orbits as well as the curved path of the comet, which is very nearly a conic section as is an ellipse. http://www.solarsystemscope.com/ison/
ARE YOU READY FOR THE CONE GAME? Given three or four sightings and reported positions of a comet, Gauss was able to calculate the path of the comet and predict future positions. He was able to do this by first recognizing that the path would be a curved path known as a conic section (the curve that would appear where a plane intersects a cone). It is interesting to compare the curves in a moving 3-D model using this idea that the path of the comet and of the planets in the model are conic sections. Can someone by just looking at the 3-D model figure out what type of conic section curve most nearly describes the comet’s path? The way I view it is that the top of the cone of an ice cream cone is a circle, which is where a plane cuts across the cone. If you imagine where a parallel plane cuts across the cone further down, the intersection is a smaller circle. Then if you imagine that plane tilted slightly, the intersection with the cone that had previously been that smaller circle becomes slightly elongated, which forms an ellipse. One of Kepler’s laws was that the path of a planet orbiting the sun is an ellipse. So ellipses describe the orbits of the planets in the model. Using your imagination, the more you tilt the plane that passes through the cone, the more elongated the ellipse where the plane intersects the cone becomes, until you tilt the plane so far that the plane is parallel to a straight line inside the surface of the cone; the intersection then becomes a U shape that passes up through the top of the cone. The curve with this shape is called a parabola, which is also a conic section. If you keep tilting the plane further though, it becomes a hyperbola: the plane is no longer parallel to a straight line in the surface of the cone, but the intersection of the plane and cone is still a U shape that passes up through the top of the cone.
Of course Gauss couldn’t have calculated the path of a comet using non-Euclidean geometry. If you are using coordinates or angle measurements, you are using Euclidean geometry because non-Euclidean geometry, including the Riemannian type, without Hilbert’s Theorem 8 [5 in earlier books] does not have coordinates and does not have the SAS triangle congruency theorem. If Gauss thought this could be done with non-Euclidean mathematics (with Theorem 8 in Hilbert’s time), then he would have failed to realize that would be based on self-contradicting geometry. And without the coordinates there is no basis for a mapping with a non-Euclidean ‘space.’ See the Facebook Note: https://www.facebook.com/notes/reid-barnes/the-rule-of-threes/646220272097217
A friend came over for our T-day feast last Saturday. She brought her Ukulele with her and said that she doesn’t have the time or will to try to learn playing it any more. Would I like to use it? Well yes… of course! Sooo… I’ve been learning how to play the 12 bar “Comet ISON blues”, in G. Asinging: “They said it would be big. That It would be really very swell! But little did we know and how could we tell? That the sun would cook this comet and leave but a shell. Ohhhh yeah… I’ve got the Comet ISON blues…” Or something like that? ~@; )
A friend of mine wrote…
Comet ISON
Went the way of the Bison,
When, around the Sun it
turned,
It got burned.