urbain le verrier Archives

September 11, 2015August 23, 2017 by Matt Williams

The Planet Neptune

Neptune photographed by Voyage. Image credit: NASA/JPL — Neptune photographed by Voyager 2. Image credit: NASA/JPL

Neptune is the eight planet from our Sun, one of the four gas giants, and one of the four outer planets in our Solar System. Since the “demotion” of Pluto by the IAU to the status of a dwarf planet – and/or Plutoid and Kuiper Belt Object (KBO) – Neptune is now considered to be the farthest planet in our Solar System.

As one of the planets that cannot be seen with the naked eye, Neptune was not discovered until relatively recently. And given its distance, it has only been observed up close on one occasion – in 1989 by the Voyager 2 spaceprobe. Nevertheless, what we’ve come to know about this gas (and ice) giant in that time has taught us much about the outer Solar System and the history of its formation.

Discovery and Naming:

Neptune’s discovery did not take place until the 19th century, though there are indications that it was observed before long that. For instance, Galileo’s drawings from December 28th, 1612, and January 27th, 1613, contained plotted points which are now known to match up with the positions of Neptune on those dates. However, in both cases, Galileo appeared to have mistaken it for a star.

1821, French astronomer Alexis Bouvard published astronomical tables for the orbit of Uranus. Subsequent observations revealed substantial deviations from the tables, which led Bouvard to hypothesize that an unknown body was perturbing Uranus’ orbit through gravitational interaction.

New Berlin Observatory at Linden Street, where Neptune was discovered observationally. Credit: Leibniz-Institut für Astrophysik Potsdam — *New Berlin Observatory at Linden Street, where Neptune was discovered observationally. Credit: Leibniz-Institute for Astrophysics Potsdam*

In 1843, English astronomer John Couch Adams began work on the orbit of Uranus using the data he had and produced several different estimates in the following years of the planet’s orbit. In 1845–46, Urbain Le Verrier, independently of Adams, developed his own calculations, which he shared with Johann Gottfried Galle of the Berlin Observatory. Galle confirmed the presence of a planet at the coordinates specified by Le Verrier on September 23rd, 1846.

The announcement of the discovery was met with controversy, as both Le Verrier and Adams claimed responsibility. Eventually, an international consensus emerged that both Le Verrier and Adams jointly deserved credit. However, a re-evaluation by historians in 1998 of the relevant historical documents led to the conclusion that Le Verrier was more directly responsible for the discovery and deserves the greater share of the credit.

Claiming the right of discovery, Le Verrier suggested the planet be named after himself, but this met with stiff resistance outside of France. He also suggested the name Neptune, which was gradually accepted by the international community. This was largely because it was consistent with the nomenclature of the other planets, all of which were named after deities from Greco-Roman mythology.

Neptune’s Size, Mass and Orbit:

With a mean radius of 24,622 ± 19 km, Neptune is the fourth largest planet in the Solar System and four times as large as Earth. But with a mass of 1.0243×10²⁶ kg – which is roughly 17 times that of Earth – it is the third most massive, outranking Uranus. The planet has a very minor eccentricity of 0.0086, and orbits the Sun at a distance of 29.81 AU (4.459 x 10⁹ km) at perihelion and 30.33 AU (4.537 x 10⁹ km) at aphelion.

*A size comparison of Neptune and Earth. Credit: NASA*

Neptune takes 16 h 6 min 36 s (0.6713 days) to complete a single sidereal rotation, and 164.8 Earth years to complete a single orbit around the Sun. This means that a single day lasts 67% as long on Neptune, whereas a year is the equivalent of approximately 60,190 Earth days (or 89,666 Neptunian days).

Because Neptune’s axial tilt (28.32°) is similar to that of Earth (~23°) and Mars (~25°), the planet experiences similar seasonal changes. Combined with its long orbital period, this means that the seasons last for forty Earth years. Also owing to its axial tilt being comparable to Earth’s is the fact that the variation in the length of its day over the course of the year is not any more extreme than it on Earth.

Neptune’s orbit also has a profound impact on the region directly beyond it, known as the Kuiper Belt (otherwise known as the “Trans-Neptunian Region”). Much in the same way that Jupiter’s gravity dominates the Asteroid Belt, shaping its structure, so Neptune’s gravity dominates the Kuiper Belt. Over the age of the Solar System, certain regions of the Kuiper belt became destabilised by Neptune’s gravity, creating gaps in the Kuiper belt’s structure.

There also exists orbits within these empty regions where objects can survive for the age of the Solar System. These resonances occur when Neptune’s orbital period is a precise fraction of that of the object – meaning they complete a fraction of an orbit for every orbit made by Neptune. The most heavily populated resonance in the Kuiper belt, with over 200 known objects, is the 2:3 resonance.

Objects in this resonance complete 2 orbits for every 3 of Neptune, and are known as plutinos because the largest of the known Kuiper belt objects, Pluto, is among them. Although Pluto crosses Neptune’s orbit regularly, the 2:3 resonance ensures they can never collide.

Neptune has a number of known trojan objects occupying both the Sun–Neptune L₄ and L₅ Lagrangian Points – regions of gravitational stability leading and trailing Neptune in its orbit. Some Neptune trojans are remarkably stable in their orbits, and are likely to have formed alongside Neptune rather than being captured.

Neptune’s Composition:

Due to its smaller size and higher concentrations of volatiles relative to Jupiter and Saturn, Neptune (much like Uranus) is often referred to as an “ice giant” – a subclass of a giant planet. Also like Uranus, Neptune’s internal structure is differentiated between a rocky core consisting of silicates and metals; a mantle consisting of water, ammonia and methane ices; and an atmosphere consisting of hydrogen, helium and methane gas.

The core of Neptune is composed of iron, nickel and silicates, with an interior model giving it a mass about 1.2 times that of Earth. The pressure at the center is estimated to be 7 Mbar (700 GPa), about twice as high as that at the center of Earth, and with temperatures as high as 5,400 K. At a depth of 7000 km, the conditions may be such that methane decomposes into diamond crystals that rain downwards like hailstones.

The mantle is equivalent to 10 – 15 Earth masses and is rich in water, ammonia and methane. This mixture is referred to as icy even though it is a hot, dense fluid, and is sometimes called a “water-ammonia ocean”. Meanwhile, the atmosphere forms about 5% to 10% of its mass and extends perhaps 10% to 20% of the way towards the core, where it reaches pressures of about 10 GPa – or about 100,000 times that of Earth’s atmosphere.

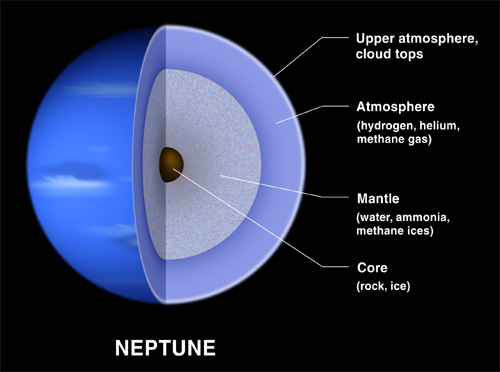
*Composition of Neptune. Image credit: NASA*

Increasing concentrations of methane, ammonia and water are found in the lower regions of the atmosphere. Unlike Uranus, Neptune’s composition has a higher volume of ocean, whereas Uranus has a smaller mantle.

Neptune’s Atmosphere:

At high altitudes, Neptune’s atmosphere is 80% hydrogen and 19% helium, with a trace amount of methane. As with Uranus, this absorption of red light by the atmospheric methane is part of what gives Neptune its blue hue, although Neptune’s is darker and more vivid. Because Neptune’s atmospheric methane content is similar to that of Uranus, some unknown atmospheric constituent is thought to contribute to Neptune’s more intense coloring.

Neptune’s atmosphere is subdivided into two main regions: the lower troposphere (where temperature decreases with altitude), and the stratosphere (where temperature increases with altitude). The boundary between the two, the tropopause, lies at a pressure of 0.1 bars (10 kPa). The stratosphere then gives way to the thermosphere at a pressure lower than 10^-5 to 10^-4 microbars (1 to 10 Pa), which gradually transitions to the exosphere.

Neptune’s spectra suggest that its lower stratosphere is hazy due to condensation of products caused by the interaction of ultraviolet radiation and methane (i.e. photolysis), which produces compounds such as ethane and ethyne. The stratosphere is also home to trace amounts of carbon monoxide and hydrogen cyanide, which are responsible for Neptune’s stratosphere being warmer than that of Uranus.

In this image, the colors and contrasts were modified to emphasize the planet’s atmospheric features. The winds in Neptune’s atmosphere can reach the speed of sound or more. Neptune’s Great Dark Spot stands out as the most prominent feature on the left. Several features, including the fainter Dark Spot 2 and the South Polar Feature, are locked to the planet’s rotation, which allowed Karkoschka to precisely determine how long a day lasts on Neptune. (Image: Erich Karkoschka) — *A modified color/contrast image emphasizing Neptune’s atmospheric features, including wind speed. Credit Erich Karkoschka)*

For reasons that remain obscure, the planet’s thermosphere experiences unusually high temperatures of about 750 K (476.85 °C/890 °F). The planet is too far from the Sun for this heat to be generated by ultraviolet radiation, which means another heating mechanism is involved – which could be the atmosphere’s interaction with ion’s in the planet’s magnetic field, or gravity waves from the planet’s interior that dissipate in the atmosphere.

Because Neptune is not a solid body, its atmosphere undergoes differential rotation. The wide equatorial zone rotates with a period of about 18 hours, which is slower than the 16.1-hour rotation of the planet’s magnetic field. By contrast, the reverse is true for the polar regions where the rotation period is 12 hours.

This differential rotation is the most pronounced of any planet in the Solar System, and results in strong latitudinal wind shear and violent storms. The three most impressive were all spotted in 1989 by the Voyager 2 space probe, and then named based on their appearances.

The first to be spotted was a massive anticyclonic storm measuring 13,000 x 6,600 km and resembling the Great Red Spot of Jupiter. Known as the Great Dark Spot, this storm was not spotted five later (Nov. 2nd, 1994) when the Hubble Space Telescope looked for it. Instead, a new storm that was very similar in appearance was found in the planet’s northern hemisphere, suggesting that these storms have a shorter life span than Jupiter’s.

*Reconstruction of Voyager 2 images showing the Great Black spot (top left), Scooter (middle), and the Small Black Spot (lower right). Credit: NASA/JPL*

The Scooter is another storm, a white cloud group located farther south than the Great Dark Spot. This nickname first arose during the months leading up to the Voyager 2 encounter in 1989, when the cloud group was observed moving at speeds faster than the Great Dark Spot.

The Small Dark Spot, a southern cyclonic storm, was the second-most-intense storm observed during the 1989 encounter. It was initially completely dark; but as Voyager 2 approached the planet, a bright core developed and could be seen in most of the highest-resolution images.

Neptune’s Moons:

Neptune has 14 known satellites, all but one of which are named after Greek and Roman deities of the sea (S/2004 N 1 is currently unnamed). These moons are divided into two groups – the regular and irregular moons – based on their orbit and proximity to Neptune. Neptune’s Regular Moons – Naiad, Thalassa, Despina, Galatea, Larissa, S/2004 N 1, and Proteus – are those that are closest to the planet and which follow circular, prograde orbits that lie in the planet’s equatorial plane.

They range in distance from 48,227 km (Naiad) to 117,646 km (Proteus) from Neptune, and all but the outermost two (S/2004 N 1, and Proteus) orbit Neptune slower than its orbital period of 0.6713 days. Based on observational data and assumed densities, these moons range in size and mass from 96 x 60 x 52 km and 1.9 x 10¹⁷ kg (Naiad) to 436 x 416 x 402 km and 50.35 x 10¹⁷ kg (Proteus).

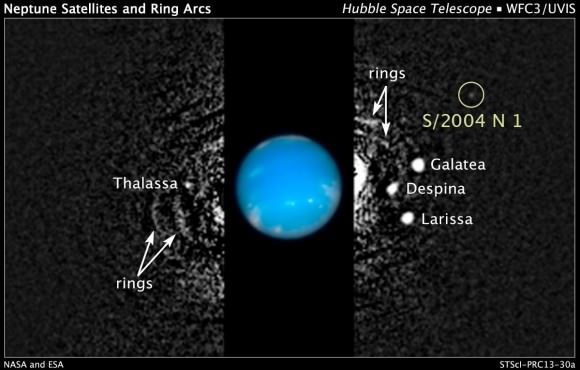
This composite Hubble Space Telescope picture shows the location of a newly discovered moon, designated S/2004 N 1, orbiting the giant planet Neptune, nearly 4.8 billion km (3 billion miles) from Earth. Credit: NASA, ESA, and M. Showalter (SETI Institute).

With the exception of Larissa and Proteus (which are largely rounded) all of Neptune’s inner moons are believed to be elongated in shape. Their spectra also indicates that they are made from water ice contaminated by some very dark material, probably organic compounds. In this respect, the inner Neptunian moons are similar to the inner moons of Uranus.

Neptune’s irregular moons consist of the planet’s remaining satellites (including Triton). They generally follow inclined eccentric and often retrograde orbits far from Neptune. The only exception is Triton, which orbits close to the planet, following a circular orbit, though retrograde and inclined.

In order of their distance from the planet, the irregular moons are Triton, Nereid, Halimede, Sao, Laomedeia, Neso and Psamathe – a group that includes both prograde and retrograde objects. With the exception of Triton and Nereid, Neptune’s irregular moons are similar to those of other giant planets and are believed to have been gravitationally captured by Neptune.

In terms of size and mass, the irregular moons are relatively consistent, ranging from approximately 40 km in diameter and 4 x 10¹⁶kg in mass (Psamathe) to 62 km and 16 x 10¹⁶kg for Halimede. Triton and Nereid are unusual irregular satellites and are thus treated separately from the other five irregular Neptunian moons. Between these two and the other irregular moons, four major differences have been noted.

First of all, they are the largest two known irregular moons in the Solar System. Triton itself is almost an order of magnitude larger than all other known irregular moons and comprises more than 99.5% of all the mass known to orbit Neptune (including the planet’s rings and thirteen other known moons).

*Global Color Mosaic of Triton, taken by Voyager 2 in 1989. Credit: NASA/JPL/USGS*

Secondly, they both have atypically small semi-major axes, with Triton’s being over an order of magnitude smaller than those of all other known irregular moons. Thirdly, they both have unusual orbital eccentricities: Nereid has one of the most eccentric orbits of any known irregular satellite, and Triton’s orbit is a nearly perfect circle. Finally, Nereid also has the lowest inclination of any known irregular satellite

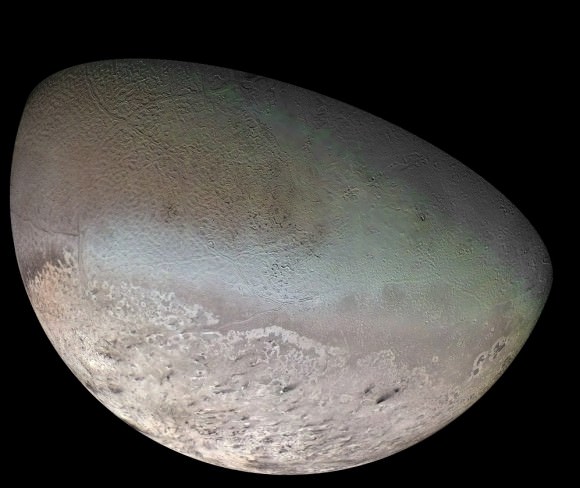
With a mean diameter of around 2700 km and a mass of 214080 ± 520 x 10¹⁷ kg, Triton is the largest of Neptune’s moons, and the only one large enough to achieve hydrostatic equilibrium (i.e. is spherical in shape). At a distance of 354,759 km from Neptune, it also sits between the planet’s inner and outer moons.

Triton follows a retrograde and quasi-circular orbit, and is composed largely of nitrogen, methane, carbon dioxide and water ices. With a geometric albedo of more than 70% and a Bond albedo as high as 90%, it is also one of the brightest objects in the Solar System. The surface has a reddish tint, owning to the interaction of ultraviolet radiation and methane, causing tholins.

Triton is also one of the coldest moons in the Solar System, with surface temperature of about 38 K (-235.2 °C). However, owing to the moon being geologically active (which results in cryovolcanism) and surface temperature variations that cause sublimation, Triton is one of only two moons in the Solar System that has a substantial atmosphere. Much like it’s surface, this atmosphere is composed primarily of nitrogen with small amounts of methane and carbon monoxide, and with an estimated pressure of about 14 nanobar.

Triton has a relatively high density of about 2 g/cm³ indicating that rocks constitute about two thirds of its mass, and ices (mainly water ice) the remaining one third. There also may be a layer of liquid water deep inside Triton, forming a subterranean ocean. Surface features include the large southern polar cap, older cratered planes cross-cut by graben and scarps, as well as youthful features caused by endogenic resurfacing.

Because of its retrograde orbit and relative proximity to Neptune (closer than the Moon is to Earth), Triton is grouped with the planet’s irregular moons (see below). In addition, it is believed to be a captured object, possibly a dwarf planet that was once part of the Kuiper Belt. At the same time, these orbital characteristics are the reason why Triton experiences tidal deceleration. and will eventually spiral inward and collide with the planet in about 3.6 billion years.

Nereid is the third-largest moon of Neptune. It has a prograde but very eccentric orbit and is believed to be a former regular satellite that was scattered to its current orbit through gravitational interactions during Triton’s capture. Water ice has been spectroscopically detected on its surface. Nereid shows large, irregular variations in its visible magnitude, which are probably caused by forced precession or chaotic rotation combined with an elongated shape and bright or dark spots on the surface.

Neptune’s Ring System:

Neptune has five rings, all of which are named after astronomers who made important discoveries about the planet – Galle, Le Verrier, Lassell, Arago, and Adams. The rings are composed of at least 20% dust (with some containing as much as 70%) while the rest of the material consists of small rocks. The planet’s rings are difficult to see because they are dark and vary in density and size.

The Galle ring was named after Johann Gottfried Galle, the first person to see the planet using a telescope; and at 41,000–43,000 km, it is the nearest of Neptune’s rings. The La Verrier ring – which is very narrow at 113 km in width – is named after French astronomer Urbain Le Verrier, the planet’s co-founder.

At a distance of between 53,200 and 57,200 km from Neptune (giving it a width of 4,000 km) the Lassell ring is the widest of Neptune’s rings. This ring is named after William Lassell, the English astronomer who discovered Triton just seventeen days after Neptune was discovered. The Arago ring is 57,200 kilometers from the planet and less than 100 kilometers wide. This ring section is named after Francois Arago, Le Verrier’s mentor and the astronomer who played an active role in the dispute over who deserved credit for discovering Neptune.

The outer Adams ring was named after John Couch Adams, who is credited with the co-discovery of Neptune. Although the ring is narrow at only 35 kilometers wide, it is the most famous of the five due to its arcs. These arcs accord with areas in the ring system where the material of the rings is grouped together in a clump, and are the brightest and most easily observed parts of the ring system.

Although the Adams ring has five arcs, the three most famous are the “Liberty”, “Equality”, and “Fraternity” arcs. Scientists have been traditionally unable to explain the existence of these arcs because, according to the laws of motion, they should distribute the material uniformly throughout the rings. However, stronomers now estimate that the arcs are corralled into their current form by the gravitational effects of Galatea, which sits just inward from the ring.

The rings of Neptune as seen from Voyager 2 during the 1989 flyby. (Credit: NASA/JPL). — *The rings of Neptune as seen from Voyager 2 during the 1989 flyby. Credit: NASA/JPL*

The rings of Neptune are very dark, and probably made of organic compounds that have been altered due to exposition to cosmic radiation. This is similar to the rings of Uranus, but very different to the icy rings around Saturn. They seem to contain a large quantity of micrometer-sized dust, similar in size to the particles in the rings of Jupiter.

It’s believed that the rings of Neptune are relatively young – much younger than the age of the Solar System, and much younger than the age of Uranus’ rings. Consistent with the theory that Triton was a KBO that was seized, by Neptune’s gravity, they are believed to be the result of a collision between some of the planet’s original moons.

Exploration:

The Voyager 2 probe is the only spacecraft to have ever visited Neptune. The spacecraft’s closest approach to the planet occurred on August 25th, 1989, which took place at a distance of 4,800 km (3,000 miles) above Neptune’s north pole. Because this was the last major planet the spacecraft could visit, it was decided to make a close flyby of the moon Triton – similar to what had been done for Voyager 1‘s encounter with Saturn and its moon Titan.

The spacecraft performed a near-encounter with the moon Nereid before it came to within 4,400 km of Neptune’s atmosphere on August 25th, then passed close to the planet’s largest moon Triton later the same day. The spacecraft verified the existence of a magnetic field surrounding the planet and discovered that the field was offset from the center and tilted in a manner similar to the field around Uranus.

Neptune’s rotation period was determined using measurements of radio emissions and Voyager 2 also showed that Neptune had a surprisingly active weather system. Six new moons were discovered during the flyby, and the planet was shown to have more than one ring.

While no missions to Neptune are currently being planned, some hypothetical missions have been suggested. For instance, a possible Flagship Mission has been envisioned by NASA to take place sometime during the late 2020s or early 2030s. Other proposals include a possible Cassini-Huygens-style “Neptune Orbiter with Probes”, which was suggested back in 2003.

Another, more recent proposal by NASA was for Argo – a flyby spacecraft that would be launched in 2019, which would visit Jupiter, Saturn, Neptune, and a Kuiper belt object. The focus would be on Neptune and its largest moon Triton, which would be investigated around 2029.

With its icy-blue color, liquid surface, and wavy weather patterns, Neptune was appropriately named after the Roman god of the sea. And given its distance from our planet, there is still a great deal that remains to be learned about it. In the coming decades, one can only hope that a mission to the outer Solar System and/or Kuiper Belt includes a flyby of Neptune.

We have many interesting articles about Neptune here at Universe Today. Below is a comprehensive list for your viewing (and possibly researching) pleasure!

Characteristics of Neptune:

Position and Movement of Neptune:

Neptune’s Moon and Rings:

History of Neptune:

Neptune’s Surface and Structure:

June 6, 2015May 8, 2017 by Joshua Carroll

Mathematics: The Beautiful Language of the Universe

Let us discuss the very nature of the cosmos. What you may find in this discussion is not what you expect. Going into a conversation about the universe as a whole, you would imagine a story full of wondrous events such as stellar collapse, galactic collisions, strange occurrences with particles, and even cataclysmic eruptions of energy. You may be expecting a story stretching the breadth of time as we understand it, starting from the Big Bang and landing you here, your eyes soaking in the photons being emitted from your screen. Of course, the story is grand. But there is an additional side to this amazing assortment of events that oftentimes is overlooked; that is until you truly attempt to understand what is going on. Behind all of those fantastic realizations, there is a mechanism at work that allows for us to discover all that you enjoy learning about. That mechanism is mathematics, and without it the universe would still be shrouded in darkness. In this article, I will attempt to persuade you that math isn’t some arbitrary and sometimes pointless mental task that society makes it out to be, and instead show you that it is a language we use to communicate with the stars.

We are currently bound to our solar system. This statement is actually better than it sounds, as being bound to our solar system is one major step up from being bound simply to our planet, as we were

A defining moment for humanity: Galileo turing his spyglass towards the sky

before some very important minds elected to turn their geniuses toward the heavens. Before those like Galileo, who aimed his spyglass towards the sky, or Kepler discovering that planets move about the sun in ellipses, or Newton discovering a gravitational constant, mathematics was somewhat limited, and our understanding of the universe rather ignorant. At its core, mathematics allows a species bound to its solar system to probe the depths of the cosmos from behind a desk. Now, in order to appreciate the wonder that is mathematics, we must first step back and briefly look at its beginnings and how it is integrally tied into our very existence.

Mathematics almost certainly came about from very early human tribes (predating Babylonian culture which is attributed to some of the first organized mathematics in recorded history), that may have used math as a way of keeping track of lunar or solar cycles, and keeping count of animals, food and/or people by leaders. It is as natural as when you are a young child and you can see that you have

Ancient Babylonian tablet displaying early mathematics

one toy plus one other toy, meaning you have more than one toy. As you get older, you develop the ability to see that 1+1=2, and thus simple arithmetic seems to be interwoven into our very nature. Those that profess that they don’t have a mind for math are sadly mistaken because just as we all have a mind for breathing, or blinking, we all have this innate ability to understand arithmetic. Mathematics is both a natural occurrence and a human designed system. It would appear that nature grants us this ability to recognize patterns in the form of arithmetic, and then we systematically construct more complex mathematical systems that aren’t obvious in nature but let us further communicate with nature.

All this aside, mathematics developed alongside of human development, and carried on similarly with each culture that was developing it simultaneously. It’s a wonderful observation to see that cultures that had no contact with one another were developing similar mathematical constructs without conversing. However, it wasn’t until mankind decidedly turned their mathematical wonder towards the sky that math truly began to develop in an astonishing way. It is by no mere coincidence that our scientific revolution was spurred by the development of more advanced mathematics built not to tally sheep or people, but rather to further our understandings of our place within the universe. Once Galileo began measuring the rates at which objects fell in an attempt to show mathematically that the mass of an object had little to do with the speed in which it fell, mankind’s future would forever be altered.

This is where the cosmic perspective ties in to our want to further our mathematical knowledge. If it were not for math, we would still think we were on one of a few planets orbiting a star amidst the backdrop of seemingly motionless lights. This is a rather bleak outlook today compared to what we now know

Johannes Kepler used mathematics to model his observations of the planets.

about the awesomely large universe we reside in. This idea of the universe motivating us to understand more about mathematics can be inscribed in how Johannes Kepler used what he observed the planets doing, and then applied mathematics to it to develop a fairly accurate model (and method for predicting planetary motion) of the solar system. This is one of many demonstrations that illustrate the importance of mathematics within our history, especially within astronomy and physics.

The story of mathematics becomes even more amazing as we push forward to one of the most advanced thinkers humanity has ever known. Sir Isaac Newton, when pondering the motions of Halley’s Comet, came to the realization that the math that had been used thus far to describe physical motion of massive

bodies, simply would not suffice if we were to ever understand anything beyond that of our seemingly limited celestial nook. In a show of pure brilliance that lends validity to my earlier statement about how we can take what we naturally have and then construct a more complex system upon it, Newton developed the Calculus in which this way of approaching moving bodies, he was able to accurately model the motion of not only Halley’s comet, but also any other heavenly body that moved across the sky.

In one instant, our entire universe opened up before us, unlocking almost unlimited abilities for us to converse with the cosmos as never before. Newton also expanded upon what Kepler started. Newton recognized that Kepler’s mathematical equation for planetary motion, Kepler’s 3rd Law ( P²=A³ ), was purely based on empirical observation, and was only meant to measure what we observed within our solar system. Newton’s mathematical brilliance was in realizing that this basic equation could be made universal by applying a gravitational constant to the equation, in which gave birth to perhaps one of the most important equations to ever be derived by mankind; Newton’s Version of Kepler’s Third Law.

You can still see where Kepler's 3rd Law remains, but with the added values of the gravitational constant G, and M and m representing the masses of the two bodies in question, this equation is no longer restricted to just our solar system — You can still see where Kepler’s 3rd Law remains, but with the added values of the gravitational constant G, and M and m representing the masses of the two bodies in question, this equation is no longer restricted to just our solar system

What Newton realized was that when things move in non-linear ways, using basic Algebra would not produce the correct answer. Herein lays one of the main differences between Algebra and Calculus. Algebra allows one to find the slope (rate of change) of straight lines (constant rate of change), whereas Calculus allows one to find the slope of curved lines (variable rate of change). There are obviously many more applications of Calculus than just this, but I am merely illustrating a fundamental difference between the two in order to show you just how revolutionary this new concept was. All at once, the motions of planets and other objects that orbit the sun became more accurately measurable, and thus we gained the ability to understand the universe a little deeper. Referring back to Netwon’s Version of Kepler’s Third Law, we were now able to apply (and still do) this incredible physics equation to almost anything that is orbiting something else. From this equation, we can determine the mass of either of the objects, the distance apart they are from each other, the force of gravity that is exerted between the two, and other physical qualities built from these simple calculations.

With his understanding of mathematics, Newton was able to derive the aforementioned gravitational constant for all objects in the universe ( G = 6.672×10^-11 N m² kg^-2 ). This constant allowed him to unify astronomy and physics which then permitted predictions about how things moved in the universe. We could now measure the masses of planets (and the sun) more accurately, simply according to Newtonian physics (aptly named to honor just how important Newton was within physics and mathematics). We could now apply this newfound language to the cosmos, and begin coercing it to divulge its secrets. This was a defining moment for humanity, in that all of those things that prohibited our understandings prior to this new form of math were now at our fingertips, ready to be discovered. This is the brilliance of understanding Calculus, in that you are speaking the language of the stars.

There perhaps is no better illustration of the power that mathematics awarded us then in the discovery of the planet Neptune. Up until its discovery in September of 1846, planets were discovered simply by observing certain “stars” that were moving against the backdrop of all the other stars in odd ways. The term planet is Greek for “wanderer”, in that these peculiar stars wandered across the sky in noticeable patterns at different times of the year. Once the telescope was first turned upwards towards the sky by Galileo, these wanderers resolved into other worlds that appeared to be like ours. If fact, some of these worlds appeared to be little solar systems themselves, as Galileo discovered when he began recording the moons of Jupiter as they orbited around it.

After Newton presented his physics equations to the world, mathematicians were ready and excited to begin applying them to what we had been keeping track of for years. It was as if we were thirsty for the knowledge, and finally someone turned on the faucet. We began measuring the motions of the planets and gaining more accurate models for how they behaved. We used these equations to approximate the mass of the Sun. We were able to make remarkable predictions that were validated time and again simply by observation. What we were doing was unprecedented, as we were using mathematics to make almost impossible to know predictions that you would think we could never make without actually going to these planets, and then using actual observation to prove the math correct. However, what we also did was begin to figure out some odd discrepancies with certain things. Uranus, for instance, was behaving not as it should according to Newton’s laws.

Here you can see that the inner planet is being perturbed by the outer planet, in our situation, that outer planet was Neptune, not yet discovered. — Here you can see that the inner planet is being perturbed by the outer planet. In our situation, that outer planet was Neptune, which had yet to be discovered.

What makes the discovery of Neptune so wonderful was the manner in which it was discovered. What Newton had done was uncover a deeper language of the cosmos, in which the universe was able to reveal more to us. And this is exactly what happened when we applied this language to the orbit of Uranus. The manner in which Uranus orbited was curious and did not fit what it should have if it was the only planet that far out from the sun. Looking at the numbers, there had to be something else out there perturbing its orbit. Now, before Newton’s mathematical insights and laws, we would have had no reason to suspect anything was wrong in what we observed. Uranus orbited in the way Uranus orbited; it was just how it was. But, again revisiting that notion of mathematics being an ever increasing dialogue with the universe, once we asked the question in the right format, we realized that there really must be something else beyond what we couldn’t see. This is the beauty of mathematics writ large; an ongoing conversation with the universe in which more than we may expect is revealed.

It came to a French mathematician Urbain Le Verrier who sat down and painstakingly worked through the mathematical equations of the orbit of Uranus. What he was doing was using Newton’s mathematical equations backwards, realizing that there must be an object out there beyond the orbit of Uranus that was also orbiting the sun,

French mathematician who discovered the planet Neptune by using only mathematics

and then looking to apply the right mass and distance that this unseen object required for perturbing the orbit of Uranus in the way we were observing it was. This was phenomenal, as we were using parchment and ink to find a planet that nobody had ever actually observed. What he found was that an object, soon to be Neptune, had to be orbiting at a specific distance from the sun, with the specific mass that would cause the irregularities in the orbital path of Uranus. Confident of his mathematical calculations, he took his numbers to the New Berlin Observatory, where the astronomer Johann Gottfried Galle looked exactly where Verrier’s calculations told him to look, and there lay the 8th and final planet of our solar system, less than 1 degree off from where Verrier’s calculations said for him to look. What had just happened was an incredible confirmation of Newton’s gravitational theory and proved that his mathematics were correct.

Are There Oceans on Neptune — Neptune is more than just the 8th planet in our solar system; it is a celestial reminder of the power that mathematics grants us.

These types of mathematical insights continued on long after Newton. Eventually, we began to learn much more about the universe with the advent of better technology (brought about by advances in mathematics). As we moved into the 20th century, quantum theory began to take shape, and we soon realized that Newtonian physics and mathematics seemed to hold no sway over what we observed on the quantum level. In another momentous event in human history, yet again brought forth by the advancement in mathematics, Albert Einstein unveiled his theories of General and Special Relativity, which was a new way to look not only at gravity, but

Einstein's Relativity, yet another momentous advancement for humanity brought forth from an ongoing mathematical dialogue. Image via Pixabay. — Einstein’s equation for the energy-mass equivalency, yet another incredible advancement for humanity brought forth from an ongoing mathematical dialogue. Image via Pixabay.

also on energy and the universe in general. What Einstein’s mathematics did was allow for us to yet again uncover an even deeper dialogue with the universe, in which we began to understand its origins.

Continuing this trend of advancing our understandings, what we have realized is that now there are two sects of physics that do not entirely align. Newtonian or “classical” physics, that works extraordinarily well with the very large (motions of planets, galaxies, etc…) and quantum physics that explains the extremely small (the interactions of sub-atomic particles, light, etc…). Currently, these two areas of physics are not in alignment, much like two different dialects of a language. They are similar and they both work, but they are not easily reconcilable with one another. One of the greatest challenges we face today is attempting to create a mathematical grand “theory of everything” which either unites the laws in the quantum world with that of the macroscopic world, or to work to explain everything solely in terms of quantum mechanics. This is no easy task, but we are striving forward nonetheless.

As you can see, mathematics is more than just a set of vague equations and complex rules that you are required to memorize. Mathematics is the language of the universe, and in learning this language, you are opening yourself up the core mechanisms by which the cosmos operates. It is the same as traveling to a new land, and slowly picking up on the native language so that you may begin to learn from them. This mathematical endeavor is what allows us, a species bound to our solar system, to explore the depths of the universe. As of now, there simply is no way for us to travel to the center of our galaxy and observe the supermassive black hole there to visually confirm its existence. There is no way for us to venture out into a Dark Nebula and watch in real time a star being born. Yet, through mathematics, we are able to understand how these things exist and work. When you set about to learn math, you are not only expanding your mind, but you are connecting with the universe on a fundamental level. You can, from your desk, explore the awesome physics at the event horizon of a black hole, or bear witness to the destructive fury behind a supernova. All of those things that I mentioned at the beginning of this article come into focus through mathematics. The grand story of the universe is written in mathematics, and our ability to translate those numbers into the events that we all love to learn about is nothing short of amazing. So remember, when you are presented with the opportunity to learn math, accept every bit of it because math connects us to the stars.