The spring is a marvel of human engineering and creativity. For one, it comes in so many varieties – the compression spring, the extension spring, the torsion spring, the coil spring, etc. – all of which serve different and specific functions. These functions in turn allow for the creation of many man-made objects, most of which emerged as part of the Scientific Revolution during the late 17th and 18th centuries.
As an elastic object used to store mechanical energy, the applications for them are extensive, making possible such things as an automotive suspension systems, pendulum clocks, hand sheers, wind-up toys, watches, rat traps, digital micromirror devices, and of course, the Slinky.
Like so many other devices invented over the centuries, a basic understanding of the mechanics is required before it can so widely used. In terms of springs, this means understanding the laws of elasticity, torsion and force that come into play – which together are known as Hooke’s Law.
Hooke’s Law is a principle of physics that states that the that the force needed to extend or compress a spring by some distance is proportional to that distance. The law is named after 17th century British physicist Robert Hooke, who sought to demonstrate the relationship between the forces applied to a spring and its elasticity.

He first stated the law in 1660 as a Latin anagram, and then published the solution in 1678 as ut tensio, sic vis – which translated, means “as the extension, so the force” or “the extension is proportional to the force”).
This can be expressed mathematically as F= -kX, where F is the force applied to the spring (either in the form of strain or stress); X is the displacement of the spring, with a negative value demonstrating that the displacement of the spring once it is stretched; and k is the spring constant and details just how stiff it is.
Hooke’s law is the first classical example of an explanation of elasticity – which is the property of an object or material which causes it to be restored to its original shape after distortion. This ability to return to a normal shape after experiencing distortion can be referred to as a “restoring force”. Understood in terms of Hooke’s Law, this restoring force is generally proportional to the amount of “stretch” experienced.
In addition to governing the behavior of springs, Hooke’s Law also applies in many other situations where an elastic body is deformed. These can include anything from inflating a balloon and pulling on a rubber band to measuring the amount of wind force is needed to make a tall building bend and sway.
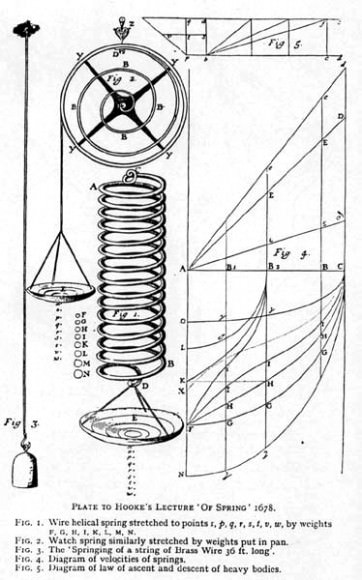
This law has had many important practical applications, with one being the creation of a balance wheel, which made possible the creation of the mechanical clock, the portable timepiece, the spring scale and the manometer (aka. the pressure gauge). Also, because it is a close approximation of all solid bodies (as long as the forces of deformation are small enough), numerous branches of science and engineering as also indebted to Hooke for coming up with this law. These include the disciplines of seismology, molecular mechanics and acoustics.
However, like most classical mechanics, Hooke’s Law only works within a limited frame of reference. Because no material can be compressed beyond a certain minimum size (or stretched beyond a maximum size) without some permanent deformation or change of state, it only applies so long as a limited amount of force or deformation is involved. In fact, many materials will noticeably deviate from Hooke’s law well before those elastic limits are reached.
Still, in its general form, Hooke’s Law is compatible with Newton’s laws of static equilibrium. Together, they make it possible to deduce the relationship between strain and stress for complex objects in terms of the intrinsic materials of the properties it is made of. For example, one can deduce that a homogeneous rod with uniform cross section will behave like a simple spring when stretched, with a stiffness (k) directly proportional to its cross-section area and inversely proportional to its length.

Another interesting thing about Hooke’s law is that it is a a perfect example of the First Law of Thermodynamics. Any spring when compressed or extended almost perfectly conserves the energy applied to it. The only energy lost is due to natural friction.
In addition, Hooke’s law contains within it a wave-like periodic function. A spring released from a deformed position will return to its original position with proportional force repeatedly in a periodic function. The wavelength and frequency of the motion can also be observed and calculated.
The modern theory of elasticity is a generalized variation on Hooke’s law, which states that the strain/deformation of an elastic object or material is proportional to the stress applied to it. However, since general stresses and strains may have multiple independent components, the “proportionality factor” may no longer be just a single real number.
A good example of this would be when dealing with wind, where the stress applied varies in intensity and direction. In cases like these, it is best to employ a linear map (aka. a tensor) that can be represented by a matrix of real numbers instead of a single value.
If you enjoyed this article there are several others that you will enjoy on Universe Today. Here is one about Sir Isaac Newton’s contributions to the many fields of science. Here is an interesting article about gravity.
There are also some great resources online, such as this lecture on Hooke’s Law that you can watch on academicearth.org. There is also a great explanation of elasticity on howstuffworks.com.
You can also listen to Episode 138, Quantum Mechanics from Astronomy Cast for more information.
Sources:
Hyperphysics
Physics 24/7

