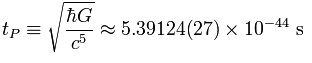We’ve come a long way in 13.8 billion years; but despite our impressively extensive understanding of the Universe, there are still a few strings left untied. For one, there is the oft-cited disconnect between general relativity, the physics of the very large, and quantum mechanics, the physics of the very small. Then there is problematic fate of a particle’s intrinsic information after it falls into a black hole. Now, a new interpretation of fundamental physics attempts to solve both of these conundrums by making a daring claim: at certain scales, space and time simply do not exist.
Let’s start with something that is not in question. Thanks to Einstein’s theory of special relativity, we can all agree that the speed of light is constant for all observers. We can also agree that, if you’re not a photon, approaching light speed comes with some pretty funky rules – namely, anyone watching you will see your length compress and your watch slow down.
But the slowing of time also occurs near gravitationally potent objects, which are described by general relativity. So if you happen to be sight-seeing in the center of the Milky Way and you make the regrettable decision to get too close to our supermassive black hole’s event horizon (more sinisterly known as its point-of-no-return), anyone observing you will also see your watch slow down. In fact, he or she will witness your motion toward the event horizon slow dramatically over an infinite amount of time; that is, from your now-traumatized friend’s perspective, you never actually cross the event horizon. You, however, will feel no difference in the progression of time as you fall past this invisible barrier, soon to be spaghettified by the black hole’s immense gravity.
So, who is “correct”? Relativity dictates that each observer’s point of view is equally valid; but in this situation, you can’t both be right. Do you face your demise in the heart of a black hole, or don’t you? (Note: This isn’t strictly a paradox, but intuitively, it feels a little sticky.)
And there is an additional, bigger problem. A black hole’s event horizon is thought to give rise to Hawking radiation, a kind of escaping energy that will eventually lead to both the evaporation of the black hole and the destruction of all of the matter and energy that was once held inside of it. This concept has black hole physicists scratching their heads. Because according to the laws of physics, all of the intrinsic information about a particle or system (namely, the quantum wavefunction) must be conserved. It cannot just disappear.

Why all of these bizarre paradoxes? Because black holes exist in the nebulous space where a singularity meets general relativity – fertile, yet untapped ground for the elusive theory of everything.
Enter two interesting, yet controversial concepts: doubly special relativity and gravity’s rainbow.
Just as the speed of light is a universally agreed-upon constant in special relativity, so is the Planck energy in doubly special relativity (DSR). In DSR, this value (1.22 x 1019 GeV) is the maximum energy (and thus, the maximum mass) that a particle can have in our Universe.
Two important consequences of DSR’s maximum energy value are minimum units of time and space. That is, regardless of whether you are moving or stationary, in empty space or near a black hole, you will agree that classical space breaks down at distances shorter than the Planck length (1.6 x 10-35 m) and classical time breaks down at moments briefer than the Planck time (5.4 x 10-44 sec).
In other words, spacetime is discrete. It exists in indivisible (albeit vanishingly small) units. Quantum below, classical above. Add general relativity into the picture, and you get the theory of gravity’s rainbow.
Physicists Ahmed Farag Ali, Mir Faizal, and Barun Majumder believe that these theories can be used to explain away the aforementioned black hole conundrums – both your controversial spaghettification and the information paradox. How? According to DSR and gravity’s rainbow, in regions smaller than 1.6 x 10-35 m and at times shorter than 5.4 x 10-44 sec… the Universe as we know it simply does not exist.
“In gravity’s rainbow, space does not exist below a certain minimum length, and time does not exist below a certain minimum time interval,” explained Ali, who, along with Faizal and Majumder, authored a paper on this topic that was published last month. “So, all objects existing in space and occurring at a time do not exist below that length and time interval [which are associated with the Planck scale].”
Luckily for us, every particle we know of, and thus every particle we are made of, is much larger than the Planck length and endures for much longer than the Planck time. So – phew! – you and I and everything we see and know can go on existing. (Just don’t probe too deeply.)
The event horizon of a black hole, however, is a different story. After all, the event horizon isn’t made of particles. It is pure spacetime. And according to Ali and his colleagues, if you could observe it on extremely short time or distance scales, it would cease to have meaning. It wouldn’t be a point-of-no-return at all. In their view, the paradox only arises when you treat spacetime as continuous – without minimum units of length and time.
“As the information paradox depends on the existence of the event horizon, and an event horizon like all objects does not exist below a certain length and time interval, then there is no absolute information paradox in gravity’s rainbow. The absence of an effective horizon means that there is nothing absolutely stopping information from going out of the black hole,” concluded Ali.
No absolute event horizon, no information paradox.
And what of your spaghettification within the black hole? Again, it depends on the scale at which you choose to analyze your situation. In gravity’s rainbow, spacetime is discrete; therefore, the mathematics reveal that both you (the doomed in-faller) and your observer will witness your demise within a finite length of time. But in the current formulation of general relativity, where spacetime is described as continuous, the paradox arises. The in-faller, well, falls in; meanwhile, the observer never sees the in-faller pass the event horizon.
“The most important lesson from this paper is that space and time exist only beyond a certain scale,” said Ali. “There is no space and time below that scale. Hence, it is meaningless to define particles, matter, or any object, including black holes, that exist in space and time below that scale. Thus, as long as we keep ourselves confined to the scales at which both space and time exist, we get sensible physical answers. However, when we try to ask questions at length and time intervals that are below the scales at which space and time exist, we end up getting paradoxes and problems.”
To recap: if spacetime continues on arbitrarily small scales, the paradoxes remain. If, however, gravity’s rainbow is correct and the Planck length and the Planck time are the smallest unit of space and time that fundamentally exist, we’re in the clear… at least, mathematically speaking. Unfortunately, the Planck scales are far too tiny for our measly modern particle colliders to probe. So, at least for now, this work provides yet another purely theoretical result.
The paper was published in the January 23 issue of Europhysics Letters. A pre-print of the paper is available here.