If nothing else catches your attention in the title then surely ‘hypernebula’ does! There are some amazing processes scattered around the cosmos, of particular interest are the fast radio bursts (FRB). These brief flashes of radiation happen without warning…until now. A team in the Netherlands have identified a second FRB as coming from within a hyper nebula – a dense and highly magnetised cloud of plasma that is illuminated by a powerful but unknown source!
Artist rendition of a radio telescope discovering ultra-fast radio bursts that were recently discovered and the focus of this recent study. (Credit: Daniëlle Futselaar/www.artsource.nl)
A recent study published in Nature Astronomy examines the discovery of what astronomers are dubbing “ultra-fast radio bursts”, a new type of fast radio bursts (FRBs) that the team determined lasts for a mind-boggling ten millionths of a second or less. Traditionally, FRBs have been found to last only thousandths of a second, but this study builds on a 2021 study that hypothesized FRBs could possibly last for millionths of a second. This also comes after astronomers recently announced the discovery of the oldest and farthest FRB ever observed, approximately 8 billion light-years from Earth.
A cluster of ancient stars (left) close to the spiral galaxy Messier 81 (M81) is the source of extraordinarily bright and short radio signals. The image shows in blue-white a graph of how one flash’s brightness changed over the course of only tens of microseconds.
(Image credit: ASTRON/Daniëlle Futselaar, artsource.nl)
Fast Radio Bursts (FRBs) are among the top mysteries facing astronomers today. First discovered in 2007 (the famous “Lorimer Burst“), these energetic events consist of huge bursts of radio waves that typically last mere milliseconds. While most events observed to date have been one-off events, astronomers have detected a few FRBs that were repeating in nature. The cause of these bursts remains unknown, with theories ranging from rotating neutron stars and magnetars to extraterrestrials!
Since the first event was detected fifteen years ago, improvements in our instruments and dedicated arrays have led to many more detections! In another milestone, an international team of astronomers recently made high-precision measurements of a repeating FRB located in the spiral galaxy Messier 81 (M81)- the closest FRB observed to date. The team’s findings have helped resolve some questions about this mysterious phenomenon while raising others.
The CHIME Telescope, located at the Dominion Radio Astrophysical Observatory (DRAO), in British Columbia. Credit: chime-experiment.ca
Since they were first detected in 2007, Fast Radio Bursts (FRBs) have been a source of mystery to astronomers. In radio astronomy, this phenomenon refers to transient radio pulses coming from distant sources that typically last a few milliseconds on average. Despite the detection of dozens of events since 2007, scientists are still not sure what causes them – though theories range from exploding stars, black holes, and magnetars to alien civilizations!
To shed light on this mysterious phenomena, astronomers are looking to new instruments to help search for and study FRBs. One of these is the Canadian Hydrogen Intensity Mapping Experiment (CHIME), a revolutionary new radio telescope located at the Dominion Radio Astrophysical Observatory (DRAO) in British Columbia. On July 25th, still in its first year, this telescope made its first-ever detection, an event known as FRB 180725A.
The detection of FRB 180725A was announced online in a “Astronomer’s Telegram” post, which is intended to alert the astronomical community about possible new finds and encourage follow-up observations. The detection of FRB 180725A is very preliminary at this point, and more research is needed before its existence as an FRB can be confirmed.
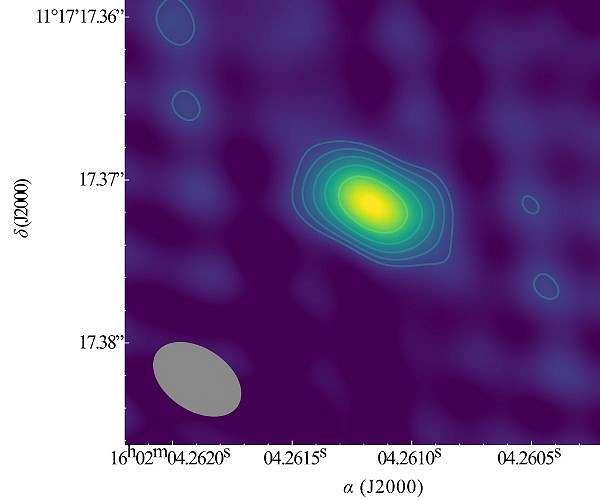
As they stated in the Astronomers Telegram announcement, the radio was signal was detected on July 25th, at precisely 17:59:43.115 UTC (09:59.43.115 PST), and at a radio frequency of 400 MHz:
“The automated pipeline triggered the recording to disk of ~20 seconds of buffered raw intensity data around the time of the FRB. The event had an approximate width of 2 ms and was found at dispersion measure 716.6 pc/cm^3 with a signal-to-noise ratio S/N ~20.6 in one beam and 19.4 in a neighboring beam. The centers of these, approximately 0.5 deg wide and circular beams, were at RA, Dec = (06:13:54.7, +67:04:00.1; J2000) and RA, Dec = (06:12:53.1, +67:03:59.1; J2000).”
Research into Fast Radio Bursts is still in its infancy, being a little more than a decade old. The first ever to be detected was the famous Lorimer Burst, which was named after it discoverer – Duncan Lorimer, from West Virginia University. This burst lasted a mere five milliseconds and appeared to be coming from a location near the Large Magellanic Cloud, billions of light years away.
So far, the only FRB that has been found to be repeating was the mysterious signal known as FRB 121102, which was detected by the Arecibo radio telescope in Puerto Rico in 2012. The nature of this FRB was first noticed by a team of students from McGill University (led by then-PhD Student Paul Scholz), who sifted through the Arecibo data and determined that the initial burst was followed by 10 additional burst consistent with the original signal.
The NSF’s Arecibo Observatory, which is located in Puerto Rico, is the world largest radio telescope. Arecibo detected 11 FRBs over the course of 2 months. Credit: NAIC
In addition to being the first time that this Canadian facility detected a possible FRB coming from space, this is the first time that an FRB has been detected below the 700 MHz range. However, as the CHIME team indicate in their announcement, other signals of equal intensity may have occurred in the past, which were simply not recognized as FRBs at the time.
“Additional FRBs have been found since FRB 180725A and some have flux at frequencies as low as 400 MHz,” they wrote. “These events have occurred during both the day and night and their arrival times are not correlated with known on-site activities or other known sources of terrestrial RFI (Radio Frequency Identification).”
As a result, this most-recent detection (if confirmed) could help astronomers shed some additional light on what causes FRBs, not to mention place some constraints on what frequencies they can occur at. Much like the study of gravitational waves, the field of study is new but rapidly growing, and made possible by the addition of cutting-edge instruments and facilities around the world.
The Parkes Telescope in New South Wales, Australia. Credit: Roger Ressmeyer/Corbis
Fast Radio Bursts (FRBs) have been one of the more puzzling and fascinating areas of astronomical study ever since the first was detected in 2007 (known as the Lorimer Burst). Much like gravitational waves, the study of these short-lived radio pulses (which last only a few milliseconds) is still in its infancy, and only a 33 events have been detected. What’s more, scientists are still not sure what accounts for them.
While some believe that they are entirely natural in origin, others have speculated that they could be evidence of extra-terrestrial activity. Regardless of their cause, according to a recent study, three FRBs were detected this month in Australia by the Parkes Observatory radio telescope in remote Australia. Of these three, one happened to be the most powerful FRB recorded to date.
The signals were detected on March 1st, March 9th, and March 11th, and were designated as FRB 180301, FRB 180309 and FRB 180311. Of these, the one recorded on March 9th (FRB 180309) was the brightest ever recorded, having a signal-to-noise ratio that was four times higher than the previous brightest FRB. This event, known as FRB 170827, was detected on August 27th, 2017, by the UTMOST array in Australia.
The Parkes radio telescope, one of the telescopes comprising CSIRO’s Australia Telescope National Facility. Credit: CSIRO
All three of these events were detected by the Parkes radio telescope, which is located in New South Wales about 380 kilometers (236 mi) from Sydney. As one of three telescopes that makes up the Australia Telescope National Facility, this telescope has been studying pulsars, rapidly spinning neutron stars, and conducting large-scale surveys of the sky since 1961. In recent years, it has been dedicated to the detection of FRBs in our Universe.
Considering how rare and short-lived FRBs are, recording three in the space of one month is quite the achievement. What’s more, the fact that the detections happened in real-time, rather than being discovered in archival data, is also impressive. Shortly after the event, Stefan Oslowski (of the Swinburne University of Technology) tweeted about this rather fortunate discovery (see below).
At present, none of the three events are believed to be “repeaters” – aka. Repeating Fast Radio Bursts. So far, only one FRB has been found to be repeating. This was none other than FRB 121102, which was first detected by the Arecibo radio telescope in Puerto Rico on November 2nd, 2012. In 2015, several more bursts were detected from this some source which had properties that were consistent with the original signal.
As noted, and in spite of all the events that have been detected, scientists are still not sure what causes these strange bursts. But with three more events detected, and the possibility that they could repeat in the near-future, scientists now have more events to pore over and base their theories on. And with next-generation arrays being constructed, a great many more events (and repeaters) are likely to be detected in the coming years.
An artist's impression of the cosmic web, the filamentary structure that fills the entire Universe. Credit: M. Weiss/CfA
When astronomers first noted the detection of a Fast Radio Burst (FRB) in 2007 (aka. the Lorimer Burst), they were both astounded and intrigued. This high-energy burst of radio pulses, which lasted only a few milliseconds, appeared to be coming from outside of our galaxy. Since that time, astronomers have found evidence of many FRBs in previously-recorded data, and are still speculating as to what causes them.
Thanks to subsequent discoveries and research, astronomers now know that FRBs are far more common than previously thought. In fact, according to a new study by a team of researchers from the Harvard-Smithsonian Center for Astrophysics (CfA), FRBs may occur once every second within the observable Universe. If true, FRBs could be a powerful tool for researching the origins and evolution of the cosmos.
As noted, FRBs have remained something of a mystery since they were first discovered. Not only do their causes remain unknown, but much about their true nature is still not understood. As Dr. Fialkov told Universe Today via email:
“FRBs (or fast radio bursts) are astrophysical signals of an undetermined nature. The observed bursts are short (or millisecond duration), bright pulses in the radio part of the electromagnetic spectrum (at GHz frequencies). Only 24 bursts have been observed so far and we still do not know for sure which physical processes trigger them. The most plausible explanation is that they are launched by rotating magnetized neutron stars. However, this theory is to be confirmed.”
For the sake of their study, Fialkov and Loeb relied on observations made by multiple telescopes of the repeating fast radio burst known as FRB 121102. This FRB was first observed in 2012 by researchers using the Arecibo radio telescope in Puerto Rico, and has since been confirmed to be coming from a galaxy located 3 billion light years away in the direction of the Auriga constellation.
Since it was discovered, additional bursts have been detected coming from its location, making FRB 121102 the only known example of a repeating FRB. This repetitive nature has also allowed astronomers to conduct more detailed studies of it than any other FRB. As Prof. Loeb told Universe Today via email, these and other reasons made it an ideal target for their study:
“FRB 121102 is the only FRB for which a host galaxy and a distance were identified. It is also the only repeating FRB source from which we detected hundreds of FRBs by now. The radio spectrum of its FRBs is centered on a characteristic frequency and not covering a very broad band. This has important implications for the detectability of such FRBs, because in order to find them the radio observatory needs to be tuned to their frequency.”
Image of the sky where the radio burst FRB 121102 was found, in the constellation Auriga. You can see its location with a green circle. At left is supernova remnant S147 and at right, a star formation area called IC 410. Credit: Rogelio Bernal Andreo (DeepSkyColors.com)
Based on what is known about FRB 121102, Fialkov and Loeb conducted a series of calculations that assumed that it’s behavior was representative of all FRBs. They then projected how many FRBs would exist across the entire sky and determined that within the observable Universe, a FRB would likely be taking place once every second. As Dr. Fialkov explained:
“Assuming that FRBs are produced by galaxies of a particular type (e.g., similar to FRB 121102) we can calculate how many FRBs have to be produced by each galaxy to explain the existing observations (i.e., 2000 per sky per day). With this number in mind we can infer the production rate for the entire population of galaxies. This calculation shows that an FRB occurs every second when accounting for all the faint events.”
While the exact nature and origins of FRBs are still unknown – suggestions include rotating neutron stars and even alien intelligence! – Fialkov and Loeb indicate that they could be used to study the structure and evolution of the Universe. If indeed they occur with such regular frequency throughout the cosmos, then more distant sources could act as probes which astronomers would then rely on to plumb the depths of space.
For instance, over vast cosmic distances, there is a significant amount of intervening material that makes it difficult for astronomers to study the Cosmic Microwave Background (CMB) – the leftover radiation from the Big Bang. Studies of this intervening material could lead to a new estimates of just how dense space is – i.e. how much of it is composed of ordinary matter, dark matter, and dark energy – and how rapidly it is expanding.
Gemini composite image of the field around FRB 121102, the only repeating FRB discovered so far. Credit: Gemini Observatory/AURA/NSF/NRC
And as Prof. Loeb indicated, FRBs could also be used to explore enduring cosmlogical questions, like how the “Dark Age” of the Universe ended:
“FRBs can be used to measure the column of free electrons towards their source. This can be used to measure the density of ordinary matter between galaxies in the present-day universe. In addition, FRBs at early cosmic times can be used to find out when the ultraviolet light from the first stars broke up the primordial atoms of hydrogen left over from the Big Bang into their constituent electrons and protons.”
The “Dark Age”, which occurred between 380,000 and 150 million years after the Big Bang, was characterized by a “fog” of hydrogen atoms interacting with photons. As a result of this, the radiation of this period is undetectable by our current instruments. At present, scientists are still attempting to resolve how the Universe made the transition between these “Dark Ages” and subsequent epochs when the Universe was filled with light.
This period of “reionization”, which took place 150 million to 1 billion years after the Big Bang, was when the first stars and quasars formed. It is generally believed that UV light from the first stars in the Universe traveled outwards to ionize the hydrogen gas (thus clearing the fog). A recent study also suggested that black holes that existed in the early Universe created the necessary “winds” that allowed this ionizing radiation to escape.
To this end, FRBs could be used to probe into this early period of the Universe and determine what broke down this “fog” and allowed light to escape. Studying very distant FRBs could allow scientists to study where, when and how this process of “reionization” occurred. Looking ahead, Fialkov and Loeb explained how future radio telescopes will be able to discover many FRBs.
The planned Square Kilometer Array will be the world’s largest radio telescope when it begins operations in 2018. Credit: SKA
“Future radio observatories, like the Square Kilometer Array, will be sensitive enough to detect FRBs from the first generation of galaxies at the edge of the observable universe,” said Prof. Loeb. “Our work provides the first estimate of the number and properties of the first flashes of radio waves that lit up in the infant universe.”
And then there’s the Canadian Hydrogen Intensity Mapping Experiment (CHIME) at the at the Dominion Radio Astrophysical Observatory in British Columbia, which recently began operating. These and other instruments will serve as powerful tools for detecting FRBs, which in turn could be used to view previously unseen regions of time and space, and unlock some of the deepest cosmological mysteries.
“[W]e find that a next generation telescope (with a much better sensitivity than the existing ones) is expected to see many more FRBs than what is observed today,” said Dr. Fialkov. “This would allow to characterize the population of FRBs and identify their origin. Understanding the nature of FRBs will be a major breakthrough. Once the properties of these sources are known, FRBs can be used as cosmic beacons to explore the Universe. One application is to study the history of reionization (cosmic phase transition when the inter-galactic gas was ionized by stars).”
It is an inspired thought, using natural cosmic phenomena as research tools. In that respect, using FRBs to probe the most distant objects in space (and as far back in time as we can) is kind of like using quasars as navigational beacons. In the end, advancing our knowledge of the Universe allows us to explore more of it.
You might think you’re reading an educational website, where I explain fascinating concepts in space and astronomy, but that’s not really what’s going on here.
What’s actually happening is that you’re tagging along as I learn more and more about new and cool things happening in the Universe. I dig into them like a badger hiding a cow carcass, and we all get to enjoy the cache of knowledge I uncover.
Okay, that analogy got a little weird. Anyway, my point is. Squirrel!
Fast radio bursts are the new cosmic whatzits confusing and baffling astronomers, and now we get to take a front seat and watch them move through all stages of process of discovery.
Stage 1: A strange new anomaly is discovered that doesn’t fit any current model of the cosmos. For example, strange Boyajian’s Star. You know, that star that probably doesn’t have an alien megastructure orbiting around it, but astronomers can’t rule that out just yet?
Stage 2: Astronomers struggle to find other examples of this thing. They pitch ideas for new missions and scientific instruments. No idea is too crazy, until it’s proven to be too crazy. Examples include dark matter, dark energy, and that idea that we’re living in a
Stage 3: Astronomers develop a model for the thing, find evidence that matches their predictions, and vast majority of the astronomical community comes to a consensus on what this thing is. Like quasars and gamma ray bursts. YouTuber’s make their videos. Textbooks are updated. Balance is restored.
Today we’re going to talk about Fast Radio Bursts. They just moved from Stage 1 to Stage 2. Let’s dig in.
Fast radio bursts, or FRBs, or “Furbys” were first detected in 2007 by the astronomer Duncan Lorimer from West Virginia University.
He was looking through an archive of pulsar observations. Pulsars, of course, are newly formed neutron stars, the remnants left over from supernova explosions. They spin rapidly, blasting out twin beams of radiation. Some can spin hundreds of times a second, so precisely you could set your watch to them.
Lorimer’s archive of pulsar observations was captured at the Parkes radio dish in Australia. Credit: CSIRO (CC BY 3.0)
In this data, Lorimer made a “that’s funny” observation, when he noticed one blast of radio waves that squealed for 5 milliseconds and then it was gone. It didn’t match any other observation or prediction of what should be out there, so astronomers set out to find more of them.
Over the last 10 years, astronomers have found about 25 more examples of Fast Radio Bursts. Each one only lasts a few milliseconds, and then fades away forever. A one time event that can appear anywhere in the sky and only last for a couple milliseconds and never repeats is not an astronomer’s favorite target of study.
Actually, one FRB has been found to repeat, maybe.
The question, of course, is “what are they?”. And the answer, right now is, “astronomers have no idea.”
In fact, until very recently, astronomers weren’t ever certain they were coming from space at all. We’re surrounded by radio signals all the time, so a terrestrial source of fast radio bursts seems totally logical.
About a week ago, astronomers from Australia announced that FRBs are definitely coming from outside the Earth. They used the Molonglo Observatory Synthesis Telescope (or MOST) in Canberra to gather data on a large patch of sky.
Then they sifted through 1,000 terabytes of data and found just 3 fast radio bursts. Three.
Since MOST is farsighted and can’t perceive any radio signals closer than 10,000 km away, the signals had to be coming outside planet Earth. They were “extraterrestrial” in origin.
Right now, fast radio bursts are infuriating to astronomers. They don’t seem to match up with any other events we can see. They’re not the afterglow of a supernova, or tied in some way to gamma ray bursts.
In order to really figure out what’s going on, astronomers need new tools, and there’s a perfect instrument coming. Astronomers are building a new telescope called the Canadian Hydrogen Intensity Mapping Experiment (or CHIME), which is under construction near the town of Penticton in my own British Columbia.
CHIME under construction in Penticton, British Columbia. Credit: Mateus A. Fandiño (CC BY-SA 4.0)
It looks like a bunch of snowboard halfpipes, and its job will be to search for hydrogen emission from distant galaxies. It’ll help us understand how the Universe was expanding between 7 and 11 billion years ago, and create a 3-dimensional map of the early cosmos.
In addition to this, it’s going to be able to detect hundreds of fast radio bursts, maybe even a dozen a day, finally giving astronomers vast pools of signals to study.
What are they? Astronomers have no idea. Seriously, if you’ve got a good suggestion, they’d be glad to hear it.
In these kinds of situations, astronomers generally assume they’re caused by exploding stars in some way. Young stars or old stars, or maybe stars colliding. But so far, none of the theoretical models match the observations.
This artist’s conception illustrates one of the most primitive supermassive black holes known (central black dot) at the core of a young, star-rich galaxy. Image credit: NASA/JPL-Caltech
Another idea is black holes, of course. Specifically, supermassive black holes at the hearts of distant galaxies. From time to time, a random star, planet, or blob of gas falls into the black hole. This matter piles upon the black hole’s event horizon, heats up, screams for a moment, and disappears without a trace. Not a full on quasar that shines for thousands of years, but a quick snack.
The next idea comes with the only repeating fast radio burst that’s ever been found. Astronomers looked through the data archive of the Arecibo Observatory in Puerto Rico and found a signal that had repeated at least 10 times in a year, sometimes less than a minute apart.
Since the quick blast of radiation is repeating, this rules out a one-time collision between exotic objects like neutron stars. Instead, there could be a new class of magnetars (which are already a new class of neutron stars), that can release these occasional shrieks of radio.
An artist’s impression of a magnetar. Credit: ESO/L. Calçada
Or maybe this repeating object is totally different from the single events that have been discovered so far.
Here’s my favorite idea. And honestly, the one that’s the least realistic. What I’m about to say is almost certainly not what’s going on. And yet, it can’t be ruled out, and that’s good enough for my fertile imagination.
Avi Loeb and Manasvi Lingam at Harvard University said the following about FRBs:
“Fast radio bursts are exceedingly bright given their short duration and origin at distances, and we haven’t identified a possible natural source with any confidence. An artificial origin is worth contemplating and checking.”
Artificial origin. So. Aliens. Nice.
Loeb and Lingam calculated how difficult it would be to send a signal that strong, that far across the Universe. They found that you’d need to build a solar array with twice the surface area of Earth to power the radio wave transmitter.
And what would you do with a transmission of radio or microwaves that strong? You’d use it to power a spacecraft, of course. What we’re seeing here on Earth is just the momentary flash as a propulsion beam sweeps past the Solar System like a lighthouse.
But in reality, this huge solar array would be firing out a constant beam of radiation that would propel a massive starship to tremendous speeds. Like the Breakthrough Starshot spacecraft, but for million tonne spaceships.
Credit: NASA/Pat Rawlings (SAIC)
In other words, we could be witnessing alien transportation systems, pushing spacecraft with beams of energy to other worlds.
And I know that’s probably not what’s happening. It’s not aliens. It’s never aliens. But in my mind, that’s what I’m imagining.
So, kick back and enjoy the ride. Join us as we watch astronomers struggle to understand what fast radio bursts are. As they invalidate theories, and slowly unlock one of the most thrilling mysteries in modern astronomy. And as soon as they figure it out, I’ll let you know all about it.
What do you think? Which explanation for fast radio bursts seems the most logical to you? I’d love to hear your thoughts and wild speculation in the comments.
