force Archives

May 17, 2016May 17, 2016 by Matt Williams

What Is Air Resistance?

Space Travel — Atlantis Breaks Through the Clouds

Here on Earth, we tend to take air resistance (aka. “drag”) for granted. We just assume that when we throw a ball, launch an aircraft, deorbit a spacecraft, or fire a bullet from a gun, that the act of it traveling through our atmosphere will naturally slow it down. But what is the reason for this? Just how is air able to slow an object down, whether it is in free-fall or in flight?

Because of our reliance on air travel, our enthusiasm for space exploration, and our love of sports and making things airborne (including ourselves), understanding air resistance is key to understanding physics, and an integral part of many scientific disciplines. As part of the subdiscipline known as fluid dynamics, it applies to fields of aerodynamics, hydrodynamics, astrophysics, and nuclear physics (to name a few).

Definition:

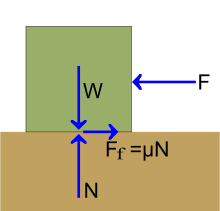
By definition, air resistance describes the forces that are in opposition to the relative motion of an object as it passes through the air. These drag forces act opposite to the oncoming flow velocity, thus slowing the object down. Unlike other resistance forces, drag depends directly on velocity, since it is the component of the net aerodynamic force acting opposite to the direction of the movement.

Another way to put it would be to say that air resistance is the result of collisions of the object’s leading surface with air molecules. It can therefore be said that the two most common factors that have a direct effect upon the amount of air resistance are the speed of the object and the cross-sectional area of the object. Ergo, both increased speeds and cross-sectional areas will result in an increased amount of air resistance.

This picture shows a bullet and the air flowing around it, giving visual representation to air resistance. Credits: Andrew Davidhazy/Rochester Institute of Technology — *Picture showing a bullet and the air flowing around it, giving visual representation to air resistance. Credits: Andrew Davidhazy/Rochester Institute of Technology*

In terms of aerodynamics and flight, drag refers to both the forces acting opposite of thrust, as well as the forces working perpendicular to it (i.e. lift). In astrodynamics, atmospheric drag is both a positive and a negative force depending on the situation. It is both a drain on fuel and efficiency during lift-off and a fuel savings when a spacecraft is returning to Earth from orbit.

Calculating Air Resistance:

Air resistance is usually calculated using the “drag equation”, which determines the force experienced by an object moving through a fluid or gas at relatively large velocity. This can be expressed mathematically as:

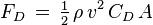
$F_D\, =\, \tfrac12\, \rho\, v^2\, C_D\, A$

In this equation, FD represents the drag force, p is the density of the fluid, v is the speed of the object relative to sound, A is the cross-section area, and CD is the the drag coefficient. The result is what is called “quadratic drag”. Once this is determined, calculating the amount of power needed to overcome the drag involves a similar process, which can be expressed mathematically as:

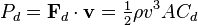
$P_d = \mathbf{F}_d \cdot \mathbf{v} = \tfrac12 \rho v^3 A C_d$

Here, Pd is the power needed to overcome the force of drag, Fd is the drag force, v is the velocity, p is the density of the fluid, v is the speed of the object relative to sound, A is the cross-section area, and Cd is the the drag coefficient. As it shows, power needs are the cube of the velocity, so if it takes 10 horsepower to go 80 kph, it will take 80 horsepower to go 160 kph. In short, a doubling of speed requires an application of eight times the amount of power.

*An F-22 Raptor reaching a velocity high enough to achieve a sonic boom. Credit: strangesounds.org*

Types of Air Resistance:

There are three main types of drag in aerodynamics – Lift Induced, Parasitic, and Wave. Each affects an objects ability to stay aloft as well as the power and fuel needed to keep it there. Lift induced (or just induced) drag occurs as the result of the creation of lift on a three-dimensional lifting body (wing or fuselage). It has two primary components: vortex drag and lift-induced viscous drag.

The vortices derive from the turbulent mixing of air of varying pressure on the upper and lower surfaces of the body. These are needed to create lift. As the lift increases, so does the lift-induced drag. For an aircraft this means that as the angle of attack and the lift coefficient increase to the point of stall, so does the lift-induced drag.

By contrast, parasitic drag is caused by moving a solid object through a fluid. This type of drag is made up of multiple components, which includes “form drag” and “skin friction drag”. In aviation, induced drag tends to be greater at lower speeds because a high angle of attack is required to maintain lift, so as speed increases this drag becomes much less, but parasitic drag increases because the fluid is flowing faster around protruding objects increasing friction. The combined overall drag curve is minimal at some airspeeds and will be at or close to its optimal efficiency.

*Space Shuttle Columbia launching on its maiden voyage on April 12th, 1981. Credit: NASA*

Wave drag (compressibility drag) is created by the presence of a body moving at high speed through a compressible fluid. In aerodynamics, wave drag consists of multiple components depending on the speed regime of the flight. In transonic flight – at speeds of Mach 0.5 or greater, but still less than Mach 1.0 (aka. speed of sound) – wave drag is the result of local supersonic flow.

Supersonic flow occurs on bodies traveling well below the speed of sound, as the local speed of air on a body increases when it accelerates over the body. In short, aircraft flying at transonic speeds often incur wave drag as a result. This increases as the speed of the aircraft nears the sound barrier of Mach 1.0, before becoming a supersonic object.

In supersonic flight, wave drag is the result of oblique shockwaves formed at the leading and trailing edges of the body. In highly supersonic flows bow waves will form instead. At supersonic speeds, wave drag is commonly separated into two components, supersonic lift-dependent wave drag and supersonic volume-dependent wave drag.

Understanding the role air frictions plays with flight, knowing its mechanics, and knowing the kinds of power needed to overcome it, are all crucial when it comes to aerospace and space exploration. Knowing all this will also be critical when it comes time to explore other planets in our Solar System, and in other star systems altogether!

We have written many articles about air resistance and flight here at Universe Today. Here’s an article on What Is Terminal Velocity?, How Do Planes Fly?, What is the Coefficient of Friction?, and What is the Force of Gravity?

If you’d like more information on NASA’s aircraft programs, check out the Beginner’s Guide to Aerodynamics, and here’s a link to the Drag Equation.

We’ve also recorded many related episodes of Astronomy Cast. Listen here, Episode 102: Gravity.

December 10, 2010May 16, 2016 by Matt Williams

What is the Coefficient of Friction?

Ever watch a car spin its wheels and notice all the smoke and tire marks it leaves behind? How about going down a slide? You might have noticed that if it were wet, you travelled farther than if the surface was dry. Ever wonder just how far you’d get if you tried to slide on wet concrete (don’t this, by the way!). Why is it that some surfaces are easy to slide across while others are just destined to stop you short? It comes down to a little thing known as friction, which is essentially the force that resists surfaces from sliding against each other. When it comes to measuring friction, the tool which scientists use is called the Coefficient of Friction or COH.

The COH is the value which describes the ratio of the force of friction between two bodies and the force pressing them together. They range from near zero to greater than one, depending on the types of materials used.For example, ice on steel has a low coefficient of friction, while rubber on pavement (i.e. car tires on the road) has a comparatively high one. In short, rougher surfaces tend to have higher effective values whereas smoother surfaces have lower due to the friction they generate when pressed together.

There are essentially two kind of coefficients; static and kinetic. The static coefficient of friction is the coefficient of friction that applies to objects that are motionless. The kinetic or sliding coefficient of friction is the coefficient of friction that applies to objects that are in motion.The coefficient of friction is not always the same for objects that are motionless and objects that are in motion; motionless objects often experience more friction than moving ones, requiring more force to put them in motion than to sustain them in motion.

Most dry materials in combination have friction coefficient values between 0.3 and 0.6. Values outside this range are rarer, but teflon, for example, can have a coefficient as low as 0.04. A value of zero would mean no friction at all, which is elusive at best, whereas a value above 1 would mean that the force required to slide an object along the surface is greater than the normal force of the surface on the object.

Mathematically, frictional force can be expressed asFf= ? N, where Ff = frictional force (N, lb), ? = static (?s) or kinetic (?k) frictional coefficient, N = normal force (N, lb).

We have written many articles about the coefficient of friction for Universe Today. Here’s an article about friction, and here’s an article about aerobraking.

If you’d like more info on the Friction, check out Hyperphysics, and here’s a link to Friction Games for Kids by Science Kids.

We’ve also recorded an entire episode of Astronomy Cast all about Gravity. Listen here, Episode 102: Gravity.

Sources:
http://en.wikipedia.org/wiki/Friction
http://www.engineeringtoolbox.com/friction-coefficients-d_778.html
http://www.thefreedictionary.com/coefficient+of+friction

September 14, 2010May 16, 2016 by Fraser Cain

What Is Terminal Velocity?

The higher you are when you jump, the more it hurts when you hit the ground. That’s because the Earth’s gravity is constantly accelerating you towards its center. But there’s actually a maximum speed you reach, where the acceleration of the Earth’s gravity is balanced by the air resistance of the atmosphere. The maximum speed is called terminal velocity.

The terminal velocity speed changes depending on the weight of the object falling, its surface area and what it’s falling through. For example, a feather doesn’t weigh much and presents a very large surface area to the air as it falls. So its terminal velocity speed is much slower than a rock with the same weight. This is why an ant can fall off a tall building and land unharmed, while a similar fall would kill you. Keep in mind that this process happens in any gas or fluid. So terminal velocity defines the speed that a rock sinks when you drop it in the water.

So, let’s say you’re a skydiver jumping out of an airplane. What’s the fastest speed you’ll go? The terminal velocity of a skydiver in a free-fall position, where they’re falling with their belly towards the Earth is about 195 km/h (122 mph). But they can increase their speed tremendously by orienting their head towards the Earth – diving towards the ground. In this position, the skydiver’s velocity increases to more than 400 km/h.

The world skydiving speed record is held by Joseph Kittinger, who was able to fall at a speed of 988 km/h by orienting his body properly and jumping at high altitude, where there’s less wind resistance.

The gravity of the Earth pulls at you with a constant acceleration of 9.81 meters/second. Without any wind resistance, you’ll fall 9.81 meters/second faster every second. 9.81 meters/second the first second, 19.62 meters/ second in the next second, etc.

The opposing force of the atmosphere is called drag. And the amount of drag force increases approximately proportional to the square of the speed. So if you double your speed, you experience a squaring of the drag force. Since the drag force is going up much more quickly than the constant acceleration, you eventually reach a perfect balance between the force of gravity and the drag force of whatever you’re moving through.

Outside the Earth’s atmosphere, though, there’s no terminal velocity. You’ll just keep on accelerating until you smash into whatever’s pulling on you.

We have written many articles about the terminal velocity for Universe Today. Here’s an article featuring the definition of velocity, and here’s an article about the X-Prize Entrant completing the Drop Test

If you’d like more info on the Terminal Velocity, check out a Lecture on Terminal Velocity, and here’s a link to a NASA article entitled, The Way Things Fall.

We’ve also recorded an entire episode of Astronomy Cast all about Gravity. Listen here, Episode 102: Gravity.

Sources:
NASA
Wikipedia
GSU Hyperphysics

July 19, 2009October 18, 2016 by John Carl Villanueva

What is the Gravitational Constant?

Visualization of a massive body generating gravitational waves (UWM)

The gravitational constant is the proportionality constant used in Newton’s Law of Universal Gravitation, and is commonly denoted by G. This is different from g, which denotes the acceleration due to gravity. In most texts, we see it expressed as:

G = 6.673×10^-11 N m² kg^-2

It is typically used in the equation:

F = (G x m₁ x m₂) / r² , wherein

F = force of gravity

G = gravitational constant

m₁ = mass of the first object (lets assume it’s of the massive one)

m₂ = mass of the second object (lets assume it’s of the smaller one)

r = the separation between the two masses

As with all constants in Physics, the gravitational constant is an empirical value. That is to say, it is proven through a series of experiments and subsequent observations.

Although the gravitational constant was first introduced by Isaac Newton as part of his popular publication in 1687, the Philosophiae Naturalis Principia Mathematica, it was not until 1798 that the constant was observed in an actual experiment. Don’t be surprised. It’s mostly like this in physics. The mathematical predictions normally precede the experimental proofs.

Anyway, the first person who successfully measured it was the English physicist, Henry Cavendish, who measured the very tiny force between two lead masses by using a very sensitive torsion balance. It should be noted that, after Cavendish, although there have been more accurate measurements, the improvements on the values (i.e., being able to obtain values closer to Newton’s G) have not been really substantial.

Looking at the value of G, we see that when we multiply it with the other quantities, it results in a rather small force. Let’s expand that value to give you a better idea on how small it really is: 0.00000000006673 N m² kg^-2

Alright, let’s now see what force would two 1-kg objects exert on one another when their geometrical centers are spaced 1 meter apart. So, how much do we get?

F = 0.00000000006673 N. It really doesn’t matter much if we increase both masses substantially.

For example, let’s try the heaviest recorded mass of an elephant, 12,000 kg. Assuming we have two of these, spaced 1 meter apart from their centers. I know it’s difficult to imagine that since elephants are rather stout, but let’s just proceed this way because I want to put emphasis on the significance of G.

So, how much did we get? Even if we rounded that off, we’d still obtain only 0.01 N. For comparison, the force exerted by the earth on an apple is roughly 1 N. No wonder we don’t feel any force of attraction when we sit beside someone… unless of course you’re a male and that person is Megan Fox (still, it’d be safe to assume that the attraction would only be one way).

Therefore, the force of gravity is only noticeable when we consider at least one mass to be very massive, e.g. a planet’s.

Allow me to end this discussion with one more mathematical exercise. Assuming you know both your mass and your weight, and you know the radius of the earth. Plug those into the equation above and solve for the other mass. Voila! Wonder of wonders, you’ve just obtained the mass of the Earth.

You can read more about the gravitational constant here in Universe Today. Want to learn more about a new study that finds fundamental force hasn’t changed over time? There’s also some insights you can find among the comments in this article: Record Breaking “Dark Matter Web” Structures Observed Spanning 270 Million Light Years Across

There’s more about it at NASA. Here are a couple of sources there:

Here are two episodes at Astronomy Cast that you might want to check out as well:

Sources: