[/caption]
A remarkable finding of the early 21st century, that kind of sits alongside the Nobel prize winning discovery of the universe’s accelerating expansion, is the finding that the universe is geometrically flat. This is a remarkable and unexpected feature of a universe that is expanding – let alone one that is expanding at an accelerated rate – and like the accelerating expansion, it is a key feature of our current standard model of the universe.
It may be that the flatness is just a consequence of the accelerating expansion – but to date this cannot be stated conclusively.
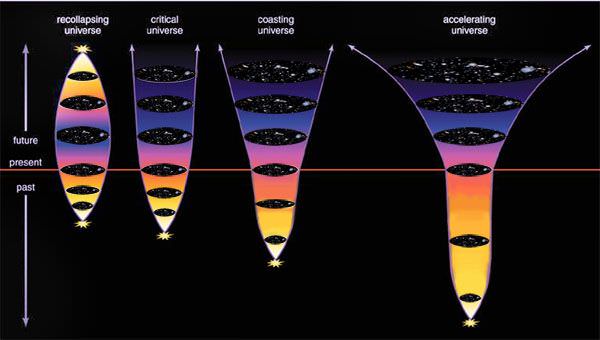
As usual, it’s all about Einstein. The Einstein field equations enable the geometry of the universe to be modelled – and a great variety of different solutions have been developed by different cosmology theorists. Some key solutions are the Friedmann equations, which calculate the shape and likely destiny of the universe, with three possible scenarios:
• closed universe – with a contents so dense that the universe’s space-time geometry is drawn in upon itself in a hyper-spherical shape. Ultimately such a universe would be expected to collapse in on itself in a big crunch.
• open universe – without sufficient density to draw in space-time, producing an outflung hyperbolic geometry – commonly called a saddle-shape – with a destiny to expand forever.
• flat universe – with a ‘just right’ density – although an unclear destiny.
The Friedmann equations were used in twentieth century cosmology to try and determine the ultimate fate of our universe, with few people thinking that the flat scenario would be a likely finding – since a universe might be expected to only stay flat for a short period, before shifting to an open (or closed) state because its expansion (or contraction) would alter the density of its contents.
Matter density was assumed to be key to geometry – and estimates of the matter density of our universe came to around 0.2 atoms per cubic metre, while the relevant part of the Friedmann equations calculated that the critical density required to keep our universe flat would be 5 atoms per cubic metre. Since we could only find 4% of the required critical density, this suggested that we probably lived in an open universe – but then we started coming up with ways to measure the universe’s geometry directly.
There’s a You-Tube of Lawrence Krauss (of Physics of Star Trek fame) explaining how this is done with cosmic microwave background data (from WMAP and earlier experiments) – where the CMB mapped on the sky represents one side of a triangle with you at its opposite apex looking out along its two other sides. The angles of the triangle can then be measured, which will add up to 180 degrees in a flat (Euclidean) universe, more than 180 in a closed universe and less than 180 in an open universe.
These findings, indicating that the universe was remarkably flat, came at the turn of the century around the same time that the 1998 accelerated expansion finding was announced.
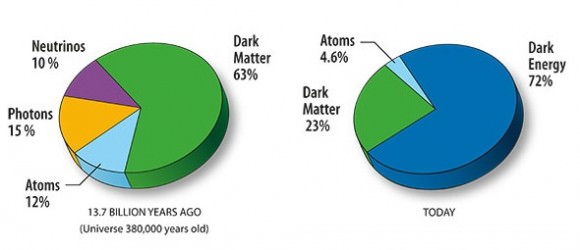
So really, it is the universe’s flatness and the estimate that there is only 4% (0.2 atoms per metre) of the matter density required to keep it flat that drives us to call on dark stuff to explain the universe. Indeed we can’t easily call on just matter, light or dark, to account for how our universe sustains its critical density in the face of expansion, let alone accelerated expansion – since whatever it is appears out of nowhere. So, we appeal to dark energy to make up the deficit – without having a clue what it is.
Given how little relevance conventional matter appears to have in our universe’s geometry, one might question the continuing relevance of the Friedmann equations in modern cosmology. There is more recent interest in the De Sitter universe, another Einstein field equation solution which models a universe with no matter content – its expansion and evolution being entirely the result of the cosmological constant.
De Sitter universes, at least on paper, can be made to expand with accelerating expansion and remain spatially flat – much like our universe. From this, it is tempting to suggest that universes naturally stay flat while they undergo accelerated expansion – because that’s what universes do, their contents having little direct influence on their long-term evolution or their large-scale geometry.
But who knows really – we are both literally and metaphorically working in the dark on this.
Further reading:
Krauss: Why the universe probably is flat (video).

The Universe appears flat because we are on the three-dimensional surface of a four-dimensional ripple expanding in space-time. It only appears to accelerate due to our perspective. Imagine a ripple in a pond. Drop a rock and a ripple expands from there at a constant speed. However, from the point of view of someone standing on the ripple, every other point on the ripple is accelerating away from him. So-called “Dark Energy” is just a trick of perspective.
I can’t see how the pond analogy delivers accelerating expansion – this is just an analogy for Hubble flow (i.e. coasting expansion) where things move faster the further away they are from you (due to cumulative coasting expansion).
What I don’t get is what’s powering this expansion. If its an infinite, and increasing expansion, where is the ever increasing energy needed for such a feat coming from.
I suspect the reality is that a collapse is coming at some point, we just don’t know what the trigger is. But like dark energy and matter overcoming the force of gravity, there could very well be some force that counteracts dark energy and matter at some point of the expansion. Don’t know…and we’re all just speculating anyway.
My belief is that the vacuum energy is powering the observed expansion of galaxies, and the universe space-time fabric is a dynamic metamaterial that is inseparable from the vacuum, magnetic fields, matter & anti-matter, etc.
Yes, general relativity makes space-time dynamic and inseparable from the matter-energy content within it.
Nitpick:
– We don’t observe galaxies expanding, we observe the universe expanding (in this case, large galaxy clusters are expanding).
Chernodub discovered magnetic fields in vacuum generate charged p mesons that behave like a superconductor along the magnetic field axis, and that behaves exactly like a metamaterial that can focus light in exotic ways, including a superlens, and also trap light like a black hole. They call the vacuum a hyperbolic metamaterial with detectable effects in the early light imaging of the universe. Seconds after the big-bang the early vacuum left huge imprints in the large-scale structures. I wonder if the great voids are not really better vacuums with less matter but more anti-matter? If this is true, would not gravity be a “3D metamaterial vacuum effect motion”, with no noticeable detectable effect using 2D gravity wave satellites? Since the vacuum is never empty, then there can be a magnetic field, which gives rise to everything
Since flat space means zero energy, there is no energy appearing or disappearing during expansion.
RickRyals commentary below goes into some of the technicalities behind such an innocuous claim.
In Einstein’s static cosmological model pressure equals zero when there is no matter. The cosmological constant came about because we do have matter and he needed something to reconcile this imbalance, but in order to get rho>0 out of Einstein’s matter-less static model, you have to condense the matter density from the existing structure, and in doing so the pressure of the vacuum necessarily becomes less than zero, P<0, thereby driving expansion via the "hole" that gets left in the vacuum when you rip a big chunk out of it to make a particle pair. The most obvious way to create new matter in Einstein's model, (which is also the most compatible with the spirit of general relativity), also holds it flat and stable, since the increase in negative pressure that the void creates is offset by the positive gravitation effect of the newly created massive particle even as expansion accelerates.
Too bad he didn't know about the real, massive particle potential of the quantum vacuum before he abandoned his most natural cosmological extension over a perceived instability problem that it really didn't have, huh?
The idea of the ‘real massive particle potential of the quantum vacuum’ is new to me – or do you just mean vacuum energy (which I am not sure you can get matter from).
Oh sure, it has long been thought that virtual particles can become real given enough energy. For example, according to quantum mechanics, virtual particle pairs in a region of strong gravitational tidal forces can be wrenched apart before they can annihilate, and when this happens in the region around a black hole, one particle may escape to survive indefinitely as its antiparticle partner is captured by the black hole.
Here’s another example:
http://www.newscientist.com/article/dn19327-lasers-could-make-virtual-particles-real.html
“These so-called “virtual particles” normally annihilate one another too quickly for us to notice them. But physicists predicted in the 1930s that a very strong electric field would transform virtual particles into real ones that we can observe. The field pushes them in opposite directions because they have opposite electric charges, separating them so that they cannot destroy one another.”
Gotcha – just vacuum energy leading to nett zero sum gain outside Planck units of time then. I’m not sure Einstein would have found this a satisfactory solution (i.e. something out of nothing) – though I can only guess of course.
But he wouldn’t look at it that way, as it falls naturally from his model that vacuum energy is very simply, rarefied ordinary mass energy that is less dense than ordinary matter until it gets condensed over a finite enough region of space to attain the matter density.
This also resolve the infamous “negative mass puzzle” as well. I think that he would have liked it.
Well, the appearance of virtual particle is a consequence of Heisenberg’s uncertainty principle. For a brief amount of time you can get a (huge) amount of energy “out of nowhere”, which can lead to the building of a particle pair, which normally annihilates again.
This effect is real, and can be observed with the Casimir-Effect.
It is also, as I understand, the basis for Hawking radiation.
Pie chart is wrong. Dark matter is placeholder for the unknown, could include an unknown property of atoms. Not exclusive concepts.
“You keep using that word. I do not think it means what you think it means.”
That word is never used in the context of theories. I challenge you to define it.
But I think you will find that either all components of a predictive theory are placeholders, because the theory can always be replaced or elaborated by later findings. Or that none are, because they are all predictive parts.
Cold dark matter is known to be that, because it behaves according to that prediction. And that is all we need in basic theory of standard cosmology.
The fact seems to be, you have found a “magical” word that you think excuse making contrafactual stuff up (“unknown”). Unfortunately, magic doesn’t work. =D
can anyone tell, why we cant see in our own past in the heavens ?
For the same reason that you can’t see yourself without the use of a mirror.
what is the universe imagined to be expanding into? solid neutrons?
it is most likely expanding into an even yet more tenuous ‘nothing’ that prevails in a greater state of ‘relaxation’ than the space proximal to matter and gravity. hence the accelerating expansion outward of ‘space’ with matter just going along for the ride.
horrifying!
Nitpick:
“You keep using that word. I do not think it means what you think it means.” =D
Besides the unfortunate juxtaposition of two different meanings, the latter claim is wrong. Space doesn’t expand “outward” since it isn’t expanding within a preexisting system. It is expanding, full stop.
I am sorry to pounce on this small nit, but a persistent wrong idea is supported by such unfortunate metaphor.
I have been trying to understand this for some time, in my fumbling layman way.
Before it was known that FRW universes are zero energy systems, the description used to be that inflation flattened space.
That could be extended to eternal inflation to predict that too curved universes would recollapse rapidly, making flatness seems a consequence of anthropic selection and/or perhaps a feature of multiverse statistics* (many attempts, but relatively small volumes at any given time).
I don’t know how well Faraoni et al zero energy prediction has fared in the theoretical physics community. Certainly it accords with what can be predicted by other means on general relativity despite its lack of a reasonable global energy definition. (Read lcrowell on this.)
And it is especially well suited to the simplest standard cosmology of exact flat space (and infinite universe), since now flatness can be interpreted as zero energy density.
However, it may be that flatness is an inherent characteristic of _consistent_ FRW cosmologies, whatever that means in practical terms besides “we have the standard cosmology and it works”. It certainly seems reasonable that a universe can expand from internal forces, as it must due to instability of GR cosmologies, without having energy somehow magically appear “from external sources”.
I think the above result shows that FRW universes are in cases reasonable and useful approximations to cosmologies.
de Sitter universes may have their uses as well, certainly they seem to be well liked by those who work on string and inflationary theory, but I don’t think they have spawned any testable predictions yet. Of course if you like anthropic selection they predict it, and in turn anthropic selection is the most predictive theory out there at the moment. So they are perhaps the next best thing.
[Added in posting: Wow, I certainly seem to use “certainly” a lot today! Maybe I need more coffee. Or more IVAN…]
————–
* If statistics over multiverses ever will make sense, that is. Still waiting on that one…
Thank you for a fresh note, Steve. Correcting one point may lead to a different perspective. You wrote “a universe might be expected to only stay flat for a short period, before shifting to an open (or closed) state because its expansion (or contraction) would alter the density of its contents.” Its not just this way. The geometry of space depends upon the density relative to the critical density and these two densities change in the same way during the expansion of the universe. So a universe that was initially closed will not change to an open universe later. It will remain closed.
The question why the geometry of our universe is as it is, is a question of initial conditions. There are infinitely many more curved universes that the single flat case. So if the geometry is the result of some sort of arbitrary quantum fluctuation, the probability that it is flat is zero. Hence we probably live in a curved universe, but the curvature is so small that we are not able to determine it.
The reason for this, and also for the expansion of the universe, may be found in what happened very early, in the first 10^(-33) second of the history of the universe – in the so-called inflationary era. In this incredibly brief period the universe was dominated by vacuum-energy with great density causing repulsive gravity. The universe exploded, and at the same time the density of the energy approached the critical density, characterizing a flat universe, exponentially fast. So the universe approached flatness exponentially fast, although it did not become quite flat. But the curvature diminished so much that we are not able to observere the difference from a flat universe.
Hence for all practical purposes, for example for calculating predictions, which is much simpler for a flat universe than for a curved one, we can consider our universe as flat.
Øyvind Grøn
Yes, that is an interpretation of inflation before the standard cosmology came around. (If we handwave at the problem that we can’t yet define probabilities over multiverses. And the other problem that supernova timing results indicates if not yet invalidates that geometry isn’t fluctuating at the Planck scale.)
In SC the probability that the geometry is flat can be”one” *, because it is the simplest parameter choice consistent with observations. But as I noted earlier, if universes are zero energy maybe this is a very natural constraint of whatever (then likely eternal) inflation mechanism we have.
————
* The unconstrained version is the usual parameter set given.
I think you are applying the modern interpretation. I was writing in the context of the traditional use of Friedmann equations where the contents of the universe does not change – so expansion leads to dilution (i.e. declining density).
Agree a closed universe can’t become an open one. A closed universe can expand for a while, but will begin to contract before it reaches critical density. Its future destiny can be determined at any point in its evolution. However, I can’t see how a flat universe could have been considered a stable solution under this traditional view.
I thought the flat case was analogous to an object leaving a body at exactly escape velocity with the positive and negative curvatures corresponding to lower or higher speeds, equivalent to elliptical, parabolic and hyperbolic Newtonian gravitational solutions.
Interesting theories, …
However, … it does bring to mind ancient times of the Roman Empire, …
Difference between ” The Universe & The Known Universe “.
After a couple of hard science deficient extrapolated rationales, …
This is basically a repeat of what I wrote on clearing out neutral hydrodgen at the end of the dark ages. Let the distance to some galaxy far away be x. I find that this distance x is changing, so I assign a scale factor a. So the time evolution of a distance x is given by
x = x(t) = a(t)x(0)
In this way this motion of any distant galaxy can be compared to this scale factor which expands (or contracts if that were to be the case) with the dynamics of the universe.
Now consider the next ingredient. The energy E of a particle of mass m moving in a central gravity field by some mass M at a distance r is
E = (1/2)mv^2 – GMm/r
The total energy E is constant, and largely can be ignored. In particular if the universe expands so there is no recollapse we can set it to zero. We concentrate on the velocity
v = dx/dt = x(0)(da/dt) = x(0)a’, prime means time derivative,
so that (1/2)mv^2 = (1/2)(a’)^2(x(0))^2. Now concentrate on the gravity part. We set r = x, the distance to other galaxies, and we assign an average density so that the mass M is a sum of all these galactic masses M = ?Vol. The volume out to some radial distance x is then Vol = (4?/3)x^3 = (4?/3)a^3(x(0))^3. We put all of this together and we get the equation
(a’/a)^2 = 8?G?/3.
This equation is close to what one gets with general relativity, where here we have just used Newtonian mechanics and gravity. There is with general relativity an additional –k/a^2 factor related to the constant energy E, which for a spatially flat universe has k = 0.
How the Hubble constant is H = (a’/a), which is a constant in space, but not necessarily in time. The Einstein cosmological constant is ? = 8?G? for some constant vacuum energy density ?, and so the Hubble parameter is then
H^2 = (a’/a)^2 = ?/3
For some other mass-energy density, such as matter or radiation, the density is dependent on the scale factor a.
For those familiar with differential equations the solution to a’ = sqrt{?/3}a is an exponential function. This is the expansion driven universe we do observe. For a small scale factor this exponential is approximately linear which gives the Hubble relation found in the 1920s v = Hd. So for a galaxy as a distance d the Hubble parameter multiplied by that distance gives the velocity. The Hubble parameter is approximately H = 72km/sec/Mpc. For the distance to some galaxy d in mega parsecs (Mpc) one gets the outwards velocity of that galaxy.
This Newtonian approach is modified so that
(a’/a)^2 = 8?G?/3 – k/a^2
in general relativity. For k = 1 this is a closed spherical cosmology, where the space is a 3-sphere that expands. The case k = 0 is the open flat space, which is the most likely case based on the data, which expands and foliates out spacetime with a curvature in the time direction. The k = -1 is the hyperbolic or saddle space. It is also worth noticing that since this additional term is k/a^2 then for the expansion factor very large this term is essentially zero. During inflation there was a 63 e-fold expansion or an increase in a by 10^{27}. So even if k = 1 this factor was 10^{-27} after inflation and has with subsequent cosmic expansion been dropped by 10^{-25} so that k/a^2 ~ 10^{-52}
LC