[/caption]
The so-called End of Greatness is where you give up trying to find more superlatives to describe large scale objects in the universe. Currently the Sloan Great Wall – a roughly organised collection of galactic superclusters partitioning one great void from another great void – is about where most cosmologists draw the line.
Beyond the End of Greatness, it’s best just to consider the universe as a holistic entity – and at this scale we consider it isotropic and homogenous, which we need to do to make our current cosmology math work. But at the very edge of greatness, we find the cosmic web.
The cosmic web is not a thing we can directly observe since its 3d structure is derived from red shift data to indicate the relative distance of galaxies, as well as their apparent position in the sky. When you pull all this together, the resulting 3d structure seems like a complex web of galactic cluster filaments interconnecting at supercluster nodes and interspersed by huge voids. These voids are bubble-like – so that we talk about structures like the Sloan Great Wall, as being the outer surface of such a bubble. And we also talk about the whole cosmic web being ‘foamy’.
It is speculated that the great voids or bubbles, around which the cosmic web seems to be organised, formed out of tiny dips in the primordial energy density (which can be seen in the cosmic microwave background), although a convincing correlation remains to be demonstrated.

As is well recorded, the Andromeda Galaxy is probably on a collision course with the Milky Way and they may collide in about 4.5 billion years. So, not every galaxy in the universe is rushing away from every other galaxy in the universe – it’s just a general tendency. Each galaxy has its own proper motion in space-time, which it is likely to continue to follow despite the underlying expansion of the universe.
It may be that much of the growing separation between galaxies is a result of expansion of the void bubbles, rather than equal expansion everywhere. It’s as though once gravity loses its grip between distant structures – expansion (or dark energy, if you like) takes over and that gap begins to expand unchecked – while elsewhere, clusters and superclusters of galaxies still manage to hold together. This scenario remains consistent with Edwin Hubble’s finding that the large majority of galaxies are rushing away from us, even if they are not all equally rushing away from each other.
van de Weygaert et al are investigating the cosmic web from the perspective of topology – a branch of geometry which looks at spatial properties which are preserved in objects undergoing deformation. This approach seems ideal to model the evolving large scale structure of an expanding universe.
The paper below represents an early step in this work, but shows that a cosmic web structure can be loosely modelled by assuming that all data points (i.e. galaxies) move outwards from the central point of the void they lie most proximal to. This rule creates alpha shapes, which are generalised surfaces that can be built over data points – and the outcome is a mathematically modelled foamy-looking cosmic web.
Further reading: van de Weygaert et al. Alpha Shape Topology of the Cosmic Web.

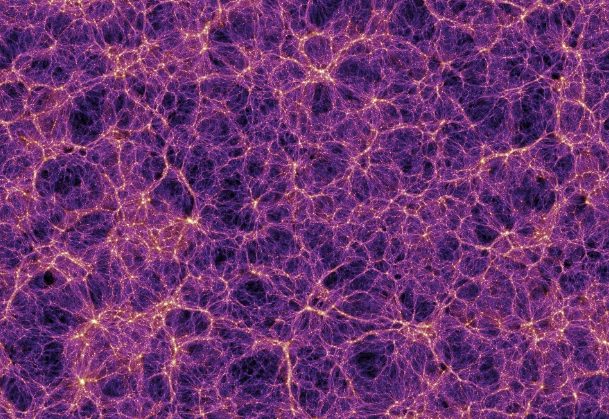
Gee, that picture looks almost like it’s some sort of large-scale P… nah, I better not say it; Crumb could be reading. Let’s just say that the picture sparks the imaginiation…
the sloan great wall is considered as being a part of the outer surface of a foamy bubble. Assuming innumerable superclusters have formed beyond our visible horizon, and inflation prevents a super dupper cluster or anything larger from forming in the universe, could the Penrose CMB rings be evidence for multi-verses?
Interesting find on alpha shapes, where topology meets geometry.
In the time honored tradition of science blogs, I’m going to nitpick/bitch about details instead of bothering with the Great Picture, at least for now.
First, and this is a mere category problem, but generally I would think mathematicians don’t see topology as a branch of geometry. YMMV, IANAM.
Geometry is, as the name alludes, interested in dimensional measures (lengths, areas, volumes) of space. Topology, once inspired by geometry, is interested in what “remains” of structure in spaces when dimensions are not considered (other than obliquely). Geometry is a specific branch of mathematics, topology is a great unifier of mathematics.
Second, and this is mere poetic license I feel, is the characterizations of the End of Greatness and the universe.
The former is the scale where the universe goes towards the predicted uniformity – but the link tells us that. It is a Greatness [sic!] example of humor.
The later OTOH is a pet peeve of mine, since “holism” is originally a postmodern anti-scientific idea as I have understood it. So I don’t like to see its use, or rather my hackles rises and my bile with it. 😀 As the postmodern idea of subjectivity of science, holism has been soundly rejected on account of the dearth of examples.
The text itself contains a specific rejection of the universe as holistic, since emergence rejects holism and here we have the emergence of structure. … prrftthh on holism!
[Hmm. As I’m writing this I get the feeling we have been here before, on holism. But it takes forever to google up similar threads, and whatever I said then I’m likely to say now on this subject since it is precisely not a fruitful topic within science. Oh, well.
And yay, my spell checker is “holism” naive! FF FTW!]
Agree topology is more correctly math. Holistic is a useful word that pre-dates hippy psuedoscience. We should steal it back 🙂
can dark energy be responsible for expanding and forming these great cosmic void bubbles, where cosmological objects beyond known size could exist dubbed as super duper clusters? Dark energy and gravity are inversely proportional forces by distance. it seems most Likely that both gravity and EM forces shape the universe.
As for shaping, it is definitely a response to gravity (with the help of dark energy as the article says). The reason is that gravity has one charge, mass, while the EM field has two opposite polarized ones.
Hence gravity, despite being the weakest force (maybe counting DE out, I haven’t checked), sums up to cosmological structures. EM charges OTOH cancels out.
Since the topic is so often raised in these pages, despite this being early school material for sure, if I was a “EM universe” pseudoscience religious believer, I would try to redirect my fantasies to DE. Perhaps it is the residual zero energy of the vacuum fields as in the most natural hypothesis, of which EM would be a part. In that sense their fantasies would be a little more relevant and a little less harmful for understanding nature.
Oh, I forgot this:
I think that inflation puts a limit on structure.
Modulo the “convincing correlation” of the article, I think it is believed that since the observed structure matches expected primordial vacuum energy fluctuations on scale (I think), it would then be no larger structure to be found.
That is, in the local region of end of inflation. The next level up is then the structure of the multiverse, with vacuum energy bubbles stochastically relaxing towards lower energies and, possibly, chaotic structure of inflated regions in some volumes of inflation models parameter space.
Its the bubbles of nothing that make it something. 🙂
Leading to suggest that the nothing is in fact something
And there is a whole lot more of the nothing pushing against the visible something. However the visible something seems to be all connected throughout the nothing. And past a certain unobservable point it may as well be nothing as we will never see it.
Er, so is it the nothing pushing the something apart or is the visible something growing out of the nothing. ?
Besides who needs superlatives when we can just anthropomorphize it into something our puny rational minds can deal with.
“The foamy-looking cosmic web computer model image looks like images of brain synapses to me.” There; we live in a gargantuan cosmic brain. 🙂
Nitpick: “Hubble has sometimes been incorrectly credited with discovering the Doppler shift in the spectra of galaxies, but this had already been observed earlier by Vesto Slipher, whose data Hubble used.”
Credit where credit is due, although Hubble deduced from the data that the Universe was expanding. Pity we still don’t definitively know why…
The authors employ homology theory. A brief idea of that is maybe in order. I thought I would give some indication of what that is before getting to the cosmology. This requires some qualitative description of mathematics, and mathematical thinking is healthy if you want to understand physical science.
The core of the idea behind homology can be seen in the difference between a 2 dimensional sphere and a 2-d torus. With the sphere any loop on the surface can be extended into any other loop of any size, and indeed contracted to a point. Therefore the topological information it contains is zero. The sphere may also be chopped in two with a region of overlap, eg a thickened equator. These two disks when sutured together recover the sphere. However, one can’t be continuously extended into the other. The reason is similar to the fact that a map of the Earth with the North Pole at the center is not able to cover the South Pole. There is a stereographic projection of the South Pole to infinity. So the stereographic projection has an infinite number of extensions, which is the real numbers. A discrete version of this is a set of integers. Similarly, the North and South Poles when removed give a sheet that can’t cover the N and S poles (the blow up of the Mercator map) and so points have a projective map. So there are the homology groups (or rings) for zero dimensional objects in the space which is R or Z (reals or integers), the one dimensional elements have no topological information so that is 0, and the two dimensional stuff has again R or Z. The distinction between R and Z is a technical matter, which I will avoid here. So we have these elements call homology rings that are
H_0(S) = Z
H_1(S) = 0
H_2(S) = Z.
For a higher dimensional sphere (dim = n) you have H_0(S) = Z and H_n(S) = Z and all others zero.
Now consider the torus. We can make a torus from the sphere by removing the antipodal points (N and S poles) and by identifying the infinitesimal boundaries left behind. This removed the H_0 and H_2 topology and replaces them with something else. If I remove a point from the torus and expand the hole into a disk and push further until there is no area left I am left with two curves connected at a point. So this means H_0(T) = Z. For H_1 we have that on that inner tube and there are two closed curves which can’t be deformed into each other. One curve encloses the tube and the other might be seen as the seem line on the inner tube. You might have to think a bit, but you can convince yourselves of this. So we have H_1(T) = Z+Z and H_2(T) being dual to H_0(T) is also Z. In fact for the n-dimensional torus you have H_p(T) = 0 for p > 2 and the same as case above for p = 0, 1, and 2. .
I used a bit of something called homotopy theory (another approach to topology) to illustrate the curves. These homology rings have a basic algebraic property. The first of these is that the boundary of a boundary is zero. A 2-sphere is the boundary of a 3-ball, but the 2-sphere itself has no boundary. So for d the boundary operator this rule is that d*d = d^2 = 0. Now think of the torus. Those two curves that can’t be extended into each other enclose nothing on the torus. So those curves are not the boundary of any space pertinent to the torus. Think of cutting the torus along the curve enclosing the tube. This then constructs a cylinder, but since the boundary of this is really the same curve I can contract this cylinder into a ring. So there is no actual content to these curves being the boundary of anything in the torus. Yet the boundary operator on these curves is zero. Why? Further, these closed curves themselves have no boundary. The boundary operator d on the curves C is zero and H_1(T) as the homology over these curves, then dC = 0 (the curves have no boundary) and further C =/= dB, for B some 2 dimensional object the curves bound. The homology ring is then
H_1(T) = ker(d)/im(d)
It is the kernel of the boundary operator (dC = 0) but modulo (not including) any elements formed from d (as in dB for some B) which is the image of d (im(d)). This definition is a way of reducing topology to elements of abstract algebra. For this reason the subject is called algebraic topology.
The matter of Betti numbers can then be seen in the rank of these homology groups. The Betti numbers are then b_p = rank(H_p(M)) for M the manifold. So for the sphere you have the Betti numbers b_0 = 1, b_1 = 0 and b_2 = 1. For the Torus we have b_0 = 1, b_1 = 2 and b_2 = 1. These may then be used to compute the Euler characteristic
X = 2 sum_p(-1)^pb_p,
which for the Sphere is 2(1 – 0 + 1) = 2 and for the torus is 2(1 – 2 + 1) = 0.
So this is a rule of thumb sort of whirlwind tour of algebraic topology. If you want to read the paper by van de Weygaert some of this might clarify some of the mathematics in the paper. The authors construct these alpha shapes for the bubbles by a combinatorics on vertices, edgelinks, and cells. IN fact on paper 2 this is referenced as combinatorial topology. So the construction of these voids according to a discrete topology, and maybe with alpha shapes within alpha shapes, is a way of describing this webbing of threads, walls and voids.
It would be interesting to work this into some sort of fractal topology, with alphas shapes in alpha shapes and so forth. A related issue is whether the Hausdorff dimension of this fractal has any relationship to the fractal geometry of the CMB anisotropy.
LC
Ah, I remember now – this was a very interesting characterization of cosmic structure that I saw somewhere (here?) a few months back. Good that they have continued!
I haven’t worked with algebraic topology (more than it has touched differential geometry, of which I have a passing acquaintance). But if Betti numbers is the rank that corresponds to unconnected surfaces, the paper notes that the number of voids (B_2) is limited in an alpha shape of cosmic structure (see fig 6).
The reason would be the obvious one, in reality there is no fractal but a size cut off. The CMB would have cut offs too of course.
[Btw, I note from the article link of alpha shapes that the dual problem would be space-filling (with balls, here). The shared rands would have the same cover, so the same Hausdorff dimension unless I’m mistaken.]
I believe I see where one would go with comparing fractals, which should still be possible with enough statistics and modeling. There is snag in the paper though AFAIU, where they note that their models indicate an (expected) shift in topology as the structures evolves from CMB quantum variations to aggregated matter:
“The steadily increasing contrast of the various structural features is accompanied by a gradual shift in topological nature of the distribution. The virtually uniform and featureless particle distribution at the beginning ultimately unfolds into a highly clumped distribution of almost only clusters (vertices). This evolution involves a gradual progression via a wall-like through a filamentary towards an ultimate clusterdominated matter distribution. By then nearly all matter has streamed into the nodal sites of the cellular network.”
Instead the paper discuss characterizing the number of (Betti) components and their evolution over time, a Betti frequency analysis if you will, to get to the underlying topologies.
I read the article, which true to most articles involving numerics is descriptive. So it is a bit tough for me to understand the details. This is soap bubble topology. The procedure appears to fill in smaller voids to increase the measure “alpha.”. The Voronoi tessellation process is a type of lattice building or sphere packing. This structure is similar to either a quasi-crystal or an amorphous solid.
I still ponder whether there is a fractal geometry to the filaments, webs and voids of the universe. The soap bubble analogy suggests there is some scaling parameter for the volume of different voids. Of course there is a cut off, for most physical systems that have fractal geometry have some cut-off in scale. This structure emerged from the CMB, and it is interesting to ponder whether the two fractal geometries have the same Hausdorff dimensions.
LC
http://www.youtube.com/watch?v=tZ8TJ4E_ihY
Notice the structures that appear around the 20 second mark.
Wow, Gnat that really looks like bing bang simulation 🙂
Singularity ‘flying’ through nothingness ‘hit’ something and here we go and have our dark energy (inflation) as a result of previous momentum.
I sort of got pilloried by Carroll and others on their Cosmic Variance for suggesting a fluid model for dark matter. I could of course be wrong, but in this business some caution combined with temerity is required.
LC