[/caption]
This time it was the gravitational redshift part of General Relativity; and the stringency? An astonishing better-than-one-part-in-100-million!
How did Steven Chu (US Secretary of Energy, though this work was done while he was at the University of California Berkeley), Holger Müler (Berkeley), and Achim Peters (Humboldt University in Berlin) beat the previous best gravitational redshift test (in 1976, using two atomic clocks – one on the surface of the Earth and the other sent up to an altitude of 10,000 km in a rocket) by a staggering 10,000 times?
By exploited wave-particle duality and superposition within an atom interferometer!
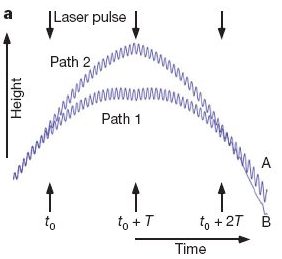
About this figure: Schematic of how the atom interferometer operates. The trajectories of the two atoms are plotted as functions of time. The atoms are accelerating due to gravity and the oscillatory lines depict the phase accumulation of the matter waves. Arrows indicate the times of the three laser pulses. (Courtesy: Nature).
Gravitational redshift is an inevitable consequence of the equivalence principle that underlies general relativity. The equivalence principle states that the local effects of gravity are the same as those of being in an accelerated frame of reference. So the downward force felt by someone in a lift could be equally due to an upward acceleration of the lift or to gravity. Pulses of light sent upwards from a clock on the lift floor will be redshifted when the lift is accelerating upwards, meaning that this clock will appear to tick more slowly when its flashes are compared at the ceiling of the lift to another clock. Because there is no way to tell gravity and acceleration apart, the same will hold true in a gravitational field; in other words the greater the gravitational pull experienced by a clock, or the closer it is to a massive body, the more slowly it will tick.
Confirmation of this effect supports the idea that gravity is geometry – a manifestation of spacetime curvature – because the flow of time is no longer constant throughout the universe but varies according to the distribution of massive bodies. Exploring the idea of spacetime curvature is important when distinguishing between different theories of quantum gravity because there are some versions of string theory in which matter can respond to something other than the geometry of spacetime.
Gravitational redshift, however, as a manifestation of local position invariance (the idea that the outcome of any non-gravitational experiment is independent of where and when in the universe it is carried out) is the least well confirmed of the three types of experiment that support the equivalence principle. The other two – the universality of freefall and local Lorentz invariance – have been verified with precisions of 10-13 or better, whereas gravitational redshift had previously been confirmed only to a precision of 7×10-5.
In 1997 Peters used laser trapping techniques developed by Chu to capture cesium atoms and cool them to a few millionths of a degree K (in order to reduce their velocity as much as possible), and then used a vertical laser beam to impart an upward kick to the atoms in order to measure gravitational freefall.
Now, Chu and Müller have re-interpreted the results of that experiment to give a measurement of the gravitational redshift.
In the experiment each of the atoms was exposed to three laser pulses. The first pulse placed the atom into a superposition of two equally probable states – either leaving it alone to decelerate and then fall back down to Earth under gravity’s pull, or giving it an extra kick so that it reached a greater height before descending. A second pulse was then applied at just the right moment so as to push the atom in the second state back faster toward Earth, causing the two superposition states to meet on the way down. At this point the third pulse measured the interference between these two states brought about by the atom’s existence as a wave, the idea being that any difference in gravitational redshift as experienced by the two states existing at difference heights above the Earth’s surface would be manifest as a change in the relative phase of the two states.
The virtue of this approach is the extremely high frequency of a cesium atom’s de Broglie wave – some 3×1025Hz. Although during the 0.3 s of freefall the matter waves on the higher trajectory experienced an elapsed time of just 2×10-20s more than the waves on the lower trajectory did, the enormous frequency of their oscillation, combined with the ability to measure amplitude differences of just one part in 1000, meant that the researchers were able to confirm gravitational redshift to a precision of 7×10-9.
As Müller puts it, “If the time of freefall was extended to the age of the universe – 14 billion years – the time difference between the upper and lower routes would be a mere one thousandth of a second, and the accuracy of the measurement would be 60 ps, the time it takes for light to travel about a centimetre.”
Müller hopes to further improve the precision of the redshift measurements by increasing the distance between the two superposition states of the cesium atoms. The distance achieved in the current research was a mere 0.1 mm, but, he says, by increasing this to 1 m it should be possible to detect gravitational waves, predicted by general relativity but not yet directly observed.
Sources: Physics World; the paper is in the 18 February, 2010 issue of Nature

It’s a far cry from Eddington’s expedition in 1919 to test GR by the deflection of light from distant stars by the Sun and the GR explanation of the anomalous rate of precession of the perihelion of Mercury’s orbit.
Well done Albert!
Wish all ‘theories’ could be tested like this!
This is an elegant result, or test.
LC
One of the best articles on UT lately: thanks!
Yes, elegant, but also useful. Who wouldn’t wish to observe gravitational waves anytime soon.
This is another win for GR. I believe someone recently noted that DM results test it across the universe to heretofore unrealized precision as well.
Yes, but still, it has nothing on biology.
Of course the complexity of the theory means orders of magnitude more tests. But the amazing fact to me is that the combinatorial nature of the contingencies of phylogenetic trees means that comparing the resulting handful of possible trees that come out of an analysis with observation amounts to testing evolutionary prediction to a precision of 10^-38!
“Nevertheless, a precision of just under 1% is still pretty good; it is not enough, at this point, to cause us to cast much doubt upon the validity and usefulness of modern theories of gravity. However, if tests of the theory of common descent performed that poorly, different phylogenetic trees, as shown in Figure 1, would have to differ by 18 of the 30 branches!
In their quest for scientific perfection, some biologists are rightly rankled at the obvious discrepancies between some phylogenetic trees (Gura 2000; Patterson et al. 1993; Maley and Marshall 1998). However, as illustrated in Figure 1, the standard phylogenetic tree is known to 38 decimal places, which is a much greater precision than that of even the most well-determined physical constants.
For comparison, the charge of the electron is known to only seven decimal places, the Planck constant is known to only eight decimal places, the mass of the neutron, proton, and electron are all known to only nine decimal places, and the universal gravitational constant has been determined to only three decimal places.”
There are a lot of caveats, of course.
– Certainly the reference plays loose and high with the definitions of “precision” and “uncertainty” both, as it applies to testing especially.
– Speaking of which, additions or removals of traits and/or species may change the tree geometry (sometimes even topology) much.
– There is also a known trade off between resolution and depth of time of these trees due to “long branch attraction”, i.e. reversals and complete loss of traits over deep time tends to move distant branches together in a model free analysis.
And those are only the objections this non-biologist can pull from the top of his head. I’m sure a biologist can add lots of them.
Still, it is a worthwhile comparison I think. It points out that both complexity and system contingency (which are mostly absent from physics outside of anthropic theories) may push the testing game to a whole different level of amount respectively precision.
Just wait and see what happens when physics catches up with biology!
I am looking at this in detail. I wrote a paper which won an honorable recognition by the Gravity Research Foundation in 2007 on a proposed experiment to detect the Unruh effect. It involved a rapid acceleration of a BEC through a capacitor. I wonder if this could be used to work with such physics. Detecting this sort of physics could be a way of experimentally looking at how black hole physics is related to elementary particles.
This experiment could be seen as a general Bohr wave experiment for a massive particle. The trajectory is a sum over histories, to use Wheeler’s term for a path integral, which constructively interferes with itself. This is a sort of “matter beam splitter” experiment, where any deviation from the equivalence principle would be analogous to an optical element on an optics bench.
LC