[/caption]
Mass: 1.98892 x 1030 kg
Diameter: 1,391,000 kilometers
Radius: 695,500 km
Surface gravity of the Sun: 27.94 g
Volume of the Sun: 1.412 x 1018 km3
Density of the Sun: 1.622 x 105 kg/m3
How Big is the Sun?
The Sun is the largest object in the Solar System, accounting for 99.86% of the mass.
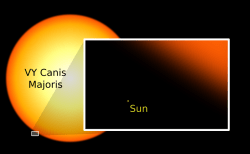
As stars go, the Sun is actually a medium-sized, and even smallish star. Stars with much more mass can be much larger than the Sun. For example, the red giant Betelgeuse, in the constellation of Orion is thought to be 1,000 times larger than the Sun. And the largest known star is VY Canis Majoris, measuring approximately 2,000 times larger than the Sun. If you could put VY Canis Majoris into our Solar System, it would stretch out past the orbit of Saturn.
The size of the Sun is changing. In the future when it runs out of usable hydrogen fuel in the core, it will become a red giant as well. It will engulf the orbits of Mercury and Venus, and possibly even the orbit of the Earth. For a few million years, the Sun will be about 200 times bigger than its current size.
After the Sun becomes a red giant, it will shrink down to become a white dwarf star. Then the size of the Sun will only be roughly the size of the Earth.
Mass of the Sun
The mass of the Sun is 1.98892 x 1030 kilograms. That’s a really big number, and it’s really hard to put it into context, so let’s write out the mass of the Sun, with all the zeros.
1,988,920,000,000,000,000,000,000,000,000 kilograms.
Still need to wrap your head around this? Let’s give you some comparisons. The mass of the Sun is 333,000 times the mass of the Earth. It’s 1,048 times the mass of Jupiter, and 3,498 times the mass of Saturn.
In fact, the Sun accounts for 99.8% of all the mass in the entire Solar System; and most of that non-Sun mass is Jupiter and Saturn. To say that the Earth is an insignificant speck is an understatement.
When astronomers try to gauge the mass of another star-like object, they use the mass of the Sun for comparison. This is known as a “solar mass”. So the mass of objects, like black holes, will be measured in solar masses. A massive star might have 5-10 solar masses. A supermassive black hole could have hundreds of millions of solar masses.
Astronomers will refer to this with an M beside a symbol that looks like a circle with a dot in the middle – M⊙. To show a star that has 5 times the mass of the Sun, or 5 solar masses, it would be 5 M⊙.
The Sun is massive, but it’s not the most massive star out there. In fact, the most massive star we know of is Eta Carinae, which has a mass of 150 times the mass of the Sun.
The Sun’s mass is actually slowly decreasing over time. There are two processes at work here. The first is the fusion reactions in the core of the Sun, converting atoms of hydrogen into helium. Some of the Sun’s mass is lost through the fusion process, as atoms of hydrogen are converted into energy. The warmth we feel from the Sun, is the Sun’s lost mass. The second way is the solar wind, which is constantly blowing protons and electrons into outer space.
Mass of the Sun in kilograms: 1.98892 x 1030 kg
Mass of the Sun in pounds: 4.38481 x 1030 pounds
Mass of the Sun in tons: 2.1924 x 1027 tons
Diameter of the Sun
The diameter of the Sun is 1.391 million kilometers or 870,000 miles.
Again, let’s put this number into perspective. The diameter of the Sun is 109 times the diameter of the Earth. It’s 9.7 times the diameter of Jupiter. Really, really big.
Pardon the pun, but the Sun doesn’t hold a candle to some of the largest stars in the Universe. The biggest star we know of is called VY Canis Majoris, and astronomers think it could be 2,100 times the diameter of the Sun.

Diameter of the Sun in kilometers: 1,391,000 km
Diameter of the Sun in miles: 864,000 miles
Diameter of the Sun in meters: 1,391,000,000 meters
Diameter of the Sun compared to Earth: 109 Earths
Radius of the Sun
The radius of the Sun, the measurement from the exact center of the Sun out to its surface, is 695,500 kilometers.
This radius is essentially the same however you measure it, from the center to the equator, or the from the center to the Sun’s poles. But you need to be careful with other objects, however, because the speed of their rotation affects the radius.
The Sun takes about 25 days to turn once on its axis. Because it rotates relatively slowly, the Sun doesn’t flatten out at all. The distance from the center to the poles is almost exactly the same as the distance from the center to the equator.
There are stars out there which are dramatically different, though. For example, the star Achernar, located in the constellation Eridanus, is flattened by 50%. In other words, the distance from the poles is half the distance across the equator. In this situation, the star actually looks like spinning-top toy.
So, relative to out stars out there, the Sun is almost a perfect sphere.
Astronomers use the Sun’s radius, or “solar radius” to compare the sizes of stars and other celestial bodies. For example, a star with 2 solar radii is twice as large as the Sun. A star with 10 solar radii is 10x as large as the Sun, and so on.
Polaris, the North Star, is the brightest star in the constellation Ursa Minor (Little Dipper) and, because of its proximity to the north celestial pole, is considered the current northern pole star. Polaris is primarily used for navigation and has a solar radius of 30. That means, it is 30 times bigger than the Sun.
Sirius which is the brightest star in the night sky. In terms of apparent magnitude, the second brightest star, Canopus, has only half that of Sirius’. No wonder it really stands out. Sirius is actually a binary star system, with Sirius A having a solar radius of 1.711 and B, which is much smaller, at about 0.0084.
Radius of the Sun in kilometers: 695,500 km
Radius of the Sun in miles: 432,200 miles
Radius of the Sun in meters: 695,500,000 meters
Radius of the Sun compared to Earth: 109 Earths
Gravity of the Sun
The Sun has an enormous amount of mass, and so it has a lot of gravity. In fact, the mass of the Sun is 333,000 times more than the mass of the Earth. Forget that the surface temperature of the Sun is 5,800 Kelvin and made of hydrogen – what would you feel if you could walk on the surface of the Sun? Think about this, the gravity of the Sun at the surface is 28 times the gravity of the Earth.
In other words, if your scale says 100 kg on Earth, it would measure 2,800 kg if you tried to walk on the surface of the Sun. Needless to say, you would die pretty quickly just from the pull of gravity, not to mention the heat, etc.
The Sun’s gravity pulls all of its mass (mostly hydrogen and helium) into an almost perfect sphere. Down at the core of the Sun, the temperatures and pressures are so high that fusion reactions are possible. The tremendous amount of light and energy pouring out of the Sun counteracts the pull of gravity trying to collapse it down.
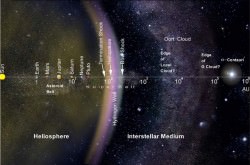
Astronomers define the Solar System as the distance under the influence of gravity from the Sun. We know that the Sun holds distant Pluto in orbit (5.9 billion km away on average). But astronomers think that the Oort Cloud extends out to a distance of 50,000 astronomical units (1 AU is the distance from the Earth to the Sun), or 1 light-year. In fact, the influence of the Sun’s gravity could extend out to 2 light-years away, the point at which the pull from other stars is stronger.
Surface gravity of the Sun: 27.94 g
Density of the Sun
The density of the Sun is 1.4 grams per cubic centimeter. Just to give you a comparison, the density of water is 1 g/cm3. In other words, if you could find a pool large enough, the Sun would sink down and not float. And this seems kind of counter-intuitive. Isn’t the Sun made of hydrogen and helium, the two lightest elements in the Universe? So how can the density of the Sun be so high?
Well, it all comes down to gravity. But first, let’s calculate the density of the Sun for ourselves.
Formula for density is to divide mass by volume. The mass of the Sun is 2 x 1033 grams, and the volume is 1.41 x 1033 cm3. And so, if you do the math, the density of the Sun works out to be 1.4 g/cm3.
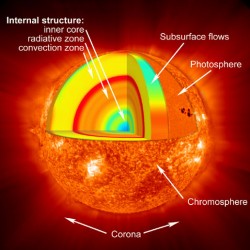
The Sun holds itself together with gravity. Although the outermost layers of the Sun might be less dense, the intense gravity crushes the inner regions to enormous pressures. At the core of the Sun, the pressure is more than 1 million metric tons/cm sq – that’s equivalent to more than 10 billion times the atmosphere of the Earth. And once you get those kinds of pressures, fusion can ignite.
Density of the Sun: 1.622 x 105 kg/m3
Volume of the Sun
The volume of the Sun is 1.412 x 1018 km3. That’s a lot of cubic kilometers. Do you need something to compare this with? The volume of the Sun is so great that it would take 1.3 million planets the size of the Earth to fill it up. Or you could fill it with almost 1000 planets the size of Jupiter.
Volume of the Sun in cubic kilometers: 1.412 x 1018 km3
Volume of the Sun compared to Earth: 1,300,000
Circumference of the Sun
The circumference of the Sun is 4,379,000 km.
Just for comparison, the equatorial circumference of the Earth is 40,075 km. So, the circumference of the Sun is 109 times larger than the circumference of the Earth. And the circumference of the Sun is 9.7 times bigger than the circumference of Jupiter.


Is there a correlation between star mass and and Radii/size(solar radius compares star to the sun. An 1 in solar radii the radius of the sun)?