[/caption]
Many an alternative theory of gravity has been dreamt up in the bath, while waiting for a bus – or maybe over a light beverage or two. These days it’s possible to debunk (or otherwise) your own pet theory by predicting on paper what should happen to an object that is closely orbiting a black hole – and then test those predictions against observations of S2 and perhaps other stars that are closely orbiting our galaxy’s central supermassive black hole – thought to be situated at the radio source Sagittarius A*.
S2, a bright B spectral class star, has been closely observed since 1995 during which time it has completed over one orbit of the black hole, given its orbital period is less than 16 years. S2’s orbital dynamics can be expected to differ from what would be predicted by Kepler’s 3rd law and Newton’s law of gravity, by an amount that is three orders of magnitude greater than the anomalous amount seen in the orbit of Mercury. In both Mercury’s and S2’s cases, these apparently anomalous effects are predicted by Einstein’s theory of general relativity, as a result of the curvature of spacetime caused by a nearby massive object – the Sun in Mercury’s case and the black hole in S2’s case.
S2 travels at an orbital speed of about 5,000 kilometers per second – which is nearly 2% of the speed of light. At the periapsis (closest-in point) of its orbit, it is thought to come within 5 billion kilometres of the Schwarzschild radius of the supermassive blackhole, being the boundary beyond which light can no longer escape – and a point we might loosely regard as the surface of the black hole. The supermassive black hole’s Schwarzschild radius is roughly the distance from the Sun to the orbit of Mercury – and at periapsis, S2 is roughly the same distance away from the black hole as Pluto is from the Sun.
The supermassive black hole is estimated to have a mass of roughly four million solar masses, meaning it may have dined upon several million stars since its formation in the early universe – and meaning that S2 only manages to cling on to existence by virtue of its stupendous orbital speed – which keeps it falling around, rather than falling into, the black hole. For comparison, Pluto stays in orbit around the Sun by maintaining a leisurely orbital speed of nearly 5 kilometers per second.
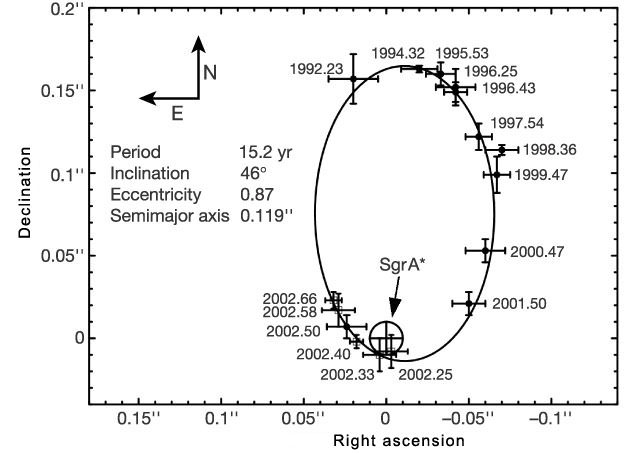
The detailed data set of S2’s astrometric position (right ascension and declination) changes over time – and from there, its radial velocity calculated at different points along its orbit – provides an opportunity to test theoretical predictions against observations.
For example, with these data, it’s possible to track various non-Keplerian and non-Newtonian features of S2’s orbit including:
– the effects of general relativity (from a external frame of reference, clocks slow and lengths contract in stronger gravity fields). These are features expected from orbiting a classic Schwarzschild black hole;
– the quadrapole mass moment (a way of accounting for the fact that the gravitational field of a celestial body may not be quite spherical due to its rotation). These are additional features expected from orbiting a Kerr black hole – i.e. a black hole with spin; and
– dark matter (conventional physics suggests that the galaxy should fly apart given the speed it’s rotating at – leading to the conclusion that there is more mass present than meets the eye).
But hey, that’s just one way of interpreting the data. If you want to test out some alternative theories – like, say Oceanic String Space Theory – well, here’s your chance.
Further reading: Iorio, L. (2010) Long-term classical and general relativistic effects on the radial velocities of the stars orbiting Sgr A*.

