[/caption]
Holographic Dark Information Energy gets my vote for the best mix of arcane theoretical concepts expressed in the shortest number of words – and just to keep it interesting, it’s mostly about entropy.
The second law of thermodynamics requires that the entropy of a closed system cannot decrease. So drop a chunk of ice in a hot bath and the second law requires that the ice melts and the bath water cools – moving the system from a state of thermal disequilibrium (low entropy) towards a state of thermal equilibrium (high entropy). In an isolated system (or an isolated bath) this process can only move in one direction and is irreversible.
A similar idea exists within information theory. Landauer’s principle has it that any logically irreversible manipulation of information, such as erasing one bit of information, equates to an increase in entropy.
So for example, if you keep photocopying the photocopy you just made of an image, the information in that image degrades and is eventually lost. But Landauer’s principle has it that the information is not so much lost, as converted into energy that is dissipated away by the irreversible act of copying a copy.
Translating this thinking into a cosmology, Gough proposes that as the universe expands and density declines, information-rich processes like star formation also decline. Or to put it in more conventional terms – as the universe expands, entropy increases since the energy density of the universe is being steadily dissipated across a greater volume. Also, there are less opportunities for gravity to generate low entropy processes like star formation.
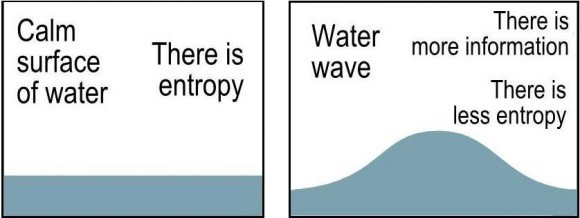
So in an expanding universe there is a loss of information – and by Landauer’s principle this loss of information should release dissipated energy – and Gough claims that this dissipated energy accounts for the dark energy component of the current standard model of universe.
There are rational objections to this proposal. Landauer’s principle is really an expression of entropy in information systems – which can be mathematically modeled as though they were thermodynamic systems. It’s a bold claim to say this has a physical reality and a loss of information actually does release energy – and since Landauer’s principle expresses this as heat energy, wouldn’t it then be detectable (i.e. not dark)?
There is some experimental evidence of information loss releasing energy, but arguably it is just conversion of one form of energy to another – the information loss aspect of it just representing the transition from low to high entropy, as required by the second law of thermodynamics. Gough’s proposal requires that ‘new’ energy is introduced into the universe out of nowhere – although to be fair, that is pretty much what the current mainstream dark energy hypothesis requires as well.
Nonetheless, Gough alleges that the math of information energy does a much better job of accounting for dark energy than the traditional quantum vacuum energy hypothesis which predicts that there should be 120 orders of magnitude more dark energy in the universe than there apparently is.
Gough calculates that the information energy in the current era of the universe should be about 3 times its current mass-energy contents – which closely aligns with the current standard model of 74% dark energy + 26% everything else.
Invoking the holographic principle doesn’t add a lot to the physics of Gough’s argument – presumably it’s in there to make the math easier to manage by removing one dimension. The holographic principle has it that all the information about physical phenomena taking place within a 3D region of space can be contained on a 2D surface bounding that region of space. This, like information theory and entropy, is something that string theorists spend a lot of time grappling with – not that there’s anything wrong with that.
Further reading:
Gough Holographic Dark Information Energy.


This article reminded me of a song by John Lennon called Mind Games, which I copy here for your amusement…
“We’re playing those mind games together,
Pushing barriers, planting seeds,
Playing the mind guerilla,
Chanting the Mantra peace on earth,
We all been playing mind games forever,
Some kinda druid dudes lifting the veil.
Doing the mind guerilla,
Some call it the search for the grail,
Love is the answer and you know that for sure,
Love is flower you got to let it, you got to let it grow,
So keep on playing those mind games together,
Faith in the future outta the now,
You just can’t beat on those mind guerillas,
Absolute elsewhere in the stones of your mind,
Yeah we’re playing those mind games forever,
Projecting our images in space and in time,
Yes is the answer and you know that for sure,
Yes is the surrender you got to let it, you got to let it go,
So keep on playing those mind games together,
Doing the ritual dance in the sun,
Millions of mind guerrillas,
Putting their soul power to the karmic wheel,
Keep on playing those mind games forever,
Raising the spirit of peace and love, not war,
(I want you to make love, not war, I know you’ve heard it before)”
NGC 7635 resembles a jellyfish? composed of stellar stuff….
This article reminded me of a song by John Lennon called Mind Games, which I copy here for your amusement…
“We’re playing those mind games together,
Pushing barriers, planting seeds,
Playing the mind guerilla,
Chanting the Mantra peace on earth,
We all been playing mind games forever,
Some kinda druid dudes lifting the veil.
Doing the mind guerilla,
Some call it the search for the grail,
Love is the answer and you know that for sure,
Love is flower you got to let it, you got to let it grow,
So keep on playing those mind games together,
Faith in the future outta the now,
You just can’t beat on those mind guerillas,
Absolute elsewhere in the stones of your mind,
Yeah we’re playing those mind games forever,
Projecting our images in space and in time,
Yes is the answer and you know that for sure,
Yes is the surrender you got to let it, you got to let it go,
So keep on playing those mind games together,
Doing the ritual dance in the sun,
Millions of mind guerrillas,
Putting their soul power to the karmic wheel,
Keep on playing those mind games forever,
Raising the spirit of peace and love, not war,
(I want you to make love, not war, I know you’ve heard it before)”
NGC 7635 resembles a jellyfish? composed of stellar stuff….
very interesting…we are amused…
Without High Entropy humans would not exist to ponder this conundrum. 🙂
(For fun, here is a hypothetical train of thought)
Sentience reduces entropy by coding higher levels of complexity.
(*1 “The problem of organization in living systems increasing despite the second law is known as the Schrödinger paradox”
One might assume that other sentiences in the universe (should they exist) do the same regardless of biology. Sentience thus might be thought of as an entropy trap, by coding the physical universe into a state of ordered reality or equilibrium.
The one perplexing part is what happens to this encoded information when a person dies. (if anything) Dark energy could be the transmuted sentience ? Thus preserving the second law of Thermodynamics. There is an awful lot of it in Universe however, and its improbable that it all comes from sentience such as humans. That might suggest that all dynamic and complex physical entities in the universe trap entropy. (I mean stars, planets, and life) That this is only released as dark energy when the body dies (Deleted Information). This still does not provide any clues of what Dark energy might be, but if consciousness exists outside the arrow of time, then its likely that any surviving energy might as well.
Alternatively, If we discovered a way to get more negative entropy would we live longer. ? 🙂
Further Reading:
http://en.wikipedia.org/wiki/Emergentism
* 1
http://en.wikipedia.org/wiki/Entropy_and_life
Don’t think this is right – whatever work intelligences put into to organizing and building things requires using up free energy and dissipating waste heat in the process – e.g. we make a big contribution to entropy by digging up fossils fuels and burning them.
In the purely physical world yes, Physicists do rather prefer a more classical definition. 🙂
To quote Schrödinger.
“Let me say first, that if I had been catering for them [physicists] alone I should have let the discussion turn on free energy instead. It is the more familiar notion in this context. But this highly technical term seemed linguistically too near to energy for making the average reader alive to the contrast between the two things”
Im not here to defend the viewpoint, merely to point out that it has been considered before. My own interpretation is an intellectual muse. It cant be proven in any way I can imagine, so its at best a branch of study veering into Philosophy.
Indeed this line of thinking is better expressed in Gibbs Free energy theory. Which is far more consistent with classic notions of Thermodynamics. To quote chemist John Avery;
“The (apparent) paradox between the second law of thermodynamics and the high degree of order and complexity produced by living systems, according to Avery, has its resolution “in the information content of the Gibbs free energy that enters the biosphere from outside sources.”
http://en.wikipedia.org/wiki/Gibbs_free_energy
OK – I don’t have a problem with life and complex systems being free energy ‘traps’. Indeed fossil fuels are a great example of that.
But once you start saying that a complex system can generate more free energy than was originally put into it (“negative entropy”), I think you are entering the world of perpetual motion machines etc.
Did I say that? Sorry I was quoting the concept of Negentropy.
http://en.wikipedia.org/wiki/Negentropy
Which is not a depiction of my belief, simply a facet of Information Theory. As far as I know its not considered a Pseudo science.
I thought it was pertinent to Gough’s interpretation of free energy. Or at least that it presented another viewpoint on the matter.
Im not explaining it very well obviously. Lets move back to the world of Physics.
It is pretty much tied only to pseudoscience, see your own reference (“organization theory”).
Since negentropy doesn’t reflect the actual physics but obfuscates it by replacing actual entropy change with a model of a flow _in the wrong direction_ it has found very little actual use.
Sorry – didn’t mean to imply you personally, just debating the concept.
It isn’t an actual paradox any more than the twin paradox or the EPR paradox, you know: the solution is in the formulation.
Life isn’t very ordered, nor much producing entropy; cell entropy production is bounded by rust from below and methane burning from above. The amount of entropy produced by cell growth is far less than entropy produced by sun light hitting and then dispersing from Earth’s surface.
This is a deepity. That does “coding” mean here?
If you get back to biology, the entropy production from apparent complexity of evolution is order of magnitude less than the entropy production of cell growth; it is ~ 10^-10 of entropy production of sun light.
The rest suggest dualism for no apparent reason. That is not science as we know it.
I just want to say: thanks for the link to that paper, Torbjörn!
I just want to say: thanks for the link to that paper, Torbjörn!
FUCK UR MOM AND SHE FUCKED ME TOOOO
Wow, a discussion about entropy that doesn’t increase the disorder of my stomach! =D
The tie in between the holographic principle and Landauer’s principle is, if not problematic (more below) so the correct way as I understand it.
Gough’s predictions:
————————
I looked briefly on Gough’s work, and while I think it is wrong (more below) we should start out by asking what he predicts and how it connects with earlier theory. Gough connects entropy over Landauer’s principle to energy.
In table 1 Gough (and his 3x prediction) lists several energy contributions from various parts of the universe. We can note that they are roughly the same. I think this is to be expected and can be predicted from standard cosmology.
Gough’s energy contribution term is proportional to an ideal gas law energy term. GR cosmologies are basically looking at matter et cetera components from an ideal gas law model AFAIU, and before inflation the local universe is roughly equilibrated if not in equilibrium from the expansion.
The purpose of inflation is to predict how the observable universe appears so equilibrated, yet admits structure formation from blowing up variations. So Gough’s work is passing a consistency test. But nothing new is predicted.
The same happens for Gough in his figure 1. Given standard cosmology the local structure formation has had to work up energy differences out of the pre-inflationary local homogeneity. [One can well ask about the values of slopes and the coincidence of z ~ 1. But I don’t think Gough answers that, he finds it from fits what I can see. Here other theories like Boussou’s environmental model are predictive.]
Finally Gough presents a distinguishing prediction in his figure 2. His “holographic information energy” model differs to a cosmological constant at low z.
The holographic principle and Gough’s model:
—————————————————–
Note that all these ideas and useful concepts are tied with vague links. If a “deepity” is the attempt to look deep while not being that (Dennett), a “firmity” must be the attempt to look firm despite its absence.
The holographic principle is inspired by the black hole “information” paradox. But the latter isn’t about conservation of algorithmic information at all but the need for unitarity in quantum physics (conservation of probability). Instead the former is, while still lacking a firm definition and model (I think), usually expressed as conservation of degrees of freedom of physical systems.
The connection with this to Landauer’s principle and algorithmic information is interesting and a topic for long discussions in itself. However, what is clear to me is that the Wikipedia reference is using a definition that admits several interpretations.
Looking into Bennett’s paper, the factual description is easier to parse. It is the algorithmic information content in a computer that has degrees of freedom (realized as logic gate “bits”). But the environment accepts entropy increase in many forms, from conversion of electric energy to heat, to degree of freedom dispersal similar to the computer calculating.
At this point we end up with the usual physics of thermodynamics.
By the holographic principle, or just by the conservation of matter-energy within the horizon of the observable universe, unitarity is preserved.
Algorithmic information content is an expression of reversible thermodynamics (reversible calculation), but exactly irreversible thermodynamics (irreversible calculation/memory use) is expressed by entropy instead. And as long as the universe expands, entropy can increase and structure formation (or irreversible calculation) can proceed.
As far as I can see, Gough conflates these two concepts.
I am decreasing entropy by simply thinking about this.
Right?
What is holographic entropy? The author Michael Gough makes a case that the entropy of the universe is comparable to the entropy of the universe at large. This should not be that surprising. The observable universe has a type of event horizon, similar to a black h ole horizon. The one difference is this horizon appears to any observer as what the black hole horizon might appear to an observer inside the black hole looking outwards. The event horizon defines the entropy of the system according to its area. In the case of a black hole the larger the area of the black hole the larger its entropy. A large black hole conceals more microstates than a small one, and where these microstates are all coarse grained into a macrostate defined by the black hole. Something similar happens with cosmologies.
We first have to understand where the cosmological event horizon emerges. It is best to work with the de Sitter spacetime, for this is the operative spacetime for inflation and the current epoch of accelerated expansion. To bring a bit of relativity into this, which I usually avoid, I introduce the metric distance. An infinitesimal distance ds is related to the infinitesimal coordinate distances du, dx, dy, dz, where u plays the role of time as
ds^2 = du^2 – dx^2 – dy^2 – dz^2.
This is just a spacetime version of the Pythagorean theorem. A property of a class of spacetimes is that they are conformally invariant. This is related to conformal invariance in complex variables and is one reason most serious people in general relativity work with complex or spinorial GR. Conformal invariance means the above line element may be rescaled by a factor ?, so that
ds’^2 = ?^2(du^2 – dx^2 – dy^2 – dz^2),
is just a trivial rescaling which does not change things like angle differences. Now we let du = ?^{-1}dt, and the conformal factor is then a time dependent factor we identify as ?^2 = a(t) and we have
ds^2 = dt^2 – a(t)(dx^2 – dy^2 – dz^2).
This is as far as I will go with the GR parts, but it is clear that the scale factor is something which changes the scaling of the spatial part with time.
The a(t) maybe computed from Newtonian mechanics, and where the GR part maybe ignored. This is a sort of energy equation which gives,
(a’/a)^2 = 8??/3 = ?/3
for a’ = da/dt and ? the cosmological constant and ? the quantum vacuum energy density. So this is a first order differential equation of the simplest type, fir
a’ = sqrt{?/3}a
which has an easily found exponential solution
a(t) = a(t_0) exp(t sqrt{?/3}).
It is important to illustrate how a galaxy may be accelerated past the event horizon, but where we may still receive photons from it. As we often do things we consider a Taylor expansion of the a(t) for comparatively small times
a(t) /a(t_0) = 1 + sqrt{?/3}t *****
We then convert the time to a distance ( a radial distance r), which is permissible in this linear approximation t = r/c and we have that
a(r) /a(t_0) = 1 + sqrt{?/3c^2}r
the first (a’/a )^2 = ?/3 is also H^2 = (a’/a )^2 and so
sqrt{?/3c^2}r = Hr.
This is Hubble’s law that he deduced by observational data. Now for hr = v and for v = c it is clear that the radius is r = sqrt{3/?}. Now stick this into equation ***** for t = r/c and you get a(t) /a(t_0) = 2 or z = 1. We observe galaxies now beyond z = 8, and they are moving faster than light and have crossed the event horizon.
Entropy associated with an event horizon is S = k A/4L_p^2, for L_p = sqrt{G?/c^3} = 10^{-33}cm, the Planck length. The area of the event horizon is A = 4?r^2 and entropy of the universe is then
S = 3?kc^3/(G??).
If you devide A = 1.0×10^{56}cm^2 by 4L_p^2 you get around 10^{123} which is the number of qubits in the holographic bound. This defines the holographic bound. In the distant future (about 10^{100} years) when the universe has expanded into a vacuum state this will be the entropy of the universe. The physical universe is less than this, and the physical event horizon is not as far removed as a result. The perturbation of matter and energy in the universe introduces more information which is available. Eventually the universe will decay to the holographic bound. Further the de Sitter vacuum will further decay by a form of Hawking radiation and as time — > ? we have ? — > 0 which results in a divergent entropy result.
The cosmological constant is due to the vacuum state of the universe, plus the matter-energy or information available to an observer. The vacuum structure defines the horizon length for the holographic bound. The upshot then is that holographic dark energy is not then that surprising in the way the author here defines it.
LC
There already is another theory by our team linking dark energy with Landauer’s principle and holography . arXiv:0709.0047 , What you describe here is very similar to our model.
Indeed your paper is remarkably similar to this. The cosmological horizon should be reduced from the Bekenstein or holographic bound. I am not sure about the observational status of z = 1 galaxies. Yet a decent survey with some other ruler measure should hone in on this.
LC
Here is the Paper for reader’s benefit:
http://arxiv.org/pdf/0709.0047