Posted on by Jason Major

“Oddball” Galaxy Contains the Biggest Black Hole Yet

Image of lenticular galaxy NGC 1277 taken with Hubble Space Telescope. (NASA/ESA/Andrew C. Fabian)

It’s thought that at the heart of most if not every spiral galaxy (as well as some dwarf galaxies) there’s a supermassive black hole, by definition containing enormous amounts of mass — hundreds of millions, even billions of times the mass of our Sun packed into an area that would fit inside the orbits of the planets. Even our own galaxy has a central SMBH — called Sgr A*, it has the equivalent of 4.1 million solar masses.

Now, astronomers using the Hobby-Eberly Telescope at The University of Texas at Austin’s McDonald Observatory have identified what appears to be the most massive SMBH ever found, a 17 billion solar mass behemoth residing at the heart of galaxy NGC 1277.

Located 220 million light-years away in the constellation Perseus, NGC 1277 is a lenticular galaxy only a tenth the size of the Milky Way. But somehow it contains the most massive black hole ever discovered, comprising a staggering 14% of the galaxy’s entire mass.

“This is a really oddball galaxy,” said Karl Gebhardt of The University of Texas at Austin, a team member on the research. “It’s almost all black hole. This could be the first object in a new class of galaxy-black hole systems.”

The study was led by Remco van den Bosch, who is now at the Max Planck Institute for Astronomy (MPIA).

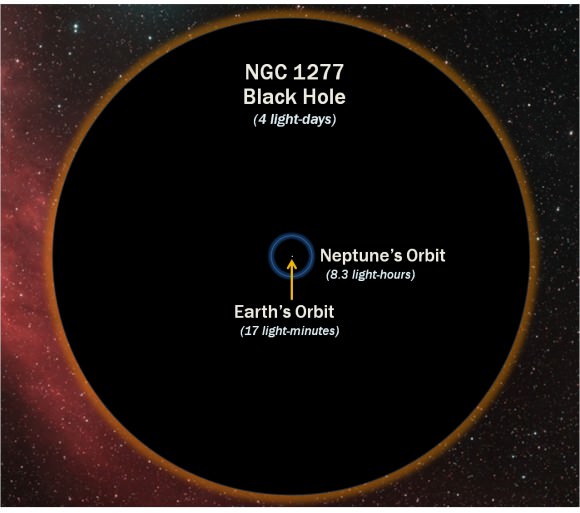
It’s estimated that the size of this SMBH’s event horizon is eleven times the diameter of Neptune’s orbit — an incredible radius of over 300 AU.

How the diamater of the black hole compares with the orbit of Neptune (D. Benningfield/K. Gebhardt/StarDate)

Although previously imaged by the Hubble Space Telescope, NGC 1277’s monster black hole wasn’t identified until the Hobby-Eberly Telescope Massive Galaxy Survey (MGS) set its sights on it during its mission to study the relationship between galaxies and their central black holes. Using the HET data along with Hubble imaging, the survey team calculated the mass of this black hole at 17 billion solar masses.

“The mass of this black hole is much higher than expected,” said Gebhardt, “it leads us to think that very massive galaxies have a different physical process in how their black holes grow.”

To date, the HET team has observed 700 of their 800 target galaxies.

In the video below, Remco van den Bosch describes the discovery of this unusually super supermassive black hole:

Read more on the UT Austin’s McDonald Observatory press release here, or this press release from the Max Planck Institute for Astronomy.

39 Replies to ““Oddball” Galaxy Contains the Biggest Black Hole Yet”

  1. Is this SMBH close enough and it’s event horizon big enough to attempt any direct “imaging” of the EH or accretion disk? If not with current ‘scopes, with some near-future equipment?

    CJSF

  2. THAT’s a black hole!

    “It’s almost all black hole.”

    Fair dinkum? Perhaps as the star’s velocities goes, but not how the hole masses. It’s a beaut with a black hole pimple. But it’s a bottler pimple.

    Now there’s the next boozer, mate?

  3. Find one 100 times heavier and it would have only one gee of freefall acceleration at the event horizon… Incredible. And stars can possibly orbit even this one at highly relativistic velocities without being tidally disturbed…

    600 AU / 50 Mpc = around 10 microarcseconds, it’s nearly the same angular size as Milky Way’s SMBH, so it could be imagined with Event Horizon radio-interferometer, but without much more details than another targets.

    1. The horizon is at R = 2GM/c^2, and the mass of the sun is 2×10^{30}kg. G = 6.67×10^{-11}Nm^2/kg^2 and c = 3×10^8m/sec. The horizon radius is about 3000m. The gravity acceleration a = GM/r^2 = GM/(4GM/c^2)^2 = c^2/(4GM/c^2) = c^2/2R. For the sun the acceleration is about 1.5×10^{13}m/s^2. It is now easy to compute the acceleration at the horizon for any black hole that is N times the mass of the sun. We just divide by N. For a billion solar mass black hole a = 1.5×10^4m/s^2. For this 17 billion solar mass black hole a = 882m/s^2. A 100 times larger black hole a = 8.8m/s^2 which is pretty close to 1-gee on Earth.

      This is one helluva black hole. It makes one wonder how this beast came into existence.

      LC

      2. Yeah but come on that math was obvious, anyone could have done it in their head, you didn’t need to type it out haha

      3. I thought I would complete this discussion by illustrating how this is an approximation of sorts. To really compute this one must use the Killing vector K = K_t with

        g^2 = (1/2)?_aK_b?^aK^b

        where K_t = sqrt{1 – 2m/r). Therefore ?_rK_t = 1/sqrt{1 – 2m/r)m/r^2 and g^{rr}?_r(g^ttK_t} = 1/sqrt{1 – 2m/r)m/r^2, and so

        g = 1/sqrt{1 – 2m/r)m/r^2.

        So technically as r — > 2m it requires an infinite acceleration to remain on the horizon. However, if we are somewhat removed from the horizon we may write this as

        g =~ (1 + m/r)m/r^2 =~ m/r^2 + O(1/r^3).

        So this “back of the envelope calculation” I did earlier assumes this Newtonian limit up to the horizon.

        LC

  6. OK, I’ll reveal my ignorance and ask, why don’t we ever see a black hole as a black hole against a bright background? Or do we, and I’ve missed it? I keep reading about black holes, but I don’t recall ever seeing an obvious image of one. Where is it in the shot above?

    2. They dont emit light in the visible spectrum and all light that gets within the advent horizon is doomed to being pulled in. And since the only way we see things is either by them emitting light or reflecting(which is still emitting) light, we cannot see black holes. Hence the name. And they are so massive that they can bend light around them in a lens like fashion and will distort the view of objects behind them. That is how we typically detect them is by the way they disturb the image of the objects behind them.

      1. They also emit radiation (light), right next to their advent horizon that zing away at nearly light speeds. This has something to do with quantum physics and I do not know much more beyond that. Has something to do with the fact that space isnt empty, but virtual particles pop in and out of existence too. And have a strange tendency to do more so near black holes.

      2. From my limited understanding, particle/antiparticle pairs pop into existence and immediately annihilate each other at an equal rate everywhere in space. The difference at a BH is that one of the members of the pair could happen to be sucked in while the other member is not sucked in to the BH.

        From Wikipedia: Physical insight into the process may be gained by imagining that particle-antiparticle radiation is emitted from just beyond the event horizon. This radiation does not come directly from the black hole itself, but rather is a result of virtual particles being “boosted” by the black hole’s gravitation into becoming real particles.

    4. They’re too small – even this one would only appear 5 microarcseconds across when silhouetted against background stars – you’d need a telescope with 1000 times higher resolution than the highest one that currently exists in order to see it.

    6. Yes, I realised what I was asking later in the day – they’re too small to be seen directly. Even this one, even though bigger than Solar system sized, is still very small at these distances. Must think harder before opening mouth 🙂

  7. May black holes be cleaning-recycling machines providing material for creating parallel universes ?

  10. Maybe in the same class as OJ 287 none the less it is just beyond imagination to think of such massive objects with 600 AU diameter event horizon and just 250 million LY away. It would be great if has become a Quasar to see with in our life time. Hope the 37 Billion solar Mass black hole spotted in 2011 also comes true with more details of it.

  12. Earth’s orbit is 17 light minutes?

    Where have I gone wrong,

    cir = 2 (pi) r = 2*(pi)*(8.3) = 52

    Is there some relativity adjustment I am missing?

    Thanks!

  13. Very interesting subject… All i know is, stay away from ’em.. This one sounds scarier than most….

  16. The article doesn’t mention this, and neither does the Hobby-Eberly telescope website.

    What method are they using to detect these black holes? Since it’s an earth-based telescope, it can’t be by X-ray emissions, and it’s too far away to observe individual stars orbiting it at the center of the galaxy (as far as I know, the only galaxy that we can ever hope to accomplish that is our own anyway). I also expect that it’s pretty much impossible to observe the gravitational lensing effect of a black hole at the center of any galaxy. Observing the radio emissions of a relativistic jet is also out of the question for this visible-light observatory.

    And those are the only methods I know about.

    1. I believe that they can, in fact, measure blue shifts in stars even in such distant galaxies, and from that determine the mass of the black hole they are orbiting.

    1. I did search for the bloody paper at arXiv last night, but it had not been posted at that particular time! Anyway, thanks for finding it.

      1. Many heartfelt thanks for the links you post (and I, for the life of me, can’t seem to locate on my own). I just got lucky this time. 😉

  19. Actually the calculation is wrong, or works for a distance reasonably removed from the event horizon. See above.

    LC

  20. We’re not looking for the circumference, you want the diameter.

    So we have,

    d = cir / (pi) = 52 / (pi) = 16.55 (or 16.66 light minutes, if you didn’t round earlier)

    16.66 light minutes, OR 16 minutes & 40 seconds, sounds a lot like 17 minutes to me.

Comments are closed.