[/caption]
Astronomers generally accept the theory that our universe looks the way it does because of cosmic inflation — rapid expansion in the moments after its birth. This explains the expanse and apparent flat shape of the universe observed through instruments like NASA’s Wilkinson Microwave Anisotropy Probe. But inflation isn’t the only model that explains the early universe. There are others, and they get wacky.
Three physicists from the University at Buffalo — Ghazal Geshnizjani, Will Kinney and Azadeh Moradinezhad Dizgah — set out to investigate other cosmic models. Their study titled “General Conditions for Scale-Invariant Perturbations in an Expanding Universe” appeared in November in the online Journal of Cosmology and Astroparticle Physics (not to be confused with the Journal of Cosmology) and contained some interesting results.
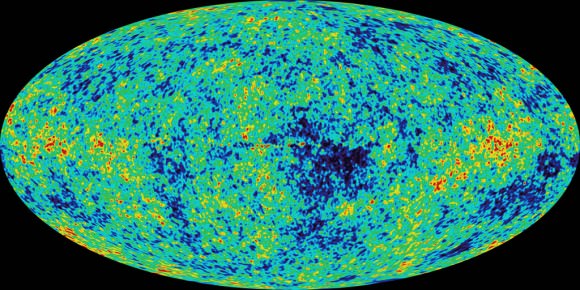
They stuck with the basics — that the theory of gravity is correct and that the early universe did rapidly expand. With these two constraints, the team found that only three models explain the early universe and the distribution of matter we observe today. But these models require very strange physics.
According to their calculations, the early universe required an accelerated cosmic expansion (inflation), a speed of sound faster than the speed of light, or extremely high cosmic energy to end up with our current universe. The third model actually demands such high energy that scientists would need to invoke a theory of quantum gravity like string theory to explain the extra dimensions of space-time that would pop up.
The takeaway message? Inflation turns out to be the only way to explain the universe within the context of standard physics, said Kinney. He allows that someone might come up with exotic physics to explain or create other models, like a speed of sound faster than that of light, but suspects people are more comfortable working with models that fit within commonly accepted laws of particle physics.
The difficulty of explaining other models, said Kinney, “puts the idea of inflation on a much stronger footing, because the available alternatives have problems, or weirdnesses, with them.”
Cosmic inflation incorporates quantum field theory to explain the distribution of matter in the universe. Under normal circumstances, particles of matter and antimatter can pop into existence suddenly before colliding and annihilating each other instantly. These pairs flew apart so rapidly after the universe’s birth that they didn’t have a chance to recombine. The same theory applies to gravitons and antigravitons, which form gravity waves.
These particles of matter are the basis of all structure in the universe today. Tiny fluctuations cause matter to collapse and form stars, planets, and galaxies.
But the hunt for other viable models continues. Kinney for one isn’t finished exploring other theories, including those that rely on superluminal sound speeds. There may yet be some major changes to our understanding of the cosmos.
Source: The University of Buffalo

Ignorant question … wouldn’t Cerenkov radiation prevent matter from moving fast enough to create superluminal sound waves?
There the press release goes into speculative physics. Inflation becomes sensible in quantum field theory, so that step is usually accepted.
That inflation does some kind of “big rip” to sort out matter and antimatter is a large step AFIU. It would result in Alfvén type of cosmologically equi-distributed matter and antimatter volumes that would interact in their interfaces. That is not seen, and also not expected as there are CP parity violations making matter and antimatter on slightly different footing.
The antigraviton stuff is totally speculative, I think. The graviton is its own antiparticle what I know, same as the photon.
The discussion regarding the rapid separation of particles and antiparticles is an unfortunate description of the accepted mechanism for the origin of large scale structure that probably misrepresents what’s actually going on. A similar thing happens when we try to describe what’s actually happening at the event horizon of a black hole to create Hawking radiation — all the popular conceptualizations fall short of giving an accurate picture.
What’s really happening during inflation is that the vacuum fluctuations of all fields in the theory evolve along with the inflating spacetime. They are amplified and stretched to acausal scales because the comoving Hubble radius actually shrinks during inflation. Fluctuations in the inflaton field — the field that provides the energy density to drive the expansion — become physically manifested as perturbations in the curvature once they’ve reached super-horizon scales. But, the key is that *all* field fluctuate — even the gravitational field. These excitations are stretched by inflation to create a large scale spectrum of relic gravitational waves. Current observations (like ESA’s Planck satellite) are in hot pursuit of this gravitational wave signal, because it would provide strong support for an early period of inflationary expansion.
So, it’s not speculation. The theory of quantum fluctuations as the origin of cosmological perturbations that seeded large scale structure is sound and well-tested. The physical interpretation of these fluctuations — as virtual particle loops in a perturbative framework — is perhaps incorrect. It does serve as a popular illustration that is probably close to getting it right.
I sort of let that statement about anti-gravitons fly. The graviton does not have an antiparticle, just as the photon does not have an antiparticle. Photons and gravitons have quantum numbers pertaining to their spin and polarization. They carry no gauge charges, and that is what defines an antiparticle. The gluon, a gauge particle for QCD, carries two color charges for QCD, and thus it does have an antiparticle. The gluon though can’t exist as a bare particle, but only within a quark plasma or vacuum bubble, or as a gluon chain or glue-ball (a plasma of gluons with zero net color charge). A gluon chain can have the same quantum state as a graviton, and in fact in the AdS ~ CFT physics it is a graviton.
LC
I sort of let that statement about anti-gravitons fly. The graviton does not have an antiparticle, just as the photon does not have an antiparticle. Photons and gravitons have quantum numbers pertaining to their spin and polarization. They carry no gauge charges, and that is what defines an antiparticle. The gluon, a gauge particle for QCD, carries two color charges for QCD, and thus it does have an antiparticle. The gluon though can’t exist as a bare particle, but only within a quark plasma or vacuum bubble, or as a gluon chain or glue-ball (a plasma of gluons with zero net color charge). A gluon chain can have the same quantum state as a graviton, and in fact in the AdS ~ CFT physics it is a graviton.
LC
Ouch! Not only is it sound waves in in perfect fluids as a first approximation, there are non-obvious ties between the model and causality:
“Consider a perfect fluid in a Special or General Relativity context, with equation of state p/c2 = wρ relating the pressure p to the energy density ρ.
If w is constant, the speed of sound is given by c_s^2/c^2 =1/c^2 dp/dρ = w , (1) and if w is slowly varying, this is still a good approximation.
Thus one can get c_s^2 > c^2 easily: simply set w > 1 in the macroscopic description, i.e., presume that p/c^2 > ρ > 0. Then the speed of sound cones lie outside the speed of light cones in all directions1 at all events, and fluid waves can propagate at speeds up to and including this superluminal speed of sound. Of course this is far from ordinary matter. It does not accord with anything so far experienced in the real world. But does it cause serious problems in terms of causal violations or Lorentz invariance, considered macroscopically?”
And the paper goes on to argue that the arguments for superluminal signals are wrong. The problem is how to choose the proper frame:
“No physical violation is involved in this aspect of the proposal. Lorentz-invariant theories not only can have, but to model some aspects of reality must have, non-Lorentz-invariant solutions (otherwise normal sound waves would not be
allowed either). The invariance then maps one solution to another different one, rather than to itself. In other observers’ rest frames, in this case, causal limits will again be determined by the speed of sound cone of the fluid rather than the light cone. There is no way to send a signal into one’s past provided no signal, and no observer, travels outside the sound cone, so this cone is itself the causal
limit cone.”
From the conclusion:
“As in the case of varying speed of light theories (see, e.g., Ref. [26] for a discussion), one must take physics as a whole into account whenever proposing theories of superluminal speed of sound; one cannot just tinker with some part of physics without thinking of the consequences for the whole.”
Good question, bad answer.
Can someone tell me,where I can get a complete description of string theory?
Here: String Theory summarized.
Use a search engine.
The following website is a decent overview of the topic
http://www.superstringtheory.com
LC
To Amy Teitel:
I’m sure you meant to say “stars, planets (not planes) and galaxies” didn’t you? Please always check your SPELLING before publishing your articles. I’ve seen this kind of mistake in several of your previous commments and this generates unnecessary confusion among the readers. Thank you.
To Torbjorn Larsson:
I believe that many UniverseToday readers are aware by now that you hold a broad knowledge in astrophysics from your regular comments in this page. However, it would be wise of you just to keep those complicated mathematic equations only to yourself. Most readers certainly enjoy a detailed explanation clarifying the issuein general but couldn’t care less about meaningless abstract equations on and off all the time within the context of your comments. Thank you.
With all due respect, some of us do understand Torbjorn’s equations and appreciate his input. It’s just a shame Disqus doesn’t provide nice formatting for equations.
I’m sure there are plenty of people for whom his posts are too in-depth, but my advice to them would be to skim his posts – not a particularly difficult task for the discerning comment-reader.
If you really do have an issue with his posts, consider reporting them to a moderator – I’m sure the UT staff (which you saw fit to insult for easily-made spelling errors) will be happy to ignore your complaints.
LOL! Love that last sentence!
I disagree with you.
please don’t ask him to be vapid and topical. some people are engaged with the topic and enjoy an in-depth answer.
Junovidor, sigh, in a way, you’re right but you certainly came across as a bit of a blowhard. I can’t read Torbjorn’s equations but I do wish he’d try to make a point with them. As for spelling mistakes, this is a blog. I guess you missed that. Not a published, peer-reviewed text. Take for instance, your spelling of comments…with an extra ‘m’. We all do it. Just takes a slightly more open approach to appreciate the articles notwithstanding.
Hi Peristroika,
The correct spelling of the word comment is with TWO ‘m’ so there’s no extra ‘m’ as you mentioned in your reply. Just check a dictionary for that matter.
Comet is the word with one ‘m’ only and if fits perfectly within the range of the subjects discussed within UniverseToday’s page.
Besides my comments were not intended to offend anyone but rather to call the attention to a couple of things that when happen more often than expected they just divert one’s attention and pleasure from the reading. Anyway, no hard feelings on my side.
Well, maybe I’m seeing double but in your initial comment, there are 3, count ’em, THREE m’s in the word comment in your first paragraph. Just sayin’. No hard feelings!
I disagree,
Torbjorn Larsson and lcrowell’s equations are actually very interesting and adds to the forum. Maybe you are not interested, but that does not mean that everyone is not interested.
I agree with you. Often LC’s and Torbjorn’s math is hard to get my head around, but it is great gray matter exercise trying. Also, when it is over my head, it is very easy to skip past to the explanations. Keep that science stuff coming!
Pointing out errors is cool, but be nice about it. Besides, I don’t think anyone would read ‘planes’, and think “wow there are planes in space??”.
Also, you can do what I do if Torbjorn’s mathematics are too complex for you, and that is skip over his post. I don’t get why you have to go out of your way to make a big deal about it. Besides, I know there are a lot of mathematically inclines readers here.
If these things annoy you, though, you should be aware that your post is way more annoying than anything you mentioned. So, you know, maybe just chill.
Can anyone explain, in a lay-way, how sound waves and speed of sound come into this? I was surprised to see them pop up in this discussion at all!
The universe was very compact back then. So compact that one could regard is as one big solid/fluid/gaseous ball. Matter bumping into each other is basically sound.
One of the interesting things about waves is that although the matter bumping into each other does not violate the speed of light, the wave itself can exceed that speed. (e.g. AC current, the electrons stay in place within the wave and do not really move, but the signal as a wave moves very very fast. The same for water waves. )
An ‘oops’ here…no, waves of all sorts can NOT exceed the speed of light. That would violate the ‘neither matter nor information’ specification in the TofR. Because of electrons inhabiting probabilities, there is the slight possibility of FTL electron placement likelihoods on atoms cruising at near light speeds but no, normally, it jes don’ happen. Anyone else weigh in on how sound gets in here?
It has to be pointed out that inflation does not tell us about the origin of the universe. Inflation occurred at a time when the fabric of spacetime was classical or not quantum mechanical. There was then a prior episode where spacetime itself was quantized in some manner. This prior period is a subject of theoretical research.
The basic equation of cosmology is the Friedmann-Lemaitre-Robertson-Walker (FLRW) equation. This can be understood using Newtonian mechanics and gravity. Some people may object to this as overly mathematical, but if you are to have an interest in astronomy a familiarity with Newtonian mechanics is advised. The second law of mechanics by Newton told us that the force on a body is equal to its mass times the acceleration F = ma. The law of gravity is that the force on a body of mass m by another mass M is
F = -GMm/r^2
which is equal to the force the mass m exerts on the other mass M separated by a radial distance r. So we put them together to get the full equation
mdv/dt = -GMm/r^2
where the acceleration is a = dv/dt — a little differential calculus. The work-energy theorem of elementary physics tells us that the force displaced through a distance is equal to the kinetic energy. So we then write this as ?F•dr, and use dr = (dr/dt)dt (chain rule in calculus) = -vdr (motion is negative r direction = attraction) and get
?vdv = GM?dr/r^2
or with a bit of math:
(1/2)v^2 = GM/r.
We recognize (1/2)v^2 as the “energy per mass” and this equals the change in the potential.
We can convert this equation to a cosmological equation. We consider the distance to a galaxy r = ax, where a is a scale factor which is used to slide the ruler measure x to give a distance r. We then have that all of the dynamics are contained in the scale factor, so v = (da/dt)x, which we write as a’x, the prime denotes a time derivative. The above equation becomes
(a’x)^2 = GM/ax.
The mass M is all of the mass of galaxies in some volume V = (4?/3)r^3 = (4?/3)(ax)^3. So the mass M is equal to the density of mass (mass-energy) in a volume or M = ?V and this equation is then
(a’/a)^2 = 8?G?/3.
This is the FLRW equation for cosmology, where motion of the space is given by a scale factor a, which evolves with time. This is a Hamiltonian (energy equation) which governs dynamics.
The Hamiltonian for the scale factor a in FLRW with general relativity is more generally
(a’/a)^2 = (8?G?/3) – k/a^2,
which has different solutions for different densities ?. The factor – k/a^2 is a curvature term, where k = 1 means the space is a sphere, k = 0 it is flat and infinite, and k = -1 means it is a hyperbolic saddle shape. This leads to a dynamical equation of motion when considered as a Hamiltonian for k = 0
da/dt = sqrt(8?G?/3)a.
For a constant density ? = ?/(8?G), ? the cosmological constant, this reflects some constant mass-energy in the vacuum. This solution is an exponential solution
a ~ exp(sqrt{8?G?/3}t),
which is the inflationary solution. The space expands exponentially with time, which includes an accelerated expansion that also increases. The current state of the universe is of this nature, where there is some dark energy (vacuum energy or quantum zero point energy) which has a larger density than the mass-energy of stuff like galaxies and even dark matter.
The early inflationary period was an epoch with a far larger vacuum energy, as much as 10^{110} times what it currently is. The exponential expansion went through 63 efolds, or for time such that exp(sqrt{8?G?/3}t) ~ e^{63}. This stretched out the space enormously, which means the earlier initial data of the universe prior to inflation are stretched out to huge redshift values.
LC
Great explanation!
Very nice to derive the Friedmann equation using just Newtonian mechanics!
I have some questions:
1) In the “(a’x)^2 = GM/ax.” isn’t a factor of (1/2) at the left missing?
2) What you want to say when you call “Hamiltonian” the equation “(a’/a)^2 = 8?G?/3 “? The equation above does not look like a Hamiltonian function (for all readers: a Hamiltonian function is a function of momentum and position that is equal to the sum of kinetic and potential energy)
3)Dark energy, with its constant energy density in an expanding Universe isn’t the most flagrant violation of conservation of energy?
I did indeed miss a factor of a half, which I changed. This did not affect the rest of the calculation. I also wrote the Hamiltonian explicitly with H = 0.
As for energy violation, this equation has to do with a conservation of energy density. It is also distributed on an infinite space R^3. So the issue of energy conservation is something that is sort of hidden away. Conservation of energy is “funny” in general relativity. It is only explicitly defined if there is a symmetry of the spacetime along the time direction which defines a constant timelike momentum vector. This symmetry is called a Killing vector. Spacetime cosmologies do not explicitly have this. To get into the matter more deeply does require cranking out the curvatures and field equations of general relativity. The stress-energy tensor contains a term ? + p, where the pressure term for the de Sitter spacetime obeys p = -?. This negative pressure can in a sense be thought to remove work, think pdV = NkdT = dS = differential of entropy, which prevents the generation of energy from the constant vacuum energy density under expansion of space.
It is rather remarkable that FLRW spacetime physics can be discussed in a first order model by just using Newtonian mechanics. In fact if Newton had been aware of the expanding universe he could have worked this up.
LC
If conservation laws come from symmetries, like conservation of energy from time “translations” in spacetime (if I understand this right, this mean that the geometry of space does not changes in the timelike direction)…
… and since gravitational interactions are not in general time-symmetric (except special cases like the Minkowski, Scharwrzchild and Kerr spacetimes that does not change in the timelike direction)…
… then in the general case gravity violates conservation of energy?
…and the reason we do not have measured anything like that in the lab or or observed it in the near universe is because the gravitational interaction is very weak and in common astrophysical situations the Scharwzchild solution is an excellent approximation to the gravitational field of stars, planets,etc; and this spacetime does not change with time?
Radial symmetric gravity fields do have timelike isometries or Killing vectors. So black holes and more ordinary gravity fields do conserve energy. Gravity waves manage to also conserve energy. There is a bit of mathematics involved with curvature tensors. The Riemann curvature tensor is the sum of the Weyl curvature and the Ricci curvature. How this sum is done is a bit complicated. The Weyl curvature is a form of curvature which preserves volumes. If you have a sphere in two dimensions that encloses a volume the Weyl curvature is such that as the spacetime evolves, or that points on and inside this sphere moves on some geodesic the sphere may be deformed, but the volume remains constant. Think of there being test masses at every point on the sphere and take the limit the mass goes to zero. The Ricci curvature does not preserve volume. If you put a spherical shell of dust around the Earth, a star or black hole, the dust particles will fall inwards and contract the volume they inscribe.
There is an elegant mathematics developed by Penrose, Petrov and Pirani. The Weyl curvature is a type of operator or machine that acts on Killing vectors to give eigenvalues. The algebra of this system describes the PPP system of spacetime types. Some of these solution types are the D-types for black holes, the I, II, and III types (Robinson-Trautman spaces) and type N spaces for gravity waves. This physically may be thought of as the near field term, the black hole, the far field term as gravity waves and intermediary symmetries. This is comparable to the near and far field solutions to Maxwell’s equations.
Cosmologies describe the expansion of space, so if you placed a spherical shell of dust particles in a cosmology that are not gravitationally bound to each other that shell will expand its volume. So there is no Weyl curvature which gives a timelike isometry. With a spherical symmetric gravity, say a black hole, the solution is defined by regions that do not enclose the mass. This is similar in technique to using Gaussian surfaces in electromagnetism.
Symmetry is important in defining a conserved quantity. Emmy Noether worked a general theorem for this early last century. In classical mechanics momentum may be thought of as the generator of a position change. If the space has homogeneous symmetry so it has no distinguishing properties from point to point momentum is conserved. The same holds with time, if time translations are invariant under rescaling or reparameterization then energy is conserved. If the space is isotropic under rotations then angular momentum is conserved. These define conjugate pairs of observables or variables:
x p
t E
? J
which in classical mechanics defines Poisson bracket structures and in a quantized setting the commutators of variables which give their uncertainty relationships.
LC
What about:
1) a group of massive and dense objects bound by gravity, like a stellar cluster or two black holes orbiting each other?
2) micro black holes resulting from particle colliders (or cosmic rays)?
3)An accreting black hole (the mass is increasing, so the hole is growing with time)?
4)A small evaporating black hole (near the end of its life) that is shrinking rapidly?
In those cases does not the spacetime is NOT time-invariant, so energy isn’t conserved, or I am missing something?
In those cases mass-energy is probably conserved, though these systems have less symmetry to work with so it is hard to define an ADM mass. A system of two black holes in an orbit is not integrable, and only approximately so if the two black holes are far apart and the system approaches a near Newtonian situation. Two tightly orbiting black holes will produce gravity waves and this is more complex than a Newtonian two-body system that is integrable. In Newtonian mechanics n-body systems for n > 2 are not solvable in closed form, and in general relativity systems are not generally integrable for n > 1. One has to use perturbation methods (parameterized post-Newtonian) or numerics in order to approximate these systems.
Quantum black holes likely also conserve mass-energy, though this system is only understood with classical back reactions used to treat the black hole. A fully quantum mechanical or quantum field theoretic treatment of black holes that are a few Planck masses is a fascinating topic in conjunction with string theory and quantum information. I will bow out of discussing that here, for that is a very deep and abstract subject. Quantum black holes which are thought to be maybe produced in the LHC, are not really black holes. They are QCD systems with certain correspondences with AdS-Schwarzschild spacetimes. This means gluon chains or quark-gluon plasmas can have small quantum amplitudes which correspond to black holes. The LHC can’t produce a real certified black hole, and all the flapdoodle last decade over this was ridiculous nonsense.
LC
“Under normal circumstances, particles of matter and antimatter can pop into existence suddenly before colliding and annihilating each other instantly”
As implied here, the Universe seems to do everything in balance, therefore I would expect an equal number of matter and anti-matter particles forming. Yet as I understand it, the theory to explain why our Universe exists as is would require extra normal matter being formed. This imbalance just doesn’t seem right, but where could the remainder of the anti-matter have gone? Could there be an anti-matter universe out there somewhere?
human also have trillion of cells and chromosomes of different variations
imagine how we’re small in this universe and multiply it by 10 to the power billion so many zeros