[/caption]
There’s a line out of an early episode of The Big Bang Theory series, where Gravity Probe B is described as having seen ‘glimpses’ of Einstein’s predicted frame-dragging effect. In reality, it is not entirely clear that the experiment was able to definitively distinguish a frame-dragging effect from a background noise created by some exceedingly minor aberrations in its detection system.
Whether or not this counts as a glimpse – frame-dragging (the alleged last untested prediction of general relativity) and Gravity Probe B have become linked in the public consciousness. So here’s a quick primer on what Gravity Probe B may or may not have glimpsed.
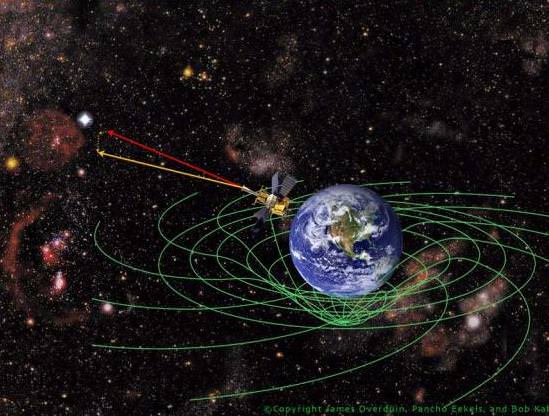
The Gravity Probe B satellite was launched in 2004 and set into a 650 kilometer altitude polar orbit around the Earth with four spherical gyroscopes spinning within it. The experimental design proposed that in the absence of space-time curvature or frame-dragging, these gyroscopes moving in a free fall orbit should spin with their axis of rotation unerringly aligned with a distant reference point (in this case, the star IM Pegasi).
To avoid any electromagnetic interference from the Earth’s magnetic field, the gyroscopes were housed within a lead-lined thermos flask – the shell of which was filled with liquid helium. This shielded the instruments from external magnetic interference and the cold enabled superconductance within the detectors designed to monitor the gyroscopes’ spin.
Slowly leaking helium from the flask was also used as a propellant. To ensure the gyroscopes remained in free fall in the event that the satellite encountered any atmospheric drag – the satellite could make minute trajectory adjustments, essentially flying itself around the gyroscopes to ensure they never came in to contact with the sides of their containers.
Now, although the gyroscopes were in free fall – it was a free fall going around and around a space-time warping planet. A gyroscope moving at a constant velocity in fairly empty space is also in a ‘weightless’ free fall – and such a gyroscope could be expected to spin indefinitely about its axis, without that axis ever shifting. Similarly, under Newton’s interpretation of gravity – being a force acting at a distance between massive objects – there is no reason why the spin axis of a gyroscope in a free fall orbit should shift either.
But for a gyroscope moving in Einstein’s interpretation of a steeply curved space-time surrounding a planet, its spin axis should ‘lean over’ into the slope of space-time. So over one full orbit of the Earth, the spin axis will end up pointing in a slightly different direction than the direction it started from – see the animation at the end of this clip. This is called the geodetic effect – and Gravity Probe B did effectively demonstrate this effect’s existence to within only a 0.5% likelihood that the data was showing a null effect.
But, not only is Earth a massive space-time curving object, it also rotates. This rotation should, theoretically, create a drag on the space-time that the Earth is embedded within. So, this frame-dragging should tug something that’s in orbit forward in the direction of the Earth’s rotation.
Where the geodetic effect shifts a polar-orbiting gyroscope’s spin axis in a latitudinal direction – frame-dragging (also known as the Lense-Thirring effect), should shift it in a longitudinal direction.

And here is where Gravity Probe B didn’t quite deliver. The geodetic effect was found to shift the gyroscopes spin axis by 6,606 milliarcseconds per year, while the frame-dragging effect was expected to shift it by 41 milliarcseconds per year. This much smaller effect has been difficult to distinguish from a background noise arising from minute imperfections existing within the gyroscopes themselves. Two key problems were apparently a changing polhode path and larger than expected manifestation of a Newtonian gyro torque – or let’s just say that despite best efforts, the gyroscopes still wobbled a bit.
There is ongoing work to laboriously extract the expected data of interest from the noisy data record, via a number of assumptions which might yet be subject to further debate. A 2009 report boldly claimed that the frame-dragging effect is now plainly visible in the processed data – although the likelihood that the data represents a null effect is elsewhere reported at 15%. So maybe glimpsed is a better description for now.
Incidentally, Gravity Probe A was launched back in 1976 – and in a two hour orbit effectively confirmed Einstein’s redshift prediction to within 1.4 parts in 10,000. Or let’s just say that it showed that a clock at 10,000 km altitude was found to run significantly faster than a clock on the ground.
Further reading: The Gravity Probe B experiment in a nutshell.

The precession rate is given by
d@/dt = (2GM/rc^2)(freq/5)
or a fifth of the rotational velocity times the Schwarzschild factor. For Earth the Schwarzschild factor is a pretty small ~ 1.5e^{-9}. This results in about 10^{-4} arc-sec per day.
Now if this were put in orbit around Jupiter, with about 300 times the mass and a fast rotation you would get a better signal. Of course better still would be the sun. Yet around Jupiter the precession would be about 10^{-1}arc-sec/day.
LC
Hi, Lawrence, as I am not an Astro-Physicist I can only guess, that the experiment proved (given all challenges, technical and scientific) that AE was right, once again…
IKE
Well it should. Unfortunately it appears the gyroscope has a noise level which makes it hard to get a signal. Maybe the noise can be characterized sufficiently well to filter it out. This is rather disappointing.
The Lense-Thirring effect is due to a magnetic analogue in gravity. So a verification of this is analogous to the Faraday law. This was stated as the “final” test, but in reality a better final test is for gravity waves.
LC
Yes – agree. I don’t know why frame-dragging is considered a ‘final test’ when gravity waves are yet to be detected.
Thanks for the update! As I remember it, Gravity Probe B tests of frame dragging was supposed to hang on further data processing. A preliminary result that promises future sufficient confirmation is then a step forward. Especially since I don’t believe that another such probe will be launched anytime soon.
Btw, where did “final” come from!? Frame dragging is fundamental to be sure, but agreed, gravity waves are more the top of the classical edifice.
Would it be correct to characterize ‘frame dragging’ as a ‘redshift-like’ property of gravitational interaction with space-time ?
I’m not aware that it is ever stated like that. As LC noted above, it’s more commonly discussed as an analogue to magnetism. A orbiting spacecraft is pulled forward in the direction of a planet’s spin as a consequence of its proximity to the planet.
You get redshift when light loses energy moving upwards away from a massive object (for example).
BTW, saying ‘gravitational interaction with space-time’ doesn’t really make sense. Under general relativity, gravity is a consequence of curved space-time – it does not exist independently of it. Mass is what curves/interacts with space-time.
Pretty ‘dicey’ results here… Are there any plans afoot to improve the design and try again?
The general theory of relativity may be written in a series expansion. The terms are in various orders of metric corrections. The fancy version of this is called the parameterized post-Newtonian (PPN) relativity. The second order corrections are similar to the Faraday equation. If you take a spherical charge distribution you get a dipole magnetic field, with the north and south poles at the axis of rotation. On the plane through the equator of the spinning charge these magnetic field lines are perpendicular to that plane. The Lorentz force F = qcxB tells you that a charge moving perpendicular to the field lines experiences a force perpendicular to the field lines and the velocity of the charge. The Lense-Thirring effect is identical in its formalism.
A test charge which approaches the larger spinning charge along a radial direction will experience a force that is in the direction of the tangent velocity of the surface of the spinning charge. So the charge gets pulled along in that direction. The analogue to general relativity carries over. A particle which radially approaches a gravitating body with a large angular momentum will experience a frame dragging in the direction of that rotation.
The Gravity B probe measures this with a rotating gyroscope. The angular momentum of any particle in the gyroscope is given by L = rxP, and one must sum this up to get L = I*angular velocity, I = moment of inertia. This Lense-Thirring effect results in a precession of the gyroscope. Gravity is however a very weak force, and these effects subtle.
LC
I have often wondered, why the “bowling ball on a sheet” depiction of the gravity well, as pictured here is always used. Is it just illustrative because the complete spherical warp cannot be coherently drawn? I haven’t found a description of the physical gyro orientations on the spacecraft on the web but, I assume the polar orbit was chosen to be able to “differentiate” the effect of drag (gyro yaw/precession) being stronger at the plane of rotation and weaker as it approaches the poles.
Now, if indeed we slide down the well at “all” of the infinite vector approaches to the massive body center, it seems a geodetic pitch effect could not be detected (or differentiated) between the plane and the poles, right? This science stuff hurts my head.
Sorry Gravity Probe B. Better luck next time. Go Gravity Probe C! Anyway at least you found the Geodetic Effect. Maybe next time use cube shaped gyros lol jk.