Astronomy is a discipline pursued at a distance. And yet, actually measuring that last word — distance — can be incredibly tricky, even if we set our sights as nearby as the Moon.
But now astronomers from the University of Antioquia, Colombia, have devised a clever method that allows citizen scientists to measure the Moon’s distance with only their digital camera and smartphone.
“Today a plethora of advanced and accessible technological devices such as smartphones, tablets, digital cameras and precise clocks, is opening a new door to the realm of ‘do-it-yourself-science’ and from there to the possibility of measuring the local Universe by oneself,” writes lead author Jorge Zuluaga in his recently submitted paper.
While ancient astronomers devised clever methods to measure the local Universe, it took nearly two millennia before we finally perfected the distance to the Moon. Now, we can bounce powerful lasers off the mirrors placed on the Lunar surface by the Apollo Astronauts. The amount of time it takes for the laser beam to return to Earth gives an incredibly precise measurement of the Moon’s distance, within a few centimeters.
But this modern technique is “far from the realm and technological capacities of amateur astronomers and nonscientist citizens,” writes Zuluaga. In order to bring the local Universe into the hands of citizen scientists, Zuluaga and colleagues have devised an easy method to measure the distance to the Moon.
The trick is in observing how the apparent size of the Moon changes with time.
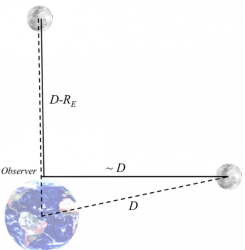
Image Credit: Zuluaga et al.
While the Moon might seem larger, and therefore closer, when it’s on the horizon than when it’s in the sky — it’s actually the opposite. The distance from the Moon to any observer on Earth decreases as the Moon rises in the sky. It’s more distant when it’s on the horizon than when it’s at the Zenith. Note: the Moon’s distance to the center of the Earth remains approximately constant throughout the night.
The direct consequence of this is that the angular size of the moon is larger — by as much as 1.7 percent — when it’s at the Zenith than when it’s on the horizon. While this change is far too small for our eyes to detect, most modern personal cameras have now reached the resolution capable of capturing the difference.
So with a good camera, a smart phone and a little trig you can measure the distance to the Moon yourself. Here’s how:
1.) Step outside on a clear night when there’s a full Moon. Set your camera up on a tripod, pointing at the Moon.
2.) With every image of the Moon you’ll need to know the Moon’s approximate elevation. Most smartphones have various apps that allow you to measure the camera’s angle based on the tilt of the phone. By aligning the phone with the camera you can measure the elevation of the Moon accurately.
3.) For every image you’ll need to measure the apparent diameter of the Moon in pixels, seeing an increase as the Moon rises higher in the sky.
4.) Lastly, the Moon’s distance can be measured from only two images (of course the more images the better you beat down any error) using this relatively simple equation:
where d(t) is the distance from the Moon to your location on Earth, RE is the radius of the Earth, ht(t) is the elevation of the Moon for your second image, α(t)
is the relative apparent size of the Moon, or the apparent size of the Moon in your second image divided by the initial apparent size of the Moon in your first image and ht,0 is the initial elevation of the Moon for your first image.
So with a few pictures and a little math, you can measure the distance to the Moon.
“Our aim here is not to provide an improved measurement of a well-known astronomical quantity, but rather to demonstrate how the public could be engaged in scientific endeavors and how using simple instrumentation and readily available technological devices such as smartphones and digital cameras, any person can measure the local Universe as ancient astronomers did,” writes Zuluaga.
The paper has been submitted to the American Journal of Physics and is available for download here.


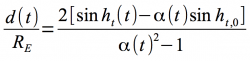
The Moon often appears flattened and distorted when it is near the horizon. I wonder if it is best to avoid shots at this time.
This article as presented here is too simplified and somewhat misleading. Based on Hall’s article, I thought that this might make for a doable exercise for students in an introduction to astronomy course. I then went and downloaded the original paper, which I recommend to those who are interested. While this experiment is doable by a “citizen scientist,” it is definitely not for casual observers. The process outlined in the paper is not without complexity, both procedurally and mathematically. Significant planning is required. Further, Hall leaves out the need for a DSLR (digital SLR camera). The paper’s authors use a Canon T3i (an excellent intro DSLR used by many astrophotographers). However, such a camera costs $600-$700, which puts this experiment beyond the means of many. (DSLRs can record the pixel size of the image, which point-and-shoot digicams typically do not.) Also, unless you have a long enough zoom lens for your DSLR (another cost factor), you will need to attach it to a telescope (as did the paper’s authors) in order to get a reasonably sized image. This requires a T-ring and T-mount (not expensive, but this adds to the complexity of the project). I appreciate and applaud the desire to make astronomical content accessible for a wide audience, but articles of this type need to be more up front about the requisite equipment and skill levels needed.
That’s an excellent analysis. I got my hopes up after reading the title of the article, hoping to incorporate this into some type of high school-level laboratory activity. But it seems far, far more complex than that.
A simpler way to do this (but less accurate) would be to use parallax. Students group up into threes and on a clear night they all go to different latitudes but within the same approximate longitude. Since the moon is so close, they may not need to go very far… one person stays in town, one goes 30 miles north, the other 30 miles south. Using cell phones, coordinate the time each will take a measurement of the angle the moon is in the sky from the southern horizon (if in the northern hemisphere). They each should have subtly different angles. Using the gps function on the cell phones, each student needs to record their exact gps coordinates from where they took the measurement so that the students can easily calculate how far apart they were. Now using simple trigonometry, you should be able to calculate the distance to the moon. You could do this with just two students as well. No cameras necessary. With some free astro apps, I bet those apps will tell you the angle the moon is in the sky just based on your gps coordinates. Might be a good group science homework exercise.
Determining the distance of the Moon was one of the practical exercises set by the late Prof. Archie Roy to the first-year astronomy class at Glasgow University in 1963-64. We all had to match the apparent diameter of the Moon to a disc of fixed size slid along a metre stick, noting the distance at which they matched, and keep doing it for 7-8 months. We then averaged the greatest and least diameters for each month, and calculated the distance. When the distances were averaged, they came to 55 Earth radii rather than 60 – but no advanced digital cameras were needed!